1. 引言
数字在人类的生活中起着非常关键的作用,而人们则依靠数量的基本直觉来指导各种各样的日常决策。例如,在超市,我们不需要明确地计算排队的人数就能识别出哪个收银员所在的队伍最长。这种直觉也被称为“数感”,它植根于一种非语言的数字表征系统 [1] [2],是一种具有种系进化基础的认知系统,允许个体不依赖符号知识对视觉、听觉或跨通道呈现的实物或实物记号的数量刺激进行表征和运算。具体表现为数量2可以表示为两个圆点(:),两根木棒(II),并且这种表征方式是人类与动物所共享的,并在不同的文化中广泛使用的 [3]。而与动物不同的是,人类拥有一套正式的数学系统来补充他们的数感。这种系统依赖于符号知识对数字和数词等形式的数量进行表征 [4]。具体表现为“2”、“二”、“Ⅱ”,“贰”等,这种表征方式是人类所特有的、受文化教育影响的抽象数量表征 [5]。
近年来,随着科学的发展和实验技术的改进,关于数字加工的研究也越来越多,其中备受关注的是Dehaene等人提出的空间数字反应联合编码效应(Spatial Numerical Association of Response Codes, SNARC),即被试在对数字进行大小判断时,对小数按左键反应快,对大数按右键反应快的现象 [6]。这一效应的发现为数空表征提供了强有力的依据,也成为了研究数空关系的重要方式。
SNARC效应被发现之后,研究者们开展了大量的关于SNARC效应的研究,最初研究主要集中于符号数字。Hung等人使用阿拉伯数字和两种不同的汉语数字(一,壹)为实验材料测试了SNARC效应,结果发现阿拉伯数字和简单汉语数字有从左到右的SNARC效应,而复杂汉语数字没有这种效应。他们认为没有发现复杂的汉语数字的影响,可能是因为不经常使用 [7]。Kopiske等人也使用了阿拉伯数字、简单的汉语数字和汉语手语数字为刺激材料测试了被试的SNARC效应。他们发现阿拉伯数字有明显的SNARC效应,简单的中国数字有较弱的SNARC效应,但没有证据表明手语数字有SNARC效应 [8]。
有研究者考虑到数量不仅可以通过阿拉伯数字来表达,而且也可以通过其他表征形式来传达,例如罗马符号、中文数字词、手指、圆点图案、算盘珠子等。因此,非符号数量是否在空间进行表征的问题就自然而然地产生了。Nuerk等人采用数字和点阵为刺激进行数字奇偶判断任务,结果发现两者都出现了SNARC效应,但数字的反应速度比点阵快 [9]。胡林成等人使用数字和圆面积为材料对儿童进行了大小比较任务,结果发现了圆面积的SNARC效应,而不存在数字的SNARC效应 [10]。Nemeh等人同样使用了大小比较任务,结果出现了点阵SNARC效应 [11]。
从以往研究中可以看出不同数量表征形式会对数空联结产生影响,那么不同的数量形式之间是共享性还是特异性表征呢?研究者也关注到了这个问题并提出了不同的理论模型。其中单一表征模型(Unique-representation View)认为,近似数量系统(Approximate Number System, ANS)是算术能力的基础,个体对不同形式的数量进行表征时都会激活该系统,即符号和非符号具有相同的表征基础 [12]。而双重表征模型(Dual-representation View)则认为,不同形式的数量依赖于不同的表征系统,且各系统之间不存在重叠表征,并明确指出非符号数量表征与近似数量表征系统相联系,符号数量表征与精确数量表征系统相联系。综合以上分析发现关于符号和非符号数量表征的共享和特异性问题还没有得到解决,需要更多的证据澄清二者之间的关系。
在当前的研究中,我们设计了两个实验来探究符号和非符号的表征问题。从数量空间表征的角度出发,若符号和非符号是共享的表征,那么数字和圆面积混合的实验条件下进行的大小比较相比于单纯的数字大小比较任务增加了非符号圆刺激,该条件下的SNARC效应量要大于单纯数字大小比较条件下的SNARC效应量。若符号和非符号是特异性表征,那么圆面积的增加不会对数字的SNARC效应产生任何影响,两种实验条件下的SNARC效应量也不会有显著差异。本研究选择大学生作为被试是因为实验的目的是探究符号和非符号的共享和特异性表征问题,相比于儿童和青少年,成年被试各方面发展趋于稳定,选择其作为被试可以避免由于发展中个体本身生理的不成熟因素给实验带来的影响。
2. 实验一 数字大小比较
2.1. 被试
30名师范大学学生自愿参加了实验,其中男性15人,女性15人,视力或矫正视力正常,此前均未参加过类似实验,实验结束后支付10元人民币作为报酬。
2.2. 实验材料与仪器
实验材料是黑色的数字(1~9,不包括5),屏幕上呈现的Arial字体,数字字号大小36。实验皆在安静明亮的实验室中由Lenovo电脑完成,显示器为14寸彩色液晶显示器,分辨率为1024 × 768。实验程序由Eprime2.0软件编制,反应键为标准键盘上的F和J键,被试双眼与屏幕中心处于同一水平,距离屏幕约60 cm。
2.3. 实验设计与程序
实验采用2 × 2被试内实验设计,自变量为数字大小(小数:1、2、3、4;大数:6、7、8、9)和反应位置(左;右),因变量为反应时。
实验流程如图1所示,实验要求被试对数字的大小进行判断。实验开始后,首先出现注视点“+”1000 ms,之后呈现刺激1500 ms,被试需要又快又准确地做进行判断并反应,随后出现空屏1000 ms,接着进入下一试次。对每个被试的左右手反应都进行平衡,即一半的试次要求被试F键对小于5的数字反应,用J键对大于5的数字反应,另一半试次则相反。实验共分为2个block,分别为左手对小数反应、右手对大数反应的block 和右手对小数反应、左手对大数反应的block。每个block中每个数字随机呈现8次,即每个block有64个trial,整个实验大概持续10分钟,为防止被试出现疲劳,block间隙时被试可以根据自己的状态适当休息。
2.4. 数据处理
采用统计软件包SPSS 25.0对所获得的数据进行统计处理。实验的数据分析包括以下部分:1) 计算每个被试在所有实验条件下的平均反应时。2) 检验SNARC效应。采用Dehaene等人 [6] 的方法,对数据进行2 (反应位置:左、右) × 2 (数字大小:大、小)重复测量方差分析,以初步检验是否存在SNARC效应。若交互作用显著,说明大数和小数在左右反应位置上的反应时有差异。3) 检验SNARC效应的效应量大小和方向。回归分析检验SNARC效应的方法是由Fias等人在Lorch与Myers [13] 提出的方法基础上改进而来,他认为回归分析用来检验SNARC效应更为敏感 [12],目前这种方法广泛应用在SNARC效应的研究中。具体步骤如下:分别计算每个被试对每个数字的右手平均反应时和左手平均反应时,右手和左手的平均反应时之差dRT作为因变量,将1~9 (不包括5) 8个数字作为自变量进行回归分析,并将回归方程的斜率与0进行t检验,如果差异显著并且斜率为负,则证明表现出了经典水平方向的SNARC效应,即左侧对小数反应更快,右侧对大数反应更快。
2.5. 实验结果
因一名被试正确率低于90%,故而将其剔除,共29名被试纳入统计,反应的错误率为2.61%。因为总体错误率很低,所以本实验以及后续实验没有对错误率进行进一步分析。删除错误反应的反应时数据以及2.5个标准差之外的极端值。计算被试左右键在两种数量表征条件下各自对于小数(1~4)和大数(6~9)反应的平反应时和标准差,描述统计结见表1。

Table 1. Average response time and standard deviation under each experimental condition (ms)
表1. 各实验条件下平均反应时和标准差(ms)
进行两因素重复测量方差分析,结果表明发现,数字大小和反应位置的交互效应显著F(1, 28) = 13.23,p = 0.001,η2 = 0.32,简单效应分析结果表明,不同反应位置对小数的反应时差异不显著,而对大数的反应时差异显著,F(1, 28) = 16.96,p < 0.000,左侧对大数(M = 507.59)的反应时显著慢于右侧(M = 499.13)。方差分析结果显示,存在数字SNARC效应。
继续采用回归分析的方法进一步讨论SNARC效应。回归分析结果见图2,回归方程为L1:dRT = 19.99 − 4.98 × 数字,回归斜率与0差异显著,t(28) = −4.02,p < 0.000,结果见图3。回归分析结果进一步表明,被试对数字表现出了SNARC效应,左侧对小数的反应快于右侧,右侧对大数的反应快于左侧;而对点阵没有表现出SNARC效应。
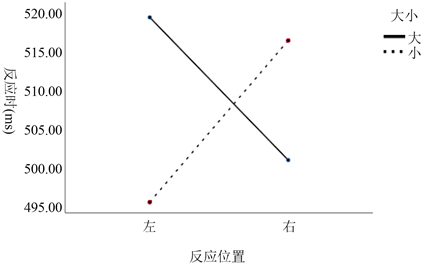
Figure 3. The interaction between reaction position and number size under number conditions
图3. 数字条件下反应位置与数字大小的交互作用
3. 实验二 数字面积混合条件下的数字大小比较
3.1. 被试
32名师范大学学生自愿参加了实验,其中男性16人,女性16人,视力或矫正视力正常,此前均未参加过类似实验,实验结束后支付10元人民币作为报酬。
3.2. 实验材料与仪器
实验材料是黑色的数字(1~9,不包括5)和圆(半径为1~9,不包括5)混合在一起组成的复合刺激,如 。实验皆在安静明亮的实验室中由Lenovo电脑完成,显示器为14寸彩色液晶显示器,分辨率为1024 × 768。实验程序由Eprime2.0软件编制,反应键为标准键盘上的F和J键,被试双眼与屏幕中心处于同一水平,距离屏幕约60 cm。
。实验皆在安静明亮的实验室中由Lenovo电脑完成,显示器为14寸彩色液晶显示器,分辨率为1024 × 768。实验程序由Eprime2.0软件编制,反应键为标准键盘上的F和J键,被试双眼与屏幕中心处于同一水平,距离屏幕约60 cm。
3.3. 实验设计与程序
实验采用2 × 2的被试内实验设计,自变量为数字大小(小数:1、2、3、4;大数:6、7、8、9)和反应位置(左;右),因变量为反应时。
实验流程如图4所示,实验要求被试对数字的大小进行判断。实验开始后,首先出现注视点“+”1000 ms,之后呈现刺激1500 ms,被试需要又快又准确地进行判断并反应,随后出现空屏1000 ms,接着进入下一试次。对每个被试的左右手反应都进行平衡,即一半的试次要求被试F键对小于5的数字反应,用J键对大于5的数字反应,另一半试次则相反。实验共分为2个block,分别为左手对小数反应、右手对大数反应的block和右手对小数反应、左手对大数反应的block。每个block中每个数字随机呈现8次,即每个block有64个trial,整个实验大概持续10分钟,为防止被试出现疲劳,block间隙时被试可以根据自己的状态适当休息。
3.4. 数据处理
同实验一。
3.5. 实验结果
因1名被试正确率低于90%,故而将其剔除,共31名被试纳入统计。被试反应的错误率为2.38%。去除掉错误反应的反应时数据,再删除2.5个标准差之外的极端值。计算被试左右键在两种数量表征条件下各自对于小数(1~4)和大数(6~9)反应的平均反应时和标准差,描述统计结果见表2。

Table 2. Average response time and standard deviation under each experimental condition (ms)
表2. 各实验条件下平均反应时和标准差(ms)
进行两因素重复测量方差分析,结果表明,数量大小和反应位置交互作用显著,F(1, 31) = 29.95,p < 0.000,η2 = 0.491,见图5。简单效应分析结果表明,不同反应位置不仅对小数的反应时差异显著,F(1, 31) = 33.65,p < 0.000,而且对大数的反应时差异也显著,F(1, 31) = 15.14,p < 0.000,左侧对大数(M = 574.51)的反应时显著慢于右侧(M = 512.14),左侧对小数(M = 495.24)的反应时显著快于右侧(M = 570.77)。数量大小的反应时差异不仅在左侧显著,F(1, 31) = 22.88,p < 0.000,而且在右侧也显著,F(1, 31) = 26.22,p < 0.000,在左侧,小数的反应时(M = 495.24)显著快于大数(M = 574.51),在右侧,大数的反应时(M = 512.14)显著快于小数(M = 570.77)。方差分析结果显示,在数字面积混合的实验条件下也存在数字SNARC效应。
继续采用回归分析的方法进一步讨论数字面积混合情况下的数字SNARC效应。回归方程为L2:dRT = 65.14 − 12.99 × 数字,回归斜率与0差异显著,t(30) = −2.73,p = 0.01,结果见图6。回归分析结果进一步表明,被试对数字表现出了SNARC效应,左侧对小数的反应快于右侧,右侧对大数的反应快于左侧。
比较L1和L2两个回归方程的回归系数,来探究被试在不同实验条件下产生的SNARC效应的效应量是否存在差异,结果发现二者差异未达到显著,t(58) = 0.449,p = 0.655。表明两种实验条件下的SNARC效应量大小不存在显著差异。

Figure 5. The interaction between the response position and the size of the number
图5. 反应位置与数字大小的交互作用
4. 讨论
在本研究中,我们发现被试在两种实验条件下都表现出了数字SNARC效应,经回归分析比较,单纯数字和数字面积混合条件下SNARC效应量差异不显著。研究中没有任何证据表明非符号圆面积促进数字SNARC效应的效应量,加快数字SNARC效应的反应速度。对于圆面积和数字的空间表征之间没有产生相互影响的结果,说明两种数量表征形式具有不同的神经处理基制,即特异性表征。
这个解释可以得到行为研究结果的支持。从以往众多关于SNARC效应的研究中发现符号和非符号SNARC效应的许多重要特征存在差异。阅读方向的改变不会引起非符号SNARC效应方向的改变,但会改变符号SNARC效应的方向。任务的灵活表达方式(用“更多”或“更少”来表示)能改变非符号SNARC效应的方向,却不能影响符号SNARC效应的方向。具体来说,用“更多”的指导语指示被试做任务,会得到从左到右的非符号SNARC效应,而用“更少”的指导语则会引起非符号SNARC效应的方向反转。但是需要注意的是,这些任务略有不同,对于非符号刺激,两个刺激同时可见,而在符号SNARC任务中,数字通常一次显示一个。此外,非符号刺激形式中常见的指导语为多/少,并不符合符号SNARC任务的大/小,因此任务设置中的这些差异确实使比较不完美。尽管如此,目前观察到的行为差异确实表明了两种数量形式的表征差异。
这个解释也可以得到神经成像研究结果的支持 [14] [15] [16] [17] [18]。Holloway等人发现,被试进行符号数量判断时左角回和颞上回有更多激活,而在非符号数量判断任务中,右后上顶叶有更多激活 [14]。Bulthé等人运用多体素模式分析发现,符号数量加工中,未在任何感兴趣区发现距离效应,而非符号数量加工中,在大多数脑区均出现显著的距离效应,如左顶内沟前部、右额上回、右顶上叶等 [16]。Peters等人发现,儿童进行符号减法算术任务时,角回和缘上回有显著的激活,而在非符号减法算术任务种,枕叶中部和顶上叶以及额上回和脑岛有更多的激活 [18]。
关于符号和非符号数量信息空间表征的差异性问题,我们的证据也不是结论性的,但有助于确定这个问题,为符号和非符号特异性表征提供了直接的行为证据。接下来,需要进一步从不同的角度出发,设计更有效的实验,选择敏感的工具继续推进当前的研究成果。
5. 结论
1) 数字面积混合实验条件下存在数字SNARC效应。
2) 单纯数字和面积数字混合两种实验条件下的SNARC效应量之间不存在显著差异。
3) 符号和非符号数量空间表征存在特异性。
参考文献