基于GM灰色系统模型的浙江省人均GDP预测

Forecast of Per Capita GDP in Zhejiang Province Based on GM Grey System Model

摘要: 人均GDP是经济学中衡量人均产出的一个有效统计量，它可以在很大程度上度量社会中居民福利状况，能够指导政府部门做出一系列经济决策。本文基于灰色系统理论，根据2000~2019年浙江省人均GDP数据建立GM(1,1)模型与GM(2,1)模型，结果显示模型精度良好。根据建立的模型对浙江省2020~2025年人均GDP进行预测，为浙江省制定经济政策提供理论依据。

Abstract: Per capita GDP is an effective statistic to measure per capita output in economics. It can measure the welfare status of residents in society to a large extent, and can guide government departments to make a series of economic decisions. Based on the grey system theory, this paper establishes the GM(1,1) model and GM(2,1) model based on the per capita GDP data of Zhejiang Province from 2000 to 2019, and the results show that the model accuracy is good. According to the established model, the per capita GDP of Zhejiang Province in 2020~2025 is predicted, which provides a theoretical basis for formulating economic policies in Zhejiang Province.

1. 引言

GDP (国内生产总值)，反映某地区在一定时间内所生产的最终产品的价值总和，是宏观经济核算的关键指标。2020年，中国国内生产总值首次突破100万亿元大关，这标志着我国改革开放四十余年经济发展取得了显著的成就。总量来看我国已稳居世界第二并预期在不远的将来可以超过美国，人均GDP在过去两年也都突破一万美元，这些已经取得的经济发展数据都表明我们已经实现全面小康水平，但必须要认识到我国距离社会主义现代化强国的目标还有一定的距离。一般认为人均GDP 2万美元是发达国家的最低门槛，3万美元到6万美元为中等发达国家，8万美元以上为高等发达国家，可以清楚看到我国人均经济量距离发达国家还相去甚远。因此对人均GDP进行预测在当下可能比预测总量更为重要，我们是否能够如期完成“十四五”规划和2035远景目标都与人均GDP这个指标密切相关。而浙江省一直都是我国经济强省，民营经济发展水平极高，2020年浙江省GDP总量为64,613亿元，在全国排名第四。而人均GDP金额为110,450元，在全国排名第五。浙江省产业结构等较为合理绿色发展水平较高，可以为我国部分北方省份的发展提供经验，本文所分析的浙江省人均GDP发展对于为我国下一阶段经济建设建言献策意义非凡。

2. 文献综述

GDP作为国民经济运行的一项核心指标，对其进行较为精确的预测对于指导建立预算等有很大的意义。随着实证研究的兴起和预测信息技术的发展，不同研究者分别利用很多不同的模型对我国或各地区GDP数据进行过预测。例如李娜，薛俊强(2013)利用ARIMA模型GDP增长进行预测研究，结果表明2009~2011年GDP预测误差很低，证明了ARIMA模型预测的优良性 [1]；朱青，周石鹏提出LSTM-XGBoost二维组合模型对GDP增速进行预测，并验证了其可靠性 [2]。而近年来越来越多的研究人员尝试利用灰色预测模型对GDP进行预测。王美娜，杨孝斌(2021)选取贵州省2012~2018年数据套用GM(1,1)模型进行预测，并用2019年数据来检验误差，同时通过灰色关联分析方法来考察GDP数据与贵州省产业结构之间的关系。得到了一系列有用的结论 [3]。卢俊岚，王明辉(2019)用灰色预测模型对广东省1978至2016年GDP进行分析，并预测2017年之后的数据，在套用原始数据时进行了对数化处理，得到了较高准确度的预测结果 [4]。赵国君，张星(2018)对GM(1,1)模型进行了优化改进，对初始条件和背景值都做出了调整得到了较高的精确度，据此得出结论认为北京市未来几年GDP年均增长率将保持在9.30%左右 [5]。祖培福，赵文英等(2018)利用背景值优化后的GM(1,1)模型预测牡丹江未来GDP数据，同时对优化后和传统模型之间进行了对比，发现优化模型得出结果更科学并为牡丹江的发展提出建议 [6]。田梓辰，刘淼(2018)在GM(1,1)模型的基础上通过拉格朗日插值和改进的拉格朗日插值对其背景值做了重构，对新疆近年GDP数据进行了分析预测 [7]。

3. 模型构建与数据来源

3.1. 模型原理概述

上世纪80年代，为解决小样本，信息缺乏下的模型构建问题，邓聚龙教授首次提出了灰色理论 [8]。从本质上看，灰色系统模型是一种指数函数模型，其主要是将随机性较强的原始序列进行数据处理，使其变得光滑呈指数型，增强其规律性，然后建立模型预测，基于这一逻辑对信息不完全下的系统进行拟合预测，其特有的优势为解决原始数据样本量小，影响因素极多等难以进行的研究提供了有效的解决方案。目前灰色模型已经被广泛应用于我国各产业的众多领域，已然解决了社会生产生活中的大量问题。

本文将分别采用GM(1,1)模型通解、GM(1,1)模型邓聚龙解和GM(2,1)模型的优化解三种算法对浙江省人均GDP数据进行预测 [9]。

3.1.1. GM(1,1)模型通解

GM(1,1)模型是最简单的灰色系统模型，其基础是常微分方程的解析解，GM(1,1)微分方程直接求解的建立过程如下：

假设有一个变量 $x\left(t\right)$ 是时间变量t的函数，它满足一阶常微分方程条件：

$\frac{\text{d}x\left(t\right)}{\text{d}t}+ax\left(t\right)=b$ (1)

这里，参数a和b是两个常系数。假设参数C是任意常数，那么，该微分方程的解析解或者通解为：

$x\left(t\right)=\frac{b+{\text{e}}^{a(C-t)}}{a}$ (2)

如果 $x\left(t\right)$ 有一个初值，在 $t=0$ 时，初值为 $x\left(0\right)$，那么， $x\left(0\right)$ 也满足这个解，因此，参数C满足关系式：

${\text{e}}^{aC}=ax\left(0\right)-b$ (3)

代入微分方程的通解，就有：

$x\left(t\right)=\frac{b}{a}+\left(x\left(0\right)-\frac{b}{a}\right){\text{e}}^{-at}$ (4)

该函数具有指数函数的特征，由于其对于参数a和b的依赖性很强，而参数a和b又是未知的，且在正常情况下不易估计，因此，该模型也被称为灰色系统。由于只有一个变量 $x\left(t\right)$，且是一阶微分，所以记为GM(1,1)。

3.1.2. GM(1,1)模型邓聚龙解

设原始数据离散序列为

$x^{(0)}=\left\{x_0^{\left(0\right)},x_1^{\left(0\right)},\cdots ,x_{n-1}^{\left(0\right)}\right\}\left(n\ge 3;x_k^{\left(0\right)}\ge 0;k=0,1,\cdots ,n-1\right)$ (5)

一次累加后得到如下序列：

$x^{(1)}=\left\{x_0^{\left(1\right)},x_1^{\left(1\right)},\cdots ,x_{n-1}^{\left(1\right)}\right\}\left(n\ge 3;x_k^{\left(1\right)}\ge x_{k-1}^{\left(1\right)};k=1,2,\cdots ,n-1\right)$ (6)

$x_k^{\left(1\right)}={\displaystyle {\sum }_{i=0}^k{x}_i^{\left(0\right)}}\left(i=0,1,\cdots ,k\right)$ (7)

生成 $x^{(1)}$ 的近邻均值等权序列：

$z^{(1)}=\left\{z_1^{\left(1\right)},z_2^{\left(1\right)},\cdots ,z_{n-1}^{\left(1\right)}\right\}\left(n\ge 3;k=1,2,\cdots ,n-1\right)$ (8)

$z_k^{\left(1\right)}=\frac{1}{2}\left(x_k^{\left(1\right)}+x_{k-1}^{\left(1\right)}\right)$ (9)

一阶微分方程求解过程转化如下：

$\frac{\text{d}{x}^{(1)}\left(t\right)}{\text{d}t}+a{x}^{(0)}\left(t\right)=b$ (10)

其中：a，b为待定参数，然后运用最小二乘法求解可得

${\left(a,b\right)}^{\text{T}}={\left(B^{\text{T}}B\right)}^{-1}{B}^{\text{T}}{Y}_N$ (11)

$B=\left[\begin{array}{cc}-z_1^{\left(1\right)}& 1\\ -z_2^{\left(1\right)}& 1\\ \cdots & \cdots \\ -z_{n-1}^{\left(1\right)}& 1\end{array}\right],Y_N=\left[\begin{array}{c}{x}_1^{\left(0\right)}\\ x_2^{\left(0\right)}\\ \cdots \\ x_{n-1}^{\left(0\right)}\end{array}\right]$ (12)

求解a，b后，进而得出方程的时间响应式

${\hat{x}}_k^{\left(1\right)}=\left(x_1^{\left(0\right)}-\frac{b}{a}\right){\text{e}}^{-a(k-1)}+\frac{b}{a}$ (13)

${\hat{x}}_k^{\left(0\right)}={\hat{x}}_k^{\left(1\right)}-{\hat{x}}_{k-1}^{\left(1\right)}$ (14)

3.1.3. GM(2,1)模型的优化解

GM(2,1)和GM(1,1)的区别在于GM(2,1)是二阶常微分方程，GM(1,1)为一阶常微分方程，GM(2,1)微分方程模型建立过程如下：

假设变量 $x\left(t\right)$ 是关于时间t的二阶常微分方程的解，满足条件：

$\frac{{\text{d}}^{2}x\left(t\right)}{\text{d}{t}^2}+a\frac{\text{d}x\left(t\right)}{\text{d}t}+bx\left(t\right)=0$ (15)

则该微分方程的通解为：

$x\left(t\right)=C_1{\text{e}}^{\frac{\left(-a-\sqrt{a^2-4b}\right)t}{2}}+C_2{\text{e}}^{\frac{\left(-a+\sqrt{a^2-4b}\right)t}{2}}$ (16)

为了编程方便，我们对该关系式予以简化：

$x\left(t\right)=C_1{\text{e}}^{mt}+C_2{\text{e}}^{nt}$ (17)

这里，存在关系式：

$m=\frac{-a-\sqrt{a^2-4b}}{2}$ (18)

$n=\frac{-a+\sqrt{a^2-4b}}{2}$ (19)

$C_1=\frac{x\left(0\right){\text{e}}^n-x\left(1\right)}{{\text{e}}^n-{\text{e}}^m}$ (20)

$C_2=\frac{x\left(1\right)-x\left(0\right){\text{e}}^n}{{\text{e}}^n-{\text{e}}^m}$ (21)

3.2. 数据来源

为了研究浙江省人均GDP的增长情况，本文以浙江省统计年鉴为数据选取依据，将2000年至2019年浙江省人均GDP作为原始数据，测算2020年至2025年江省人均GDP。具体指标如表1所示。

Table 1. Per capita GDP data of Zhejiang province

表1. 浙江省人均GDP数据

数据来源：浙江省2000年~2019年统计年鉴。

4. 模型分析

4.1. GM(1,1)模型通解

对于GM(1,1)模型而言，由于其具有指数函数特点，且只有a，b两个参数，适用于最小二乘法，本文运用python中的Curve-Fit函数进行拟合求解，上表为GM(1,1)的具体预测结果。由于在预测时，进行了5次拟合，各拟合结果相关参数如表2所示。

Table 2. Data fitting parameter table of GM(1,1) model

表2. GM(1,1)模型通解数据拟合参数表

尽管进行了5次拟合，但实际上可以发现，a、b两个参数数值基本相等。R²通常用于判断模型的拟合程度，其取值范围为[0, 1]。一般来说，R²越大，表示模型拟合效果越好。本次拟合的误差判定项在小数点后6位也都保持一致，从第七位起才稍有差别，其中R²保持在0.96033左右，拟合效果较为良好。这一现象说明，运用GM(1,1)通解拟合，虽每次拟合都选取了不同的随机初数，但拟合结果都收敛到了相同的值。

将上a，b值代入方程，可得：

$x\left(t\right)=33150.67-19689.67{\text{e}}^{0.06t}$ (22)

拟合效果如图1所示。

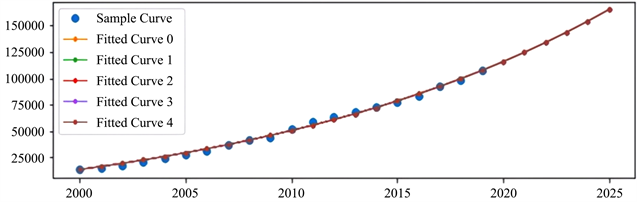
Figure 1. General solution data fitting renderings of GM(1,1) model (Unit: Yuan). Data source: Statistical Yearbook of Zhejiang Province (2001~2019)

图1. GM(1,1)模型通解数据拟合效果图(单位：元)。数据来源：浙江省2001年~2019年统计年鉴

由图可以发现，浙江省未来人均GDP呈明显上升趋势，预计2025年人均GDP将大幅超过15万元，依照现有对于发达国家人均GDP2万美元的标准，浙江省即将步入发达国家的经济发展水平，拟合结果的具体数值如表3所示。

Table 3. GM(1,1) model general solution data fitting effect numerical table

表3. GM(1,1)模型通解数据拟合效果数值表

数据来源：浙江省2000年~2019年统计年鉴。

对拟合具体数据研究发现，5组参数取值下的预测值之间的差异极小，考虑到本文所拟合的数据单位为元，可以基本上判定拟合效果整体表现良好。各年预测值与实际值较为贴近，2020年至2025年各年预测值分别为115,774元、124,573元、133,886元、143,742元、154,173元和165,212元，对于2020年的预测值，结合最新发布的2020年各省人均GDP数据对比发现，2020年浙江省实际人均GDP为110,450元，预测值相较于实际值超出4.6%，但考虑到2020年受疫情影响，全国经济遭受冲击，预测值稍高也处于可接受范围内。结合前文对于浙江省经济发展水平预测及当前汇率水平，可以进一步预测，浙江省将于2021年或2022年步入发达国家经济发展水平。

4.2. GM(1,1)模型邓聚龙解

邓聚龙解是将原来离散序列 $x^{(0)}$ 的一阶微分方程的求解过程转化成了对其一次累加序列 $x^{(1)}$ 和 $x^{(0)}$ 的一阶微分方程，从而最终通过线性代数来求解的一个线性矩阵方程，获得参数 $\left(a,b\right)$ 的估计值。本文仅运用邓聚龙解拟合一次，其参数为 $\left[a,b\right]=\left[-0.094,19009.6147\right]$。这与采用通解算的参数值完全不同，两者不同的主要原因有两方面，一是算法不同，通解所采用的为最小二乘法，而邓聚龙解采用的是线性矩阵乘法；二是样本不同，通解所计算的为原始数据样本，而邓聚龙解所计算的是经过处理后的一次累加序列样本。邓聚龙解的误差项分别为： $R^2=0.9403760$， $R=0.9697299$， $\text{Adj}{R}^2=0.9370636$， $SER=5902.2325548$， $RMSE=5599.3494459$。从R²来看，拟合度较高，结合各项参数，该模型为：

${\hat{x}}_k^{\left(1\right)}=\left(215690.944\right){\text{e}}^{0.094(k-1)}+202229.944$ (23)

${\hat{x}}_k^{\left(0\right)}={\hat{x}}_k^{\left(1\right)}-{\hat{x}}_{k-1}^{\left(1\right)}$ (24)

拟合效果如图2所示。

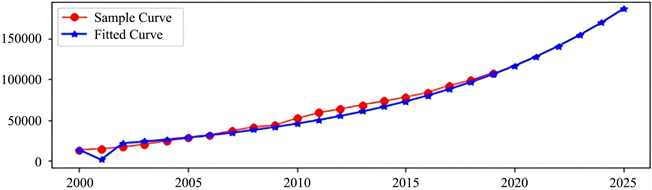
Figure 2. GM(1,1) model Deng Julong data fitting renderings (Unit: Yuan). Data source: Statistical Yearbook of Zhejiang Province (2001~2019)

图2. GM(1,1)模型邓聚龙解数据拟合效果图(单位：元)。数据来源：浙江省2001年~2019年统计年鉴

对比图1可以发现，邓聚龙解下的人均GDP上升幅度明显大于通解下的人均GDP上涨幅度，曲线斜率逐渐变大。两者的拟合效果也有些许区别，对比下，邓聚龙解的离散程度更高，其中2001年有一明显下降，2010年至2015年拟合值也小幅偏离实际值，2001年相差较大主要是由于其通过间接处理原始样本数据的一次累加序列求解所导致，属于算法因素，拟合的具体数值如表4所示。

Table 4. Numerical table of fitting effect of GM(1,1) model Deng Julong solution data

表4. GM(1,1)模型邓聚龙解数据拟合效果数值表

数据来源：浙江省2000年~2019年统计年鉴。

2020年至2025年各年预测值分别为116,023元、127,455元、140,014元、153,810元、168,965元和185,614元，2020年相较于实际值超出5.04%，也处于可接受范围内。但相较于通解的各年预测值，邓聚龙解分别超过了0.22%，2.31%，4.58%，7.00%，9.59%和12.35%，其预测值上涨幅度呈现明显上升趋势，同时在通解的预测值已经较为符合实际值的情况下，邓聚龙解在长期预测下就稍显得偏离实际。故此邓聚龙解相较于通解，更适合对短期数据进行预测。

4.3. GM(2,1)模型的优化解

对于GM(2,1)模型，有4个中间参数m，K，C₁，C₂和2个目标参数a，b，故此，不同初始条件下参数的收敛问题就显得尤为重要，本文在对2000年至2019年数据进行测算时发现，GM(2,1)模型在这一样本量下R²达到1.1789，拟合出现错误，参数结果如表5所示。

Table 5. Parameter values of GM(2,1) model are shown in Table 1

表5. GM(2,1)模型参数数值表一

数据来源：浙江省2000年~2019年统计年鉴。

为了使用GM(2,1)模型对人均GDP数据进行预测，本文选择扩大样本量，选择浙江省1950年至2019年数据重新进行测算，指标回归正常，参数结果如表6所示。

Table 6. Parameter values of GM(2,1) model are shown in Table 2

表6. GM(2,1)模型参数数值表二

数据来源：浙江省统计年鉴。

通过Curve-Fit函数得到的20组拟合参数发现，目标参数a，b完全不能收敛到同一组值，类似的m参数的取值也不同。但是，参数k，C₁，C₂在20组中有17组保持一致，另外3组也相应的保持一致，说明尽管a，b，m不是收敛的，但k，C₁，C₂的值是收敛的。以第一次拟合结果为例，模型的相关系数R²为0.9634，拟合度相较于小样本情况下有明显改善，拟合效果良好， $a=16898.7845$， $b=-1757.9029$， $m=-16898.8886$， $n=0.104$， $C_1=-5.3179$， $C_2=88.3179$，具体模型如下：

$x\left(t\right)=-5.3179{\text{e}}^{-16898.8886t}+88.3179{\text{e}}^{0.104t}$ (25)

拟合效果如图3所示。

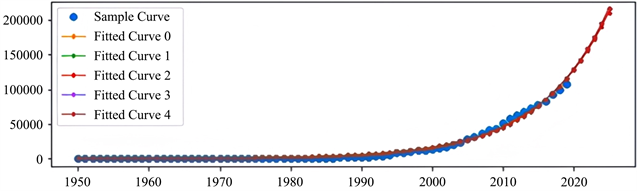
Figure 3. GM(2,1) model optimization data fitting renderings (Unit: Yuan). Data source: Statistical Yearbook of Zhejiang Province (2001~2019)

图3. GM(2,1)模型的优化解数据拟合效果图(单位：元)。数据来源：浙江省统计年鉴

与另外两者模型的预测结果相似，二阶灰色预测函数下的浙江省人均GDP也呈现逐年上涨趋势，但上涨幅度在三个模型中是最高的，其具体拟合值如表7所示。

Table 7. Numerical table of fitting effect of GM(2,1) model’s optimal solution data

表7. GM(2,1)模型的优化解数据拟合效果数值表

数据来源：浙江省统计年鉴。

2020年至2025年各年预测值分别为128,370元、142,443元、158,059元、175,386元、194,613元和215,948元，在各年预测数据中，2015年及以前，基本呈现实际值大于预测值，在2016年以后，开始呈现预测值大于实际值，2020年对比实际值110,450元超出16.22%，且自2016年起，预测值的偏离度在逐年上升，但考虑到所选样本自1950年开始，期间经历了改革开放等重大战略转型，对经济发展产生极大影响。同时预测值在1995至2019年这25年期间，与预测值的差距在10%上下浮动，长期来看，仍是属于较为可靠的，但短期波动相较于前文两种模型，更为显著。

5. 预测结果总结

对比三个模型的拟合可以发现，小样本数据更适合采用GM(1,1)通解与邓聚龙解来进行测算，同时，对于短期测算，通解与邓聚龙解均可使用，但随着测算时间的延长，邓聚龙解相较于通解会出现预测值增长幅度大幅提升的现象。因此，在中期测算方面，更适合采用GM(1,1)来进行预测。对于拥有大样本容量的情况下，可以采用GM(2,1)模型优化解来进行测算，同时，该模型也更适合长期预测，短期预测过程中的波动性太大。

由于对比后发现，在现有样本量及预测时间长度下，GM(1,1)通解模型的相关性更好，误差更小，图形拟合效果也更好，预测值更加符合实际情况。故本文选择GM(1,1)通解的拟合值作为最终预测值，即：2020年至2025年各年预测值分别为115,774元、124,573元、133,886元、143,742元、154,173元和165,212元。结果显示未来浙江省人均GDP将保持稳步增长，但各年人均GDP增长幅度从7.6%下降至7.16%，增长速度有微弱的减缓趋势。因此，本文得出结论，在当前新发展格局下，经济增长正从高速发展转向高质量发展，尽管浙江省人均GDP总体呈增长趋势，但是值得注意和警示的是在增长的背后却表现出增长放慢的迹象，如何保持住或提升浙江省人均GDP的增长速度才是我们当前最应该思考的问题。

6. 政策建议

6.1. 着眼区域优势资源，构建有特色的产业结构

浙江省取得如此改革成就的原因有很多，产业结构是其中关键因素之一。作为沿海省份浙江省港务航运业十分发达，舟山港货物吞吐量多年居全球第一。此外浙江丘陵地形较多，农业发展相对不具有优势。这使得越来越多的人转而从事商品贸易，义务小商品城享誉海内外。而互联网经济兴起以来，浙江更是在这方面卓有成就，阿里巴巴自身且由其带动的诸多平台经济商家以及直播平台等如雨后春笋般在杭州等地成长，杭州已经成为了互联网经济发展最为靠前的城市之一。义务小商品城、桐庐快递业产业集群以及横店影视城这些都是浙江省取得如此傲人发展成绩的秘诀所在，其他省份应该从中汲取经验。

6.2. 落实“三农”政策，高效促进乡村振兴

实现现代化强国的伟大目标，最大的短板和最深厚的潜力都是在农村。事实上我国已经有相当一部分城市的发展即使进行国际比较也不落下风，比如厦门市人均GDP已经达到两万美元，这已经是发达国家水平。但是我国最广大的农村地区还面临着发展问题，这也是我们提出不平衡的发展这一论述的原因之一，因此要实现更高质量的发展有效提高人均GDP水平，必须切实关注农村地区始终把“三农问题”作为政府工作的重中之重。

6.3. 鼓励创新创业，落实创新驱动发展战略

我国经济总量和人均量都得到了快速的发展，类似高铁、航空航天和工程建设等很多产业也位居世界前列，但还必须注意的是很多关键核心技术还掌握在欧美发达国家手中，诸多种种都成为了我国现阶段发展的卡脖子难题。想要克服受制于人的局面我们必须把创新提到很重要的位置，十八大就以提出：“科技创新是提高社会生产力和综合国力的战略支撑，必须摆在国家发展全局的核心位置。”实际上国家和地方也已经为促进创新做出了很大的努力，我国税法对于研发支出的加计扣除标准也从50%提到75%再提高至100%，我国各大中企业每年的R&D支出也连年上升，这都说明整个社会已经意识到了研发的重要性。但仍要矢志不渝推动创新，我国各省区市之间发展的不平衡在很大意义上就是创新导致的差距，东北地区经济衰落也在于其不能合乎时宜地进行产业转型，振兴东北实际上也在于通过创新这一突破口找到新的发展路径。

致谢

在此本文向所有给予本文帮助的老师同学以最诚挚的感谢，特别是厦门国家会计学院信息管理处的阎虎勤老师，感谢阎老师对我们论文撰写的辛勤指导！此外，也向对本文发表提供帮助的大米(厦门)科技股份有限公司给予感谢。

基金项目

本论文得到了厦门国家会计学院“云顶课题：python财务数据分析”项目和大米(厦门)科技股份有限公司的支持。