1. 引言
理想条件下,扬声器可以近似看成点声源,不具有指向性,将多个扬声器按照一定的空间顺序排列,就形成了扬声器阵列,新的阵列声源具有一定的指向性 [1]。若给每个阵元增加一个延时相位器,就得到了相位补偿阵列,即相控阵;调整阵元的延时量可控制声源波束的传播方向 [2]。相控阵技术最先应用在天线扫频上,通过改变天线的初相位来控制整个阵列的发射角度 [3]。利用同样的思想,将电磁波的频率降低,在超声波阵列或频率更低的声阵列相邻阵元增加相移或者时延,可以控制阵列波束偏转 [4]。早在上世纪30年代,Wolfe和Malter就在JASA上对阵列声源的特性进行了研究 [5]。后来有很多专家学者对相控阵扬声器阵列进行研究,但是由于实验较为复杂,要求较高,研究只停留在仿真阶段。在一些特殊军事环境下的有源降噪问题,如水下潜艇的主动声隐身问题,噪声往往是斜入射的,最有效的方法就是根据噪声的入射方向进行噪声控制,这就需要一个具有可控指向性的声源 [6]。参量阵扬声器也是具有可控强指向性的声源,理论上可以作为有源噪声控制的控制声源 [7] [8] [9]。然而参量阵声源的原波频率较高,而能量转化率较低,实际上很难作为潜艇外敷设的大功率换能器来使用 [10]。
针对这一问题,本文利用相控阵的原理,以线型扬声器阵列和平面矩形扬声器阵列作为研究对象,采用计算机仿真和大量实验测试结果对比的方法,系统性研究扬声器阵列的参数对形成的指向性波束的影响,以获得具有可控强指向性的大功率声源。
2. 相控阵指向性模型和偏转理论
扬声器阵列的排列和阵元的激励不同,产生的指向性会有所不同 [11]。本文研究的扬声器阵列为等幅值激励等间距的扬声器阵列。扬声器排列成阵列后,空间中一点会受到阵列内所有扬声器的影响,由于该点到每个扬声器的距离不同,所以受到的影响也是不同的。当声波的频率相同,相位差固定时,声波产生了干涉叠加 [12]。在空间上任意一点的声压均为各扬声器产生声压的总和 [13],声压函数表示为:
(1)
式中,A为扬声器的激励值,r为测量点到阵列中心的距离,n为扬声器的个数,ω为声波的频率,k = ω/c = 2π/λ,δ = d/2 × sinα,c为声速,λ为在该频率下的声波波长,d为扬声器的间距,α为声阵列轴向与测量点的夹角。
设扬声器阵列的波束指向性函数Dα为线型扬声器阵列夹角为α的某点声压p(α)与扬声器阵列轴向的最大声压p(0˚)之比 [14],则:
(2)
给每个阵元增加一个时延信号Δt改变其产生波形的初相位,进而产生步进相位使波束偏转。线型扬声器阵列和平面矩形扬声器阵列都可以通过改变每个扬声器的初相位使每个扬声器产生的声波同时到达空间中的一个虚拟平面——波阵面,使所有阵元信号在波阵面上实现同相,即实现了波阵面的偏转 [15]。如图1所示,当波束偏转角为θ,相邻阵元所需的波程差l = d × sinθ,设θ0 表示未发生偏转时波束指向性最大的方向,那么相邻阵元的相位差为Δφ = l/λ ,时延信号Δt = d × sinθ/c 。此时带有偏转的指向性函数为 [16]:
(3)

Figure 1. Diagram of linear array directivity deflection
图1. 线型扬声器阵列指向性偏转示意图
阵元个数为M × N 的平面矩形扬声器阵列可以视为M个阵元个数为N的线型扬声器阵列平行排列而成,即平面矩形扬声器是由M个具有相同排列结构的子阵列,子阵中又由N个相同阵元构成,所以线型阵列的性质同样适用于平面矩形扬声器阵列,复合阵的指向性函数满足乘积定理 [17],等于阵元为N的子阵指向性函数D1(N, d1, λ, θ1)与阵元为M的子阵指向性函数D2(M, d2, λ, θ2)的乘积:
(4)
式中,θ1和θ2为两个方向阵列指向性的偏转角度。
从式(4)可知,当平面矩形扬声器阵列的参数M、N、d1、d2、λ、θ1和θ2一定时,指向性只与子阵和等效阵的偏转角度有关。设子阵N的偏转角为方位角α、设子阵M的偏转角为俯仰角θ ,其他条件相同时,改变参数α和θ就能够改变平面矩形阵列的在三维空间形成的指向性,如图2所示。新的指向性函数为:
(5)
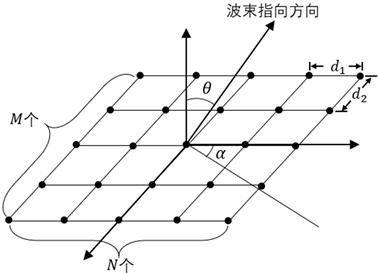
Figure 2. Diagram of planar array directivity deflection
图2. 平面扬声器阵列指向性偏转示意图
3. 扬声器相控阵的仿真
3.1. 线型扬声器相控阵仿真
随着阵元个数n的增多,声波在极坐标中波束宽度越来越窄,这意味着在空间中扬声器阵列的指向性越来越好,即扬声器阵列的指向性与阵元个数n是正相关的,如图3(a)所示。
随着声波频率f逐渐增大,声波波束的宽度越来越小,阵列指向性越来越好,即阵列指向性与声波频率f是正相关的,如图3(b)所示。
随着阵元间距d逐渐增大,声波波束的宽度越小,阵列的指向性越来越好,即阵列指向性与阵元间距d是正相关的。在上述三个仿真图中,除指向90˚的主瓣波束外,在主瓣附近有一些小的波瓣,这些波瓣称为旁瓣,随着主瓣波束的宽度越来越小,由于声波叠加而成的旁瓣数量和旁瓣的大小也会不断增加,这些旁瓣会使得声波辐射变得不均匀,所以,减小旁瓣的数量和旁瓣的大小也是对扬声器阵列进行优化设计的重点,如图3(c)所示。
值得注意的是,根据Nyquist采样定理,为了避免空间混叠现象的发生,在设计仿真和实验时,阵元间距要小于声波的半波长,即需要满足d < λ/2,否则就会在其他方向产生与主瓣大小相等的栅瓣波束 [18]。扬声器阵列产生栅瓣仿真结果如图3(d)所示,这种情况并不是笔者想要的。
通过偏转波阵面实现阵列波束的偏转理论上可以使波束偏转90˚,但由于实际的扬声器并不能够完全视为一个点声源,且在实验中会存在一定的干扰因素,为了便于后续实验测试,仿真实验设计为使波束偏转0˚到20˚,步长为5˚的小角度偏转。图3(e)为f = 1600 Hz,n = 10 ,d = 0.1 m,阵列波束偏转0˚到20˚的仿真图。
只改变波束的偏转角度,对波束主瓣和旁瓣波束的大小和宽度都不会产生影响,波瓣性质与不发生偏转时一致;然而,当波束发生偏转时,偏转侧的旁瓣数量减少,另一侧旁瓣数量增加,偏转角度越大,该现象越明显。
3.2. 平面扬声器相控阵仿真
由式(4)可知,平面矩形阵列的指向性与M、N、d1、d2、α和θ有关,按照线型阵列的仿真思路,将平面阵列阵元数设定为4 × 4,阵列形状设置为正方形,即d1 = d2 = d。此时指向性是α和θ的函数,将其置于直角坐标系中得到三维指向性图。当d = 0.1 m,声源频率f = 1600 Hz时,阵列指向性未发生偏转时不同角度的仿真结果如图4所示。
从图4(a)可以看出,阵列的中心产生了极大指向性波束,即主瓣。主瓣附近有四个较大的旁瓣,旁瓣与声场对称分布。将得到的仿真结果的XOZ面和YOZ面投影到极坐标中得到二维指向性,与线型阵列仿真结果完全一致,即平面扬声器矩阵的指向性函数满足乘积定理。
改变阵列的方位角和俯仰角,以同样的方式得到阵列指向性为(18˚, 45˚)时不同角度的仿真结果如图5所示:
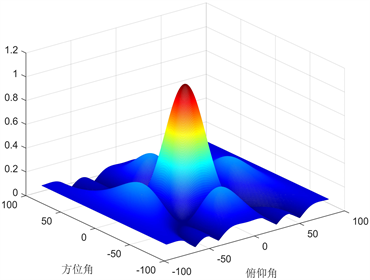
 (a) 直角坐标系中不同角度的仿真结果
(a) 直角坐标系中不同角度的仿真结果 
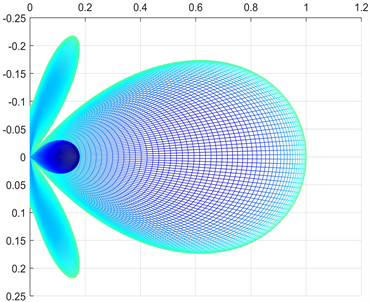 (b) 极坐标系中不同角度的仿真结果
(b) 极坐标系中不同角度的仿真结果
Figure 4. Directivity simulation results when the spatial pointing angle is (0˚, 0˚)
图4. 空间指向角为(0˚, 0˚)时指向性仿真结果

 (a) 直角坐标系中不同角度的仿真结果
(a) 直角坐标系中不同角度的仿真结果 
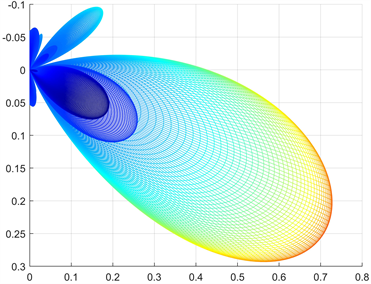 (b) 极坐标系中不同角度的仿真结果
(b) 极坐标系中不同角度的仿真结果
Figure 5. Directivity simulation results when the spatial pointing angle is (18°, 45°)
图5. 空间指向角为(18°,45°)时指向性仿真结果
此时指向性波束已经不在阵列的中心,主瓣偏移到了俯仰角18˚、方位角45˚的位置,此时旁瓣和声场的对称性减弱,但是依旧具有一定的对称性。将结果的XOZ面和YOZ面投影到极坐标中,极坐标偏转角度分别为18˚和45˚,同样满足平面阵列的乘积定理。
由于平面阵列的指向性是线型阵列的叠加,所以在线型阵列产生栅瓣的时候,平面阵列同样会产生栅瓣,即满足d > λ/2 。仍以阵元个数为4 × 4、声源频率f = 1600 Hz的平面阵为例,当d = 0.25 m 时,仿真结果如图6所示:
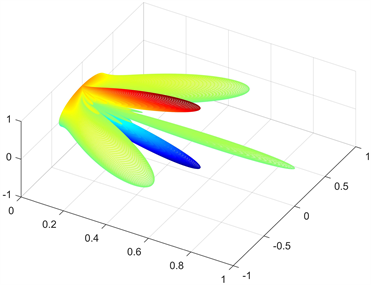
Figure 6. Directivity simulation results of planar array with grating lobes
图6. 具有栅瓣的平面阵列指向性仿真图
由以上仿真结果可得,线型扬声器阵列的性质和条件同样适用于平面扬声器阵列。平面阵列可以视为多个具有相同结构的线型阵列的叠加,指向性上满足乘积定理,在设计阵列时要满足d < λ/2以避免栅瓣的产生。
4. 实验测试与结果分析
4.1. 线型扬声器相控阵测试
实验系统结构如图7(a)所示,稳压电源为功放供电,利用LabVIEW编写程序,NI-9923声卡提供不同频率、幅值为2.2的单频信号,NI-9173和传声器采集设置点的声压,在极坐标内绘制波束指向性曲线并与仿真结果对比。实验阵列选用14个经幅值和初相位校准过的Hivi-S3W-SE 2.0扬声器及其配套功放搭建而成。为增加实验的准确性,实验场地选为可视为半自由场的宽阔露天安静停车场,背景噪声稳定在45到50 dB,实验温度约为25℃,声速约为346 m/s。实验采用10个130E22型传声器,将其设置在与扬声器阵列等高、距阵列中心5 m的圆弧型测点上,每5˚设置一个传声器,每次测量1/4个半圆周,分四次测量全部声场,实验图测试如图7(b)所示:
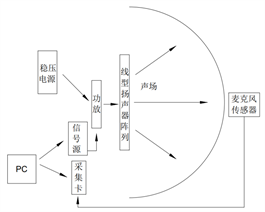 (a) 实验结构图
(a) 实验结构图  (b) 实验测试图
(b) 实验测试图
Figure 7. Diagram of experimental structure and test
图7. 实验结构图和测试图
实验设计与仿真思路相同,采用控制变量法改变f、n、d三个参数,在极坐标内与仿真对比。部分实验结果如图8所示,其中蓝色线条为仿真结果、黑色点划线为实验测试结果:
 (a) f = 500 Hz、n = 10、d = 0.10 m
(a) f = 500 Hz、n = 10、d = 0.10 m 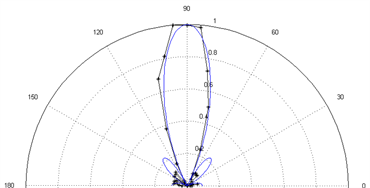 (b) f = 500 Hz、n = 10、d = 0.15 m
(b) f = 500 Hz、n = 10、d = 0.15 m 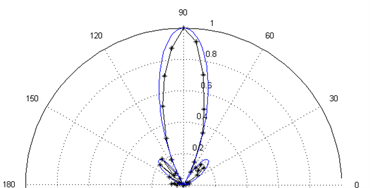 (c) f = 500 Hz、n = 14、d = 0.10 m
(c) f = 500 Hz、n = 14、d = 0.10 m 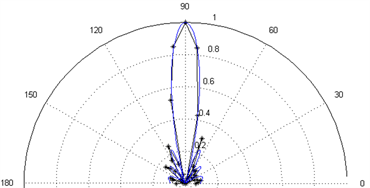 (d) f = 1250 Hz、n = 10、d = 0.10 m
(d) f = 1250 Hz、n = 10、d = 0.10 m
Figure 8. Comparison of simulation and experiment when the array pointing beam is not deflected
图8. 阵列指向波束不偏转时仿真与实验结果图
阵列波束不偏转时,仿真与实验结果重合度极高,大部分的主瓣实验测试点的结果都能够很好的落在仿真结果上,不仅如此,旁瓣的数量和大小也基本可以与仿真结果重合。频率和阵元个数不变时,增大阵元间距能够获得更窄的主瓣,即获得更好的指向性,如图8(a) (b),此时整个阵列的尺寸也会随之增大。当频率和阵元间距固定不变时,增加扬声器的个数能够获得更好的指向性,如图8(a) (c)。当阵元个数和间距都不变时,增加声频率同样可以获得更好的指向性,如图8(a) (d)。

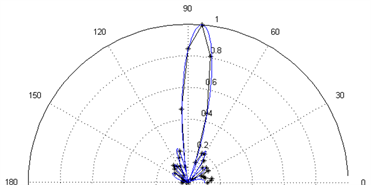
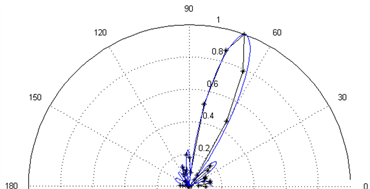
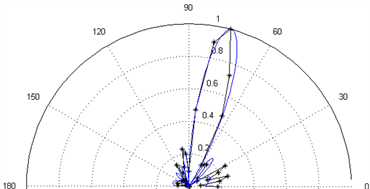
Figure 9. Comparison of simulations and experiments when f = 1250 Hz, n = 10, d = 0.10 m (5˚~20˚)
图9. f = 1250 Hz、n = 10、d = 0.10 m指向性偏转实验图(5˚~20˚)
选取某一工况进行波束偏转实验,如图9所示,实验与仿真结果相同,阵列的指向性偏转并不会使主瓣性质发生变化,大部分主瓣实验测试结果仍然能够完美落在仿真曲线上。当主瓣发生偏转时,旁瓣也会随之偏转,其结果同样与仿真结果一致。一部分测量点没有完全落在仿真图上,其原因主要是由于实验条件等方面的限制,如存在一定的背景噪声、扬声器或传声器无法做到完全一致等。
在仿真结果中,扬声器阵列不产生栅瓣的条件是d < λ/2,在实验中做了几组对比试验来验证产生栅瓣的情况,实验选择f = 1600 Hz,n = 6,d = 0.3 m,结果如图10所示:
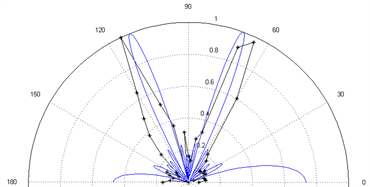
Figure 10. Experimental results of no deflection and 20° deflection with grating lobes when f = 1600 Hz, n = 6, d = 0.30 m
图10. f = 1600 Hz、n = 6、d = 0.30 m不偏转与偏转20°的栅瓣偏转实验图
从图上能直观看出,当d > λ/2时,在仿真中会产生两个极大的栅瓣,在实验中,由于实际声场环境更加复杂,部分实验测量得到的栅瓣与主瓣大小不同,但是实验结果和仿真旁瓣的位置基本一致。在偏转到20˚时,栅瓣与主瓣大小也几乎相同,实验和仿真结果基本重合。验证了理论上当d > λ/2时,扬声器阵列声波会在空间中产生混叠,产生与主瓣大小相同的栅瓣。
4.2. 平面扬声器相控阵测试
由于平面矩形扬声器阵列所产生的声场更加复杂,为降低背景噪声的干扰,使实验结果更准确,平面阵列的实验在一个2.5 m × 2.5 m × 3.2 m 的半消声室进行,背景噪音约为25 dB,扬声器、传声器等设备同线型阵列实验。将扬声器固定在一正方形铁板上,阵列置于吸音棉上,减小地面反射对实验的影响。实验时,每间隔18˚设置传声器,共11个传声器可测量阵列上方180˚范围内,传声器距阵列中心1.8 m。实验时,通过阵列下的转盘使每次阵列转动15˚,实现传声器覆盖阵列上方俯仰角180˚、方位角360˚范围内的空间,如图11所示:

Figure 11. Diagram of experiment and 11 microphones layout
图11. 实验测量及11个传声器布置图
同仿真结果一样,将实验测量到的每个点的声压值依次相连,通过插值拟合为平滑的空间指向性图,并投影到直角坐标系中,与仿真结果进行对比。当阵元个数为4 × 4,阵元间距d = 0.1 m,声波频率f = 1000 Hz,指向角为(18˚, 45˚)的实验结果如图12所示:
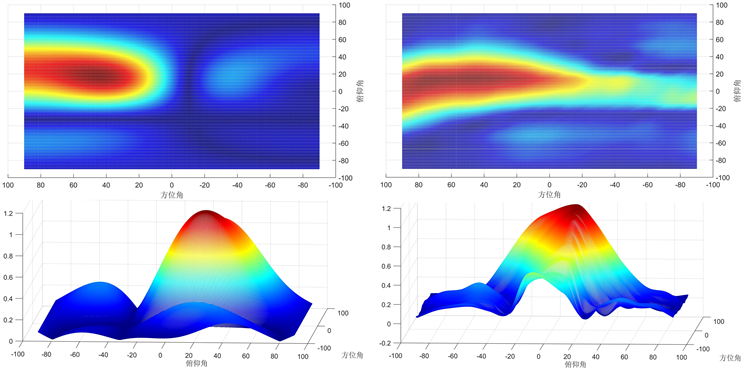 (a) 直角坐标系中不同角度的对比结果(左为仿真结果、右为实验结果,下同)
(a) 直角坐标系中不同角度的对比结果(左为仿真结果、右为实验结果,下同) (b) 极坐标系中不同角度的对比结果
(b) 极坐标系中不同角度的对比结果
Figure 12. Experimental results when the spatial pointing angle is (18˚, 45˚)
图12. 空间指向角为(18˚, 45˚)时实验结果
不论是直角坐标系中还是极坐标系中,实验和仿真一致性都很好。仿真结果中声场区域外的声压值为0,而实验中存在一定的背景噪音,空间上声压不可能为0,所以在图12(a)中仿真结果是闭合曲面,而实验结果为非闭合曲面。在直角坐标系中主瓣区域的分布几乎相同,声场分布也大致相同;在极坐标系当中,主瓣偏移角度和旁瓣大小数量均一致。
上述仿真与实验的对比表明,实验与仿真的结果高度重合,平面阵列的各性质与线型阵列具有一定的相似性。在设计平面扬声器阵列实验时,仿真结果可信,利用相控阵理论可对平面矩形扬声器阵列指向性进行精准控制。
4.3. 实验结果分析
对于线型扬声器阵列来说:
1) 随着阵元个数n、阵元间距d、声源频率f,的增加,主瓣宽度变小,阵列的指向性变好,但是空间中声波的辐射变得不均匀,旁瓣数量和大小会增加,仿真与实验都验证了这一点;
2) 阵列所产生的指向性能够在一定范围内精准控制,指向性的偏转并不会对阵列的性质产生影响;
3) 在设计扬声器阵列时,要满足条件d < λ/2,否则在空间中会产生与主瓣大小相同的栅瓣,随着主瓣偏转,栅瓣也会偏转,在设计阵列时要避免栅瓣的产生。
对于平面矩形扬声器阵列来说:
1) 平面矩形扬声器可以视作多个具有相同结构的线型扬声器阵列平行排列而成,在性质上与线型阵列具有一定的相似性,其指向性满足乘积定理;
2) 不论是主瓣位置与大小,还是旁瓣的数量与大小,平面扬声器阵列实际声场分布与仿真具有高度的一致性,利用相控阵的原理能够对其波束指向进行精确控制。扬声器阵列可以作为空间有向大功率声源使用。
5. 结论
本次工作对线型和平面扬声器相控阵列的三维声场指向性和波束偏转进行了研究。阐述了相控阵的原理、指向性及偏转方法,对不同参数的线型、平面扬声器阵列进行仿真,进行实验测试,验证仿真的准确性,并利用相控阵原理在三维空间中对阵列形成的指向性实现了偏转的精准控制。扬声器相控阵列在低频频率下具有较强指向性,指向性方向精准可控,能量利用率高,可作为有源噪声控制中的大功率控制声源使用。
致谢
感谢导师唐俊副教授对本论文的悉心指导,感谢课题组的同学对本实验的帮助。
基金项目
装备预先研究项目(公开),61402100104,振动与噪声控制新器件应用开发。