1. 引言
实际工程应用的设计工作中,动力学的设计与分析是不可缺少的环节。动力问题是现代工程结构都需要挑战的困难。在航空航天领域,动力学问题尤为突出。轴和轮盘等旋转结构在航空航天领域大量存在并且占据航空航天领域重要的一环。近年来陶瓷基复合材料在航空航天领域的应用越来越广泛,高比强度、耐高温、抗氧化和抗腐蚀是陶瓷基复合材料的特点。由于以上特性,陶瓷基复合材料是用来制造涡轮转子轮盘的理想材料 [1] [2] [3] [4]。陶瓷基复合材料涡轮转子整体轮盘是整体采用陶瓷基复合材料,一体化制造的小型航空发动机涡轮转子整体叶盘。由于陶瓷基复合材料内部细观结构、纤维/基体界面相互作用以及组成材料的属性等细观特征影响陶瓷基复合材料的整体力学和物理性能 [5] [6] [7] [8]。
整体叶盘是航空发动机中主要连接和受力零件,由于目前发动机追求轻重量和长寿命等特性,因此在高负载的工况下,轮盘因振动疲劳而断裂的故障有所增多。一旦发生共振或疲劳,就可能导致严重事故,因此需对轮盘叶片的振动研究更加重视 [9] [10]。黄爱萍 [11] 研究某型发动机压气机轮盘振动特性以及共振转速,采用激光全息干涉法对某型发动机一级压气机盘进行振动试验研究,在0~15,000 Hz频率范围内获得了7个振动模态的静频及振型,并根据实验结果研究该轮盘的行波振动,分析轮盘的共振特性以及临界转速,但只有试验结果分析,缺少对轮盘结构振动特性的仿真分析。由于等学者 [12] 通过建立航空发动机典型轮盘结构三维有限元模型,利用传递矩阵法完成特定振型下的结构模态测试与参数识别,但其研究成果只是在特定振型下较好,未能推广到全部结构模态测试。
本文以陶瓷基复合材料整体叶盘为研究对象。通过仿真软件计算,首先对陶瓷基复合材料整体叶盘的单独叶片计算前4阶固有频率及其对应的振型。其次对去除叶片的陶瓷基复合材料轮盘,计算前4阶固有频率及其对应振型。最后对整体叶盘,仿真计算固有频率,分析叶片对轮盘的影响,以及陶瓷基复合材料整体叶盘的振动特性分析。
2. 模型建立及叶片分析
2.1. 模型建立
仿真模型如图1(a)所示。其中内盘直径60.4 mm,陶瓷基复合材料整体轮盘含叶片的总直径为84.04 mm,其中心开孔的直径为11.0 mm,整体叶盘的厚度为8.0 mm。使用COMSOL Multiphysics结构力学模块进行仿真分析,对模型使用自由四面体网格划分如图1(b)所示,其中网格包括22,089个域单元,12,088个边界元以及2358个边单元。仿真计算使用材料属性为:杨氏模量Ex = Ey = 95 GPa,Ez = 31 GPa,泊松比μ = 0.2,密度2.28 g/cm3。
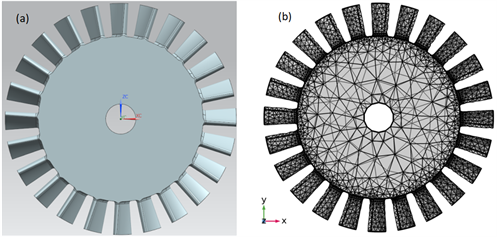
Figure 1. Blade disk model and its meshing
图1. 轮盘模型及其网格划分
2.2. 叶片固有频率计算
为了得到叶片本身的固有频率与振型模态,将单个叶片区域拿出作为研究对象,单个叶片如图2(a)所示,将叶片置于固定端,即如图2(b)所示的固定边界,通过COMSOL计算得到整体叶盘的单个叶片前四阶固有频率以及对应主振型为:14,006.0 Hz、34,600.0 Hz、42,109.0 Hz以及73,865.0 Hz对应模态振型如图3所示。
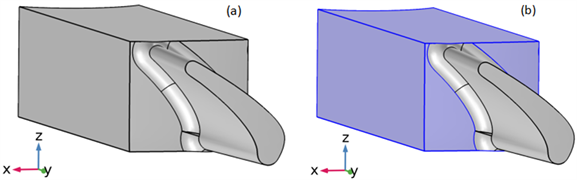
Figure 2. Single blade model and fixed constraint end schematic diagram
图2. 单个叶片模型及固定约束端示意图
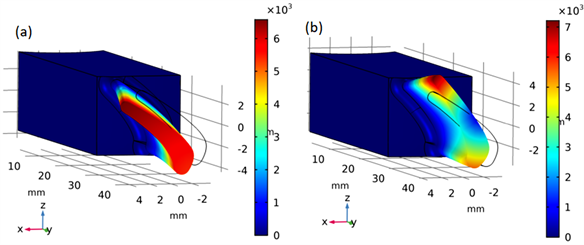
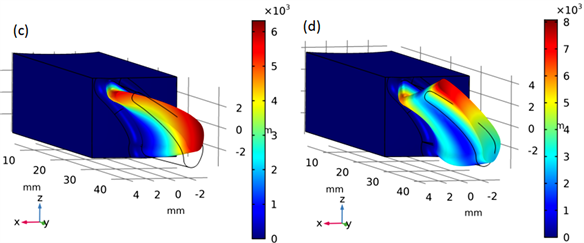
Figure 3. The first four order main modes of a single blade: (a) First order natural frequency 14,006.0 Hz; (b) Second order natural frequency 34,600.0 Hz; (c) Third order natural frequency 42,109.0 Hz; (d) Fourth order natural frequency: 73,865 Hz
图3. 单个叶片前4阶主振型:(a) 一阶固有频率14,006.0 Hz;(b) 二阶固有频率34,600.0 Hz;(c) 三阶固有频率42,109.0 Hz;(d) 四阶固有频率73,865.0 Hz
3. 轮盘自由状态固有频率分析
接下来,针对未安装叶片时中间的单独轮盘,分析陶瓷基复合材料轮盘自由约束下的振型模态如图4所示,其中轮盘的固有频率分别为:12,527.0 Hz、19,439.0 Hz、28,548.0 Hz、40,661.0 Hz。单独轮盘为对称结构,其陶瓷基复合材料轮盘振型明显呈对称形态。
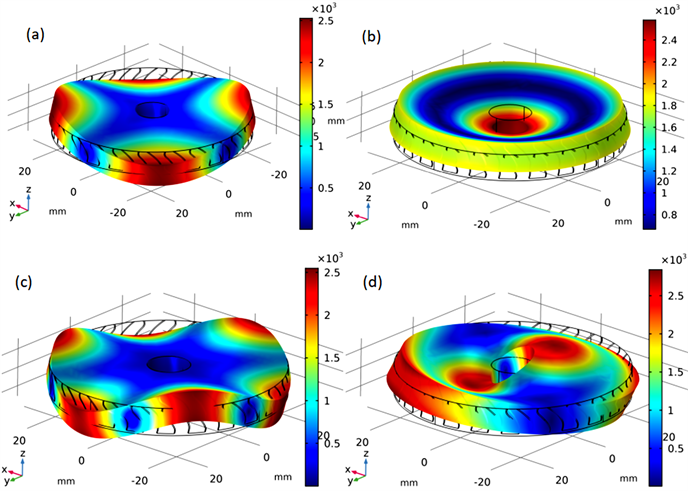
Figure 4. The first four main modes of a single wheel: (a) First order natural frequency12,527 Hz; (b) Second order natural frequency 19,439 Hz; (c) Third order natural frequency 28,548.0 Hz; (d) Fourth order natural frequency 40,661.0 Hz
图4. 单个轮盘前4阶主振型:(a) 一阶固有频率12,527.0 Hz; (b) 二阶固有频率19,439.0 Hz;(c) 三阶固有频率28,548.0 Hz;(d) 四阶固有频率40,661.0 Hz
4. 整体叶盘模态固有频率分析
然而,由于实际安装时轮盘和叶片为一整体结构,则应该考虑轮盘和叶片同时处于全自由约束时的固有频率,则添加自由条件如图5所示,轮盘及叶片外部均为自由端。
Figure 5. Global leaf disk free constraints
图5. 整体叶盘自由约束条件
仿真得到如图6的模态振型,可以看出由于中心盘和外围叶片的耦合,出现了相当多的耦合模态,图6(a)~(h)分别对应自由约束固有频率为:8712.9 Hz、12,093.0 Hz、12,721.0 Hz、13,219.0 Hz、18,364.0 Hz、20,277.0 Hz、26,220.0 Hz、29,356.0 Hz。

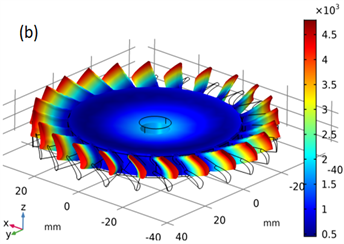
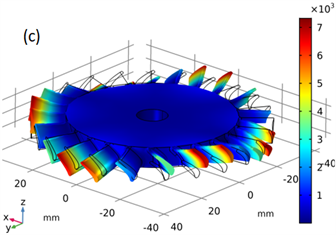
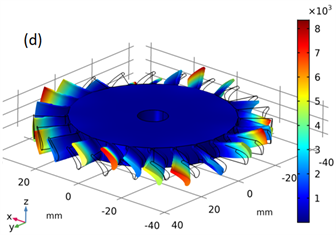
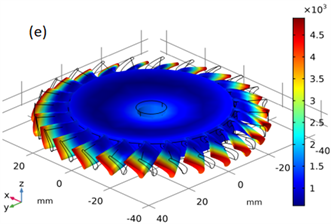
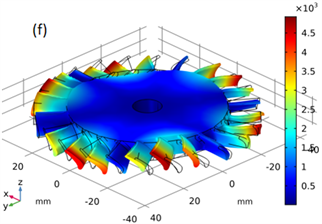
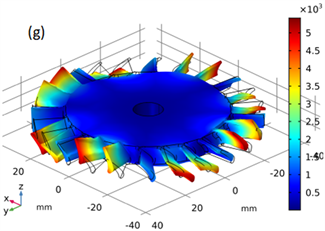
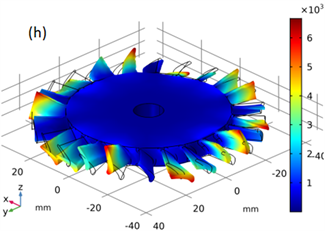
Figure 6. Shape model of blade-disk: (a) First-order natural frequency of the whole leaf disk 8712.9 Hz; (b) Second-order natural frequency of the whole leaf disk 12,093.0 Hz; (c) Third-order natural frequency of the whole leaf disk 12,721.0 Hz; (d) Fourth -order natural frequency of the whole leaf disk 13,219.0 Hz; (e) Fifth-order natural frequency of the whole leaf disk 18,364.0 Hz; (f) Sixth -order natural frequency of the whole leaf disk 20,277.0 Hz; (g) Seventh-order natural frequency of the whole leaf disk 26,220.0 Hz; (h) Eighth -order natural frequency of the whole leaf disk 29,356.0 Hz
图6. 整体叶盘振型模态:(a) 整体叶盘一阶固有频率为8712.9 Hz;(b) 整体叶盘二阶固有频率为12,093.0 Hz;(c) 整体叶盘三阶固有频率为12721.0 Hz;(d) 整体叶盘四阶固有频率为13219.0 Hz;(e) 整体叶盘五阶固有频率为18,364.0 Hz;(f) 整体叶盘六阶固有频率为20,277.0 Hz;(g) 整体叶盘七阶固有频率为26,220.0 Hz;(h) 整体叶盘八阶固有频率为29,356.0 Hz
其中较为明显的为:
图6(a)为中间盘一阶模态与外缘部分叶片不同相位的一阶模态的耦合结果;
图6(b)与图6(e)的中间盘二阶模态与外缘全部叶片相位一致的一阶耦合振型,其中图6(b)的中间盘与叶片相位相同,图6(e)的中间盘与叶片相位相反;
图6(c)和图6(f)为中间盘三阶模态与外缘部分叶片不同相位的一阶模态的耦合结果;
图6(d)为外缘叶片之间不同模态、相位等组合构成的耦合模态,另实际在13,000 Hz附近有较多不同组合模式的耦合模态,在这里省略不做额外分析;
图6(g)和图6(h)为中间盘的更高阶模态与叶片及叶片前三阶模态的不同组合得到的耦合模态。
综上可知:叶片对轮盘的固有频率影响很大,在整体叶盘的仿真分析中,带有叶片的轮盘振动,实际是轮盘和叶片的耦合振动,其整体叶盘的振动和单个轮盘的振动特性不同。图4与图6对比中,图4中的单个轮盘振动特性明显呈对称,且都是弯曲振动。图6中的整体叶盘的振动,由于受到叶片弯扭振动的耦合影响,使得整体叶盘的前8阶振型有几个不是对称振型,叶片与轮盘的耦合振动,使得叶盘形成的几个振型与轮盘本身的振型相同,但固有频率不一样的振型。
5. 结论
对陶瓷基复合材料整体叶盘的振动特性,采用仿真计算得出单个叶片与轮盘的前4阶固有频率及其振型。再对整体叶盘仿真计算前8阶固有频率及其振型。得出:陶瓷基复合材料整体叶盘的振动特性与单个轮盘的振动特性明显不同。叶片与轮盘的耦合振动,使得整体叶盘形成的几个振型与轮盘本身的振型相同,但固有频率不一样的模态。从而为陶瓷基复合材料整体叶盘的动态响应提供参考数据,与此同时能为陶瓷基复合材料整体叶盘结构的振动特性优化设计提供依据。
NOTES
*通讯作者。