倾斜长周期光栅级联谱特性及折射率传感研究

Cascade Spectrum Characteristics and Refractive Index Sensor of Long Period Tilted Grating

摘要: 基于耦合模式理论和折射率传感理论，通过传输矩阵法分析了级联倾斜长周期光纤光栅(Cascade Tilted Long Period Fiber Bragg, CTLPFG)的光谱特性和折射率传感特性。本文分别模拟了不同级联长度、级联角度、级联位置下的CTLPFG的谱特性，最后又模拟了不同环境折射率对CTLPFG不同包层模式的有效折射率的影响。研究结果表明：级联长度达到一个周期长度或者级联位置靠近光栅两端时，传输谱中的两个主损耗峰会逐渐变成一个主损耗峰；当只改变一个TLPFG倾角时，会对损耗峰的带宽产生影响；包层模式的有效折射率会随着外界环境折射率的增大而增大，并且高阶包层模式的有效折射率对环境折射率的变化更加敏感。因此，可以通过利用CTLPFG的不同参量之间的互补特性来设计出所需要的传输谱。

Abstract: Based on coupling mode theory and refractive index sensing theory, The spectral characteristics and refractive index sensing characteristics of cascaded inclined long-period fiber grating (Cascade Tilted Long Period Fiber Bragg, CTLPFG) were analyzed by transmission matrix method. In this paper, the spectral characteristics of CTLPFG with different cascade lengths, cascade angles and cascade positions are simulated respectively. Finally, the effects of different ambient refractive index on the effective refractive index of CTLPFG with different clad-ding modes are simulated. he results show that when the cascade length reaches a period length or the cascade position is close to the two ends of the grating, the two main loss peaks in the transmis-sion spectrum gradually become one main loss peak. When only one TLPFG Angle is changed, the bandwidth of the loss peak will be affected. The effective refractive index of cladding mode increas-es with the increase of ambient refractive index, and the effective refractive index of higher order cladding mode is more sensitive to the change of ambient refractive index. Therefore, the required transmission spectrum can be designed by using the complementary characteristics between dif-ferent parameters of CTLPFG.

1. 引言

倾斜长周期光纤光栅(TLPFG)作为一种新型的光栅传感器，相对于以往普通的长周期光纤光栅(LPFG)有很多的优势，例如对环境折射率的灵敏度更高，重量更轻，交叉灵敏度更低等。倾斜长周期光纤光栅已经在很多领域发展开来，这其中包括脑部和机体弯曲的传感器、化学折射率传感器 [1] 。倾斜长周期光纤光栅的周期范围在几十微米到几百微米之间，当同向传输的纤芯模和包层模满足相位匹配的条件时发生耦合，从而在其光谱图中会出现很多不同的损耗峰 [2] ；在倾斜长周期光纤光栅中，纤芯模和一阶包层模的耦合被增强，光栅倾斜角度的存在造成光能量从纤芯模耦合到包层模当中。高阶包层模的耦合对于单独的光纤光栅能够用于增加可用的传感模式，而且利用来自倾斜长周期光栅的大量可用数据也能够增加传感器的灵敏度 [3] [4] 。

相对于单独的长周期光纤光栅，多根级联后的光纤光栅光谱的设计更具有灵活性，也更容易发现新的特性。1998年，Ke等 [5] 在理论上分析了相移后的长周期光纤光栅的谱特性，并通过理论模拟了不同相移的长周期光纤光栅光谱特性；2011年，樊彦恩 [6] 结合级联光栅和相移长周期光纤光栅理论，研制出一种基于旋转折变型长周期光纤光栅的马赫曾德干涉仪(RLPFG-MZI)，这种干涉仪是由两个旋转折型的长周期光纤光栅(RPLFG)级联而制成，并在理论上分析研究了这种折射仪的折射率传感原理和光学特性。研究表明，这种干涉仪在环境折射率为1.33~1.36区间内的线性响应度比较好，当其光栅旋转角度达到130˚时，它的折射率灵敏度为14.7 pm/mm；2018年，高敏 [7] 等人利用传输矩阵法研究了两个不同参数的长周期光纤光栅级联后的传输谱，结果表明：级联长度不同的光栅和光纤，以及有效折射率的调制对传输光谱均有影响，通过改变级联长周期光纤光栅的参数可以实现不同特性的传输谱。

本文基于光纤光栅耦合模式理论和折射率传感理论，利用传输矩阵法分析了倾斜长周期光纤光栅级联的传输特性和环境折射率传感特性。通过改变倾斜角度、级联长度、级联位置和环境折射率等参数仿真分析了倾斜长周期光纤光栅级联的传感特性。

2. 理论分析

2.1. 倾斜长周期光纤光栅的结构

倾斜长周期光纤光栅结构如图1所示， $\theta$ 表示TLPFG的栅格波矢方向与光纤切面方向的夹角，纤芯的折射率为n₁，纤芯半径为r₁，包层的折射率为n₂，包层半径为r₂，环境折射率为n₃，光栅的轴向周期为Λ，倾斜栅格间的距离为Λ_g，且满足 ${\Lambda }_g=\Lambda \cos \theta$ ，级联倾斜长周期光纤光栅如图2所示，其中d为级联长度。

Figure 1. Schematic diagram of TLPFG

图1. TLPFG示意图

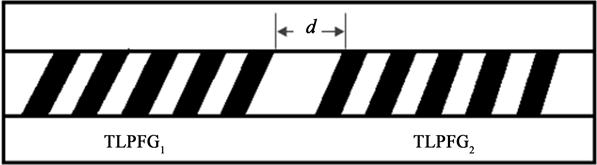
Figure 2. Schematic diagram of CTLPFG

图2. CTLPFG示意图

2.2. 耦合模式理论

通过查阅文献 [8] [9] [10] 了解到，倾斜长周期光纤光栅的耦合模式方程为

$\frac{\text{d}{A}_{co}}{\text{d}z}=i{f}_{co-co}+i{\displaystyle {\sum }_{l,m}{g}_{lm-co}^{+}{A}_{lm}}\times \exp \left(-2i{\delta }_{lm-co}z\right)$ (1)

${\displaystyle {\sum }_{l,m}\left[\frac{\text{d}{A}_{lm}}{\text{d}z}=i{A}_{lm}{f}_{lm-lm}+i{g}_{01-lm}^{-}{A}_{01}\times \exp \left(2i{\delta }_{01-lm}z\right)\right]}$ (2)

式子中 $A_{co}$ 是纤芯模的振幅，i为虚数单位， $f_{co-co}$ 、 $g_{lm-co}^{+}$ 和 $f_{lm-lm}$ 分别是纤芯模与纤芯模之间、纤芯模与包层模之间和包层模与包层模之间的耦合系数， $A_{lm}$ 是l阶m次的包层模振幅， ${\delta }_{lm-co}$ 是l阶m次包层模与纤芯模的解调参量。由于折射率调制主要与纤芯模自耦合和纤芯模与包层模之间的耦合有关，包层模与包层模之间的耦合可以忽略不计，因此耦合系数计算公式 [11] [12] [13] 如下：

$f_{co-co}=\frac{\omega }{2}{\epsilon }_0{n}_1^2\delta \left(z\right){\displaystyle {\int }_0^{2\pi }\text{d}\phi }{\displaystyle {\int }_0^{a_1}r\text{d}r}\left(E_r^{co}{E}_r^{c{o}^{\text{*}}}+E_{\phi }^{co}{E}_{\phi }^{c{o}^{\text{*}}}\right)$ (3)

$g_{lm-co}^{\pm }=\frac{\omega }{4}{\epsilon }_0{n}_1^2\delta \left(z\right)v{\displaystyle {\int }_0^{2\pi }\text{d}\phi }{\displaystyle {\int }_0^{a}r\text{d}r}\exp \left(\mp 2i{K}_{g}r\cos \phi \sin \theta \right)\left(E_r^{cl}{E}_r^{c{o}^{\text{*}}}+E_{\phi }^{cl}{E}_{\phi }^{c{o}^{\text{*}}}\right)$ (4)

${\delta }_{cl-co}=\frac{1}{2}\left({\beta }_{co}-{\beta }_{lm}-2K_g\cos \theta \right)$ (5)

上述公式中， $\theta$ 、r、 $\phi$ 都是球坐标系中的坐标参数， $\omega$ 是光波角频率， $E_r$ 和 $E_{\phi }$ 分别是模式场的径向分量和切向分量， ${\epsilon }_0$ 是真空中的介电常数， $\delta \left(z\right)$ 是在z方向上纤芯折射率的变化量， $a_1$ 是纤芯的半径大小，

v是条纹可见度， $K_g=\frac{\pi }{{\Lambda }_g}$ ， ${\beta }_{co}$ 是纤芯模的传播常数， ${\beta }_{lm}$ 是l阶m次包层模的传播常数。当解调参量

${\delta }_{lm-co}=0$ 时，即倾斜长周期光纤光栅满足相位匹配条件时，可以推出： $\lambda =\left[n_{eff}^{co}\left(\lambda \right)-n_{eff}^{lm}\left(\lambda \right)\right]\Lambda$ ，式中， $n_{eff}^{co}$ 为纤芯的有效折射率， $n_{eff}^{lm}$ 是包层的有效折射率，可以通过求解圆柱型多层光纤光栅的特征方程来求得有效折射率。从上述式子中可以看出， $\theta$ 的改变会影响 $g_{lm-co}^{\pm }$ ，进而影响谱透射率的大小。

2.3. CTLPFG的传输理论分析

当入射光进入TLPFG₁时，由于光栅倾斜角的存在，使得其中一部分光波能量会被耦合进包层中，这部分光波能量会在包层中发生损耗，但级联长度d有限，所以损耗的光波能量也有限。当光波传输到TLPFG₂时，包层中的光波能量又被重新耦合进纤芯中，与原来在纤芯中传输的光波能量发生耦合，展现出与未级联的TLPFG不同的光谱特性 [14] [15] 。

本文采用传输矩阵法来对CTLPFG进行分析计算。在CTLPFG中有两种传输方向的模式，前向传输的纤芯模和后向传输的包层模，并且它们之间可以相互发生耦合。我们可以用2 × 2的矩阵来表示级联处的传输矩阵，然后将每一个传输矩阵顺次相乘得到总的传输矩阵。初始化：设置纤芯模的初始端振幅为 $a_0$ ，包层模的初始端振幅 $b_0$ ，则：

$\left[\begin{array}{c}a\\ b\end{array}\right]=F_M\times F_M^c\cdots F_i\times F_i^c\cdots F_1\times \left[\begin{array}{c}{a}_0\\ b_0\end{array}\right]$ (6)

其中，a是级联后纤芯模的振幅，b是级联后包层模的振幅，M为总的级联段数，光栅位置用第i段表示， $F_i$ 用来代表第i段的传输矩阵， $F_i^c$ 用来代表第i段处的级联传输矩阵，则 $F_i$ 和 $F_i^c$ 为：

$F_i=\left[\begin{array}{cc}{a}_{\text{i}}& b_i\\ b_{\text{i}}& a_{\text{i}}\end{array}\right]$ (7)

$F_i^c=\left[\begin{array}{cc}\exp \left[i\pi \left(n_{eff}^{co}-n_{eff}^{cl}\right)d_g^i/\lambda \cos \theta \right]& 0\\ 0& \exp \left[-i\pi \left(n_{eff}^{co}-n_{eff}^{cl}\right)d_g^i/\lambda \cos \theta \right]\end{array}\right]$ (8)

其中： $n_{eff}^{co}$ 和 $n_{eff}^{cl}$ 分别是纤芯折射率和包层折射率， $d_g^i$ 为第i段光栅与第i + 1段光栅的间距， $\lambda$ 为布拉格波长。此外， $a_i$ 和 $b_i$ 的表达式为：

$a_i=\cos \left(\sqrt{{\hat{\sigma }}^2+k^{2}L}\right)+i\frac{\hat{\sigma }}{\sqrt{{\hat{\sigma }}^2+k^{2}L}}\sin \left(\sqrt{{\hat{\sigma }}^2+k^{2}L}\right)$ (9)

$b_i=i\frac{k}{\sqrt{{\hat{\sigma }}^2+k^2}}\sin \left(\sqrt{{\hat{\sigma }}^2+k^{2}L}\right)$ (10)

其中： $\hat{\sigma }=\frac{\delta +\left({\sigma }_{11}+{\sigma }_{22}\right)}{2}$ ， $\hat{\sigma }$ 为直流耦合系数，k为交流耦合系数， ${\sigma }_{11}$ 为纤芯模的自耦合系数， ${\sigma }_{22}$ 为

包层模与纤芯模的互耦合系数， $\delta$ 为纤芯模与包层模之间的解调系数。初始条件为： $a_0=1$ ， $b_0=0$ ，光

栅的长度为L，级联后的TLPFG的透射率为： $T={\left|\frac{a}{a_0}\right|}^2=a^2$ 。

3. 仿真与结果分析

本文基于TLPFG的耦合模式理论，对TLPFG的光谱进行仿真。除特殊说明外，以下仿真的设置参数为：纤芯半径(r₁)为2.75 μm，纤芯折射率(n₁)为1.4625，包层半径(r₂)为63.5 μm，包层折射率(n₂)为1.4615，环境折射率(n₃)为1，为了方便起见，环境介质半径(r₃)设置为200 μm，折射率调制深度为0.0004，周期为480 μm，光栅倾角( $\theta$ )为60˚，级联的两根TLPFG的长度分别为L₁ = L₂ = 13.5 mm，那么总的光栅长度为L = L₁ + L₂ = 27 mm，级联长度为d，级联的位置参量用Q表示，定义Q = L₁/L − 0.5。

3.1. 级联长度对CTLPFG的传输谱的影响

如图3所示，下列图像为不同级联长度下的级联倾斜长周期光纤光栅的传输谱，选取的级联长度d分别为120 μm、240 μm、360 μm和480 μm。

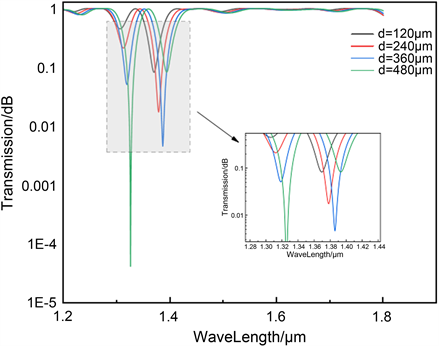
Figure 3. Transmission spectra of CTLPFG at different joint lengths

图3. 不同级联长度下的CTLPFG的传输谱

由图3中CTLPFG传输谱我们可以看到，在1.90 μm附近有两个主损耗峰，随着级联长度的增加，左侧损耗峰深度逐渐增大，右边损耗峰深度逐渐减小，并且整体损耗峰位置逐渐向右移动，波形的带宽基本不变。这表明：在一定的级联长度范围内，随着级联长度的增加，长波处的光耦合量增加，短波处的光耦合量减少。

3.2. 不同倾角对CTLPFG的传输谱的影响

3.2.1. 同时改变两个光栅的倾斜角度

如图4所示，设定光栅的级联长度为240 μm，两光栅的倾斜角度均为60˚、61˚、62˚、63˚，选取CTLPFG的包层模式传输谱图为研究对象。

从图4中我们可以看出，在不同倾斜角度下，CTLPFG的包层模传输谱中出现了两个主损耗峰。随着倾斜角度的增大，左侧损耗峰的深度逐渐减小，右侧损耗峰的深度逐渐增大，并且整体双峰逐渐向长波方向移动，说明倾角的增大使得光栅对长波处的光耦合量增加，对短波处的光耦合量减小。相对于普通的级联长周期光纤光栅而言，倾斜角度的变化对CTLPFG的影响更大，传输谱中的损耗峰值和位置变化更为明显。

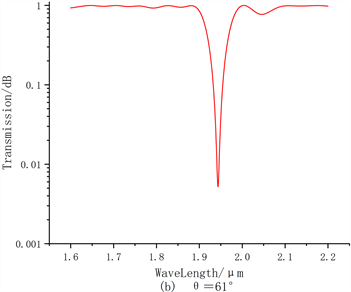
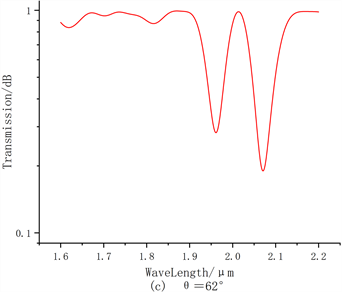
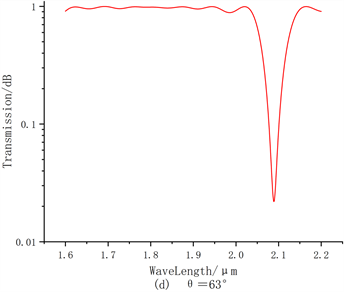
Figure 4. Transmission spectra of CTLPFG at different tilt agles

图4. 不同倾斜角度下的CTLPFG传输谱

3.2.2. 只改变一个光栅的倾斜角度

如图5所示，设定光栅的级联长度为240 μm，固定TLPFG₁的角度( ${\theta }_1$ )为60˚，改变TLPFG₂的角度( ${\theta }_2$ )分别为60˚、61˚、62˚、63˚，选取CTLPFG包层模式的传输谱为研究对象。

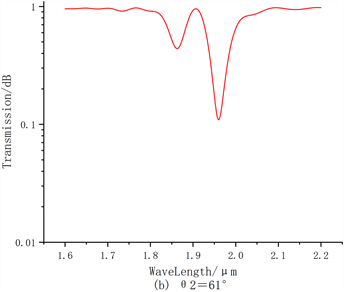
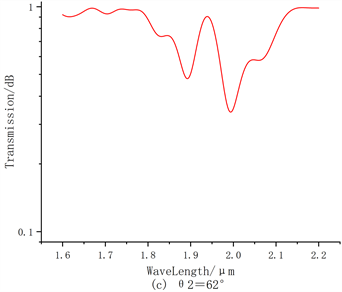
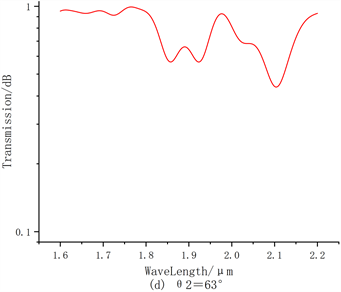
Figure 5. Cascade transmission spectrum for changing the tilt angle of TLPFG₂

图5. 改变TLPFG₂的倾斜角时的级联传输谱

通过上图5我们可以看出，在固定一个TLPFG的倾斜角度，而改变另一个TLPFG的倾斜角度时，传输谱中同样出现了两个主损耗峰。特别的是，在 ${\theta }_2$ 为62˚和63˚传输谱中，两个主损耗峰带宽变大，并且损耗峰的形状也逐渐变成“牙齿状”，透射峰的深度也逐渐变小。所以，通过增大其中一个TLPFG的倾斜角度，可以增加光栅包层模中更多波段光耦合到外界环境中。

3.3. 不同级联位置对CTLPFG的传输谱的影响

如图6所示，设定CTLPFG的级联长度为240 μm，级联位置参数Q设为0、+0.25、−0.25、0.5，其他参数保持不变。

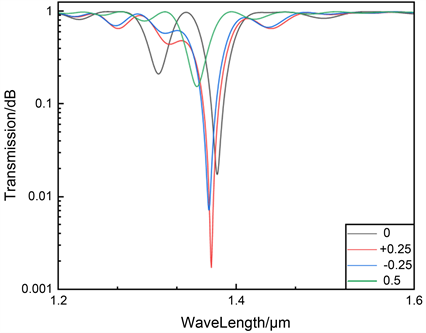
Figure 6. Transmission spectra of CTLPFG with changing cascade position parameters

图6. 改变级联位置参数时的CTLPFG的透射光谱

从图6中我们可以看出，当Q = 0.5时，就类似于单独的一根TLPFG光纤光栅，其透射光谱中只有一个主损耗峰，位置在波长1.90 μm左右。当Q = 0时，在波长1.90 μm附近有两个深度不同的损耗峰；当Q = ±0.25时，两者的透射光谱中的损耗峰的形状类似，位置都在1.80~2.0 μm附近，相对于Q = 0时的两个主损耗峰逐渐融合为一个主损耗峰，并且在主损耗峰周围出现了两个大小类似的旁瓣损耗峰。此外我们可以看出，随着级联位置由中心逐渐向两侧移动时，两损耗峰融合为一个主损耗峰的同时，损耗峰的深度也逐渐变大，当Q = 0.5时的损耗峰深度最大。

3.4. 不同环境折射率对CTLPFG不同包层模式有效折射率的影响

如图7所示，保持其他参数不变的情况下，分别研究了不同环境折射率对CTLPFG的LP_(0,4)、LP_(0,5)以及LP_(0,6)包层模式有效折射率(Effective Refractive Index)的影响。

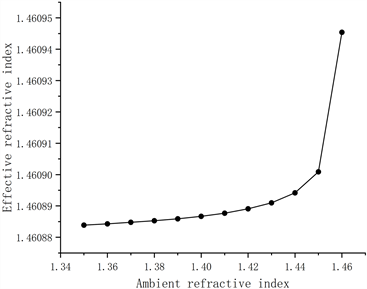
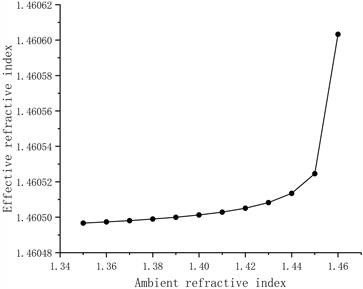LP_(0,4) LP_(0,5)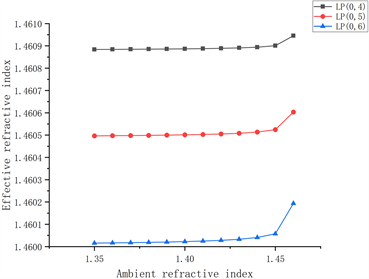LP_(0,6) LP_(0,4)、LP_(0,5)、LP_(0,6)对比图

Figure 7. The relationship between the effective refractive index of different cladding modes and the ambient refractive index

图7. 不同包层模式的有效折射率与环境折射率的关系图

由上图可以看出，三种不同包层模式的有效折射率都随着环境折射率的增大而增大，并且在环境折射率为1.35~1.44 RIU范围内，这三种包层模式的有效折射率增大的效果相对不明显，而在环境折射率为1.44~1.46 RIU范围内，包层模式的有效折射率增大的效果非常明显。从对比图我们可以看出，当环境折射率从1.45 RIU变化到1.46 RIU时，LP_(0,6)包层模式的有效折射率变化量最大，通过计算得出，同一环境折射率范围内，LP_(0,4)包层模式的有效折射率变化量为0.00004446，LP_(0,5)包层模式的有效折射率变化量为0.00007848，LP_(0,6)包层模式的有效折射率变化量为0.00013643，说明高阶包层模式对环境折射率的灵敏度更高，CTLPFG光纤光栅中的高阶包层模式更容易被耦合到外界环境当中。因此，在实际应用当中，我们应该合理选择CTLPFG的包层模式来研究，从而获得所需要的折射率灵敏度。

4. 结论

本文对倾斜长周期光纤光栅级联(CTLPFG)谱特性及折射率传感特性进行了研究，设置所需要的参数，仿真了不同级联长度、倾斜角度以及级联位置对CTLPFG的透射光谱的影响，最后又仿真了环境折射率对不同包层模式的有效折射率的影响。研究发现：不同级联长度和倾斜角度下，CTLPFG的光谱中会出现不同深度大小的损耗峰；当只改变其中一个TLPFG的倾斜角度时，透射光谱中的损耗峰位置和深度大小也会改变，同时主损耗峰的带宽也随之增加；当级联位置逐渐靠近CTLPFG两端时，光谱中的双峰会逐渐融合成一个主损耗峰；最后研究发现CTLPFG高阶包层模式的有效折射率对环境折射率更为敏感。因此，与普通CLPFG相比，CTLPFG可以提供更多的新特性，利用不同参量的相互补偿设计出更加优良的光纤光栅传感器。