1. 引言
股票市场投资是高风险投资,股票的价格和波动率是股票市场中的主要统计指标,对其进行研究可以分析股票市场的风险度量,有助于投资者认识股市风险,进而有助于投资者做出正确的投资决策。股票的价格是随着风险的变化而不断变化的。仅依靠传统直接比率分析的方法在分析风险时就缺乏一定的科学性[1] 。波动率是解释股票风险一个重要因素,为了规避风险,了解风险特征,使投资者获取更大收益,对股票波动率准确估计与预测对风险控制具有极其深远的意义。但由于股票价格等金融时间序列数据往往是不平稳的,样本分布尖峰厚尾,异常值过多等特点,不满足Gauss-Markov条件,因此无论是利用极大似然估计或最小二乘估计处理模型稳健性都会很差,结果误差也很大。
分位数回归本身稳健性的特点决定了在处理样本尖峰后尾,异常值过多的情形能发挥更大的优势。目前已有大量文献利用分位数回归方法研究经济时间序列波动率的问题[2] [3] 。而复合分位数回归[4] 则是分位数回归方法的一种更一般的推广形式,是一种更一般化的估计方法,它依据因变量的多个条件分位数对自变量进行回归,能够精确描述自变量对于因变量的条件变化以及条件分布形状的影响,而且不需要对误差项的分布做出任何具体假定。最近关于复合分位数回归的研究已有大量的文献。比如文献[5] 对非参数回归模型提出了一个局部复合分位数回归统计推断方法。文献[6] 对非线性回归模型则提出了一个加权的复合分位数回归统计推断方法。但是利用复合分位数回归方法研究经济时间序列波动率的问题目前还没有相关文献进行讨论。
基于此,本文引进复合分位数回归技术估计股票波动率。此外在处理过程中,本文对GARCH模型的方差方程进行对数变换,这样不仅保证了模型误差的独立同分布性,而且取对数逆变换后也能保证波动率的非负性。实证分析表明,利用复合分位数回归的方法估计变换后的模型,异常值的敏感程度更低,估计效果更好。
2. 研究方法与模型建立
2.1. 复合分位数回归基本原理
复合分位数回归最初是由Zou和Yuan[4] 提出的一种估计方法,其可以利用因变量的多个条件分位数对自变量做回归,得到其最小估计值。相比较极大似然或最小二乘估计,复合分位数回归不需要对模型误差的分布做出假定,应用条件更为宽松,挖掘的统计信息也更为丰富。
复合分位数回归可如下描述:考虑一组随机样本为 ,
,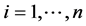 ,其中
,其中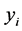 为响应变量,
为响应变量, 为对应用解释变量,并且假定满足如下线性关系:
为对应用解释变量,并且假定满足如下线性关系:
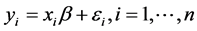
其中 为模型误差,并且有
为模型误差,并且有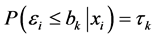 ,
, 。对任意的
。对任意的 ,定义检验函数为
,定义检验函数为 ,
,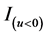 为示性函数。则参数
为示性函数。则参数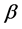 的复合分位数回归估计为
的复合分位数回归估计为
 (1)
(1)
对模型(1)可以采用单纯形法求解,但对于大规模问题其收敛速度还是相对较慢。文献[7] 提出了一种Majorize-Minimize(MM)算法适应大规模问题求解。因此,本文基于MM算法对(1)式求最优解。
2.2. 模型建立
设 表示某种股票第
表示某种股票第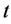 个投资期的收盘价,相应的对数收益为
个投资期的收盘价,相应的对数收益为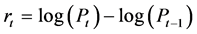 。
。
考虑一般化模型
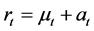 (2)
(2)
其中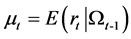 为形如
为形如 等一般的未知非参数函数,
等一般的未知非参数函数, 表示
表示 之前的已有信息,
之前的已有信息,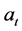 表示随机扰动,并且有
表示随机扰动,并且有
 (3)
(3)
其中 为高斯白噪声过程,则波动率为
为高斯白噪声过程,则波动率为 。取
。取 ,如果
,如果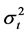 存在ARCH效应,可用多元GARCH(p, q)模型
存在ARCH效应,可用多元GARCH(p, q)模型 表示。为简化此问题,考虑如下可加参数模型:
表示。为简化此问题,考虑如下可加参数模型:
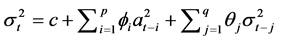 ,
,
记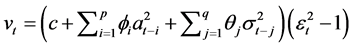 ,那么则有
,那么则有
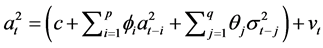 (4)
(4)
注意到 分布是非对称的且存在异方差。为了保证误差项满足独立同分布,对(3)式两边平方取对数可得:
分布是非对称的且存在异方差。为了保证误差项满足独立同分布,对(3)式两边平方取对数可得:
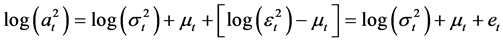 (5)
(5)
这里 ,
, 。由于
。由于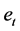 仍然是非对称的,利用极大似然估计估计结果不能保证其有效性。利用复合分位数回归的估计方法不需要对误差分布做假定,对异常值敏感度更低,结果更为稳健,因此接下来考虑利用复合分位数回归方法求解(5)式。类似的,对
仍然是非对称的,利用极大似然估计估计结果不能保证其有效性。利用复合分位数回归的估计方法不需要对误差分布做假定,对异常值敏感度更低,结果更为稳健,因此接下来考虑利用复合分位数回归方法求解(5)式。类似的,对 定义
定义
 ,
,
进行对数逆变换得到
 (6)
(6)
由(6)式可以看出对方差方程做对数变换还可保证波动率的非负性。将(6)带入(5)式即得到如下对数形式的GARCH模型:
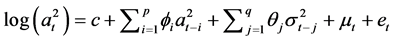 (7)
(7)
2.3. 模型估计算法
对波动率的求解,我们采用复合分位数回归的方法,对(7)式进行复合分位数回归,并且采用迭代向后拟合算法[8] 处理模型中的可加部分。具体方法如下:
第一步:用极大似然方法对波动率做参数GARCH估计,进而得到波动率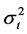 的初估计,记为
的初估计,记为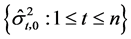 。
。
第二步:取迭代次数 ,做
,做 关于
关于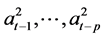 和
和 的向后拟合回归,这里取
的向后拟合回归,这里取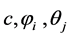 的初估计
的初估计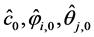 为0,
为0,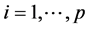 ,
,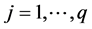 。运用复合分位数回归方法计算
。运用复合分位数回归方法计算 的估计值。
的估计值。
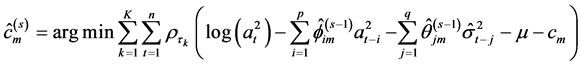 (8)
(8)
 (9)
(9)
 (10)
(10)
反复对(8)~(10)式迭代计算直到足够的精度,即得到 的向后拟合估计:
的向后拟合估计: 。
。
第三步:计算
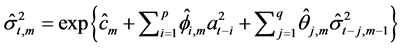
并且取 ,将估计值
,将估计值 返回到第二步,循环
返回到第二步,循环 次,当
次,当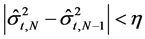 时停止循环,其中
时停止循环,其中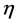 为充分小的正数。此时相应的复合分位数回归的最终估计记为
为充分小的正数。此时相应的复合分位数回归的最终估计记为 。则最终得到股票波动率的估计为
。则最终得到股票波动率的估计为
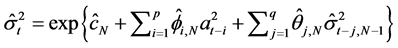
3. 实证分析
3.1. 样本选取和基本统计信息
本文研究对象为上海证券综合指数和深圳成分指数的收益序列。选取2000年1月28日到2011年12月30日的144个交易月末收盘数据。数据来源Sohu网页数据库(http://business.sohu.com/)。首先对两序列进行正态性检验。如下表1列出了两个收益序列的偏度、峰度以及Bera-Jarque检验统计量的结果。
由表1可以看出,两个序列均为正偏,这表明有较多的低于自身均值的收益率。另外其峰度值均大于3,表现出明显的尖峰厚尾性。统计量的检验结果在1%的显著性水平上拒绝了收益率序列的正态性假定。

Table 1. The basic information of returns of securities
表1. 证券收益序列的基本统计信息
3.2. 收益时序模型平稳性和条件异方差性检验
对上述上海综合指数和深圳成分指数的收益序列利用带有截距项不带趋势项显著性水平1%(T统计量临界值约为−3.4574)的ADF检验验证其平稳性。如表2所示两收益序数据均为平稳的。利用极大似然估计方法对上述两序列做非参数回归,通过反复对比观察,选取的相应非参数自回归模型拟合结果以及模型检验结果见表2。结果显示所有的残差序列平稳性检验显著,自相关和偏相关系数分析都没有截尾和拖尾存在。这表明利用非参数1阶自回归模型拟合该两收益序列是合适的。
另外,表2还给出了对两收益序列的残差序列的异方差性做LM-ARCH检验的结果。结果表明这两个收益序列均具有显著的条件异方差特性。对于有明显ARCH效应的扰动项我们利用2.3节提出的方法拟合波动率
3.3. 波动率的估计与评价
接下来对两个收益序列的残差序列分别用模型(4)和模型(7)建立GARCH模型,并且利用2.3节给出的复合分位数回归方法分别做估计。由于无法观测到真实的波动率,因此无法用估计的波动率与真实波动率进行比较。对此我们采用Peter和Alexander[8] 提出的量化指标来对比其优化程度:
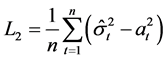
经过反复计算以及比较各类GARCH模型的AIC值,最终得出的结果是上海综合指数收益序列的差残差序列选取的模型滞后阶数为(1,1)时最优,深圳成分指数收益序列的差残差序列选取的模型滞后阶数为(2,1)时最优。如下表3给出了分别基于模型(4)与模型(7)的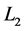 值,在复合分位数回归方法中,取分位点分别为
值,在复合分位数回归方法中,取分位点分别为 ,
,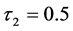 和
和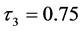 。由表3可以看出,相对于模型(4),基于模型(7)拟合波动率的逼近程度更高一些。另外还可以看出基于模型(4)与模型(7)利用复合分位数回归得到
。由表3可以看出,相对于模型(4),基于模型(7)拟合波动率的逼近程度更高一些。另外还可以看出基于模型(4)与模型(7)利用复合分位数回归得到 值都比较小,这也表明复合分位数回归可以有效的克服模型误差非正态影响,对异常值的敏感程度更低,是一种非常稳健的估计方法。
值都比较小,这也表明复合分位数回归可以有效的克服模型误差非正态影响,对异常值的敏感程度更低,是一种非常稳健的估计方法。
4. 结论
复合分位数回归方法是经典分位数回归方法的一个有意义的推广形式,该方法为计算时序波动率提

Table 2. The estimation of model parameters and the test of residual sequences
表2. 模型参数估计与残差序列检验
注:**表示在1%显著性水平下显著。

Table 3. The comparison of the two estimation methods based model (4) and model (7)
表3. 基于模型(4)与模型(7)的两种估计方法比较
供了一个新框架。基于复合分位数回归方法,可以直接对任意水平的条件分位点进行建模,而不依赖于特定的分布形式,更适合于厚尾分布数据的应用。本文选取GARCH模型的方差方程做对数变换,得到的模型用于估计股票收益波动率。这样不仅能保证模型误差的独立同分布性,而且在做对数逆变换后也能保证波动率的非负性。
另外,针对模型误差非对称性,本文利用更为稳健的复合分位数回归方法估计变换后的GARCH模型。实证分析表明,变换后的模型对波动率的估计更为有效。
基金项目
广西高校科研立项项目(2013LX147)。