1. 引言
自然界中,无论是简单的化学反应还是复杂的生命运动,都是由大量粒子组成的体系,实现着从无序到有序、从简单到复杂的各种变化,显示物质世界从无组织的混乱状态向不同程度的有组织状态的演变。这种演变过程就是我们通常所说的非线性过程,而正是由于这些非线性过程,才形成了物质世界的无限多样性、丰富性、曲折性、奇异性、复杂性、多变性和
演化性。化学振荡、化学波和化学混沌[1]作为化学学科中最经典的非线性化学现象已经成为近年来研究的热点。
2. B-Z化学振荡反应在分析检测中的应用
化学振荡分为规则振荡(振荡的周期和振幅基本上是不变的,即在一个振荡体系中只有一个固定的周期和振幅)和不规则振荡(即在一个振荡体系中有多个周期和振幅,包括混合模式振荡和混沌)。一个反应体系出现哪一种振荡模式取决于体系的控制参数的取值范围,B-Z振荡反应在不同的条件下就可以呈现规则振荡和不规则振荡,Strizhak从理论和实验两方面对混合模式振荡和混沌的研究做了大量工作[2,3]。
2.1. 规则振荡的应用
众所周知,一个化学振荡反应中包含着许多的基元反应,而当反应进行到不同阶段时所发生的基元反应是不一样的。如果在反应进行到某个阶段时候,向其中加入某种待测物质,若该待测物质与该阶段进行反应的某个反应物或者产物发生反应,那么必然影响该阶段的反应进行,并或多或少地影响以后发生的化学振荡反应。直接反映在振荡图形上就是周期和振幅的改变,随着加入干扰物的浓度不同,周期或者振幅的影响程度也不同。根据Taylor[4]对一些样品对体系的扰动机理的研究,一般认为还原性的物质以及大分子物质对体系的扰动比较明显。
当化学振荡反应进行到某一程度时,选择某一个周期进行进样,该周期我们将其称之为进样周期。该周期在没有进样时的周期和振幅分别标记为T0和A0,进样之后的周期和振幅分别标记为Ti和Ai。对于同一个规则振荡体系,在没有进样之前,只要各个底物的初始浓度,反应温度和搅拌速度不变,那么振荡图形基本是不会发生改变的,即T0和A0不变,这样就保证了实验的重现性和可靠性;同时,为了降低实验的系统误差,通常选择在同一个周期的同一个点进行进样,一般是图形的最高点或者最低点,而且每次进样的速度和体积恒定。随着加入样品量的不同,所得到的Ti和Ai也是不同的,通过一些简单的函数处理。例如T = Ti、T = Ti − T0、T = Ti/T0,A = Ai、A = Ai − A0、A = Ai/A0时,即可得到一组关于Ti和Ai的数据T和A,分别绘制T~C曲线和A~C曲线,在某一干扰物浓度区间内T~C和A~C呈线性关系,这就是规则化学振荡分析方法的理论基础。
在规则振荡中检测1-萘胺[5],当加入一定量的1-萘胺后,可以同时引起振荡周期和振幅的改变,如图1所示。Tichonva 首次用振荡反应作为分析检测的手段[6],在Ce4+催化的B-Z封闭体系中检测钌离子,具有很高的灵敏度和精确度(相对标准误差小于2.8%)。梁逸增等在振荡反应开始时加入干扰物质汞和铊,利
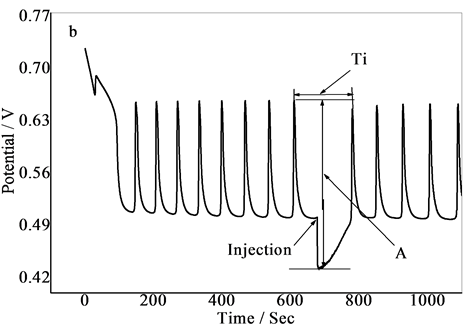
Figure 1. B-Z oscillation chemical reaction catalyzed by Ce4+ in a closed system
图1. 封闭体系中Ce4+催化的B-Z化学振荡反应图形
用其对周期的改变进行了分析检测。杨华等则研究了卤素离子对Ce4+催化的B-Z振荡反应的影响[7]。在封闭体系中,振荡反应由于与外界没有物质和能量的交换,振荡反应逐渐减弱直至停止。因此,封闭体系振荡反应在分析检测中的应用价值不是很大。
1995年,Jimenez-Prieto等报道了利用被检测物质对化学振荡体系的脉冲扰动进行分析测定[8]。其原理是对一个稳定的化学振荡体系,微量被测物的加入对原有化学振荡体系的振荡周期和其它参数有明显的改变,并且信号的改变与被测物的加入量呈线性关系,具有良好的精密度。这一研究使化学振荡在分析检测中具有真正的应用价值[9]。
2.2. 混沌的应用
所谓“混沌”原意指混乱、无序、未开化、不开通。混沌现象指的是自然界中那些不确定的、随机的、模糊的和复杂的状态与行为。
对于混沌运动,Lyapunov矩阵存在的实部根,表明此时轨道将按指数形式迅速发散,系统不具有稳定性,且对初始条件敏感[10]。因此,最大Lyapunov指数(IE)可以度量系统对初始条件的敏感性。
在非混沌系统中,相邻轨道一般是收敛的,或者是以小于指数形式的速率发散的。而在混沌系统中,相邻轨道是以指数形式发散的。正的Lyapunov指数对应本征矢量方向上的位移初始点,其发展出来的轨道会呈指数化分离趋势;在负的Lyapunov指数对应本征矢量方向上,相空间轨道会相互吸引趋近。因此,在非线性动力学系统的研究中经常将正的Lyapunov指数作为混沌是否出现的一个判据。
以下是利用混沌检测Cd2+离子的实验[11]。在诱导期加入样品,记录下进样点与第一周期结束的时间Ti(如图2)。待继续走完六个周期后,计算第二到第七周期的最大Lyapunov指数lL,加入不同浓度的Cd2+,所得到的Ti和lL是不一样的。将(lL·Ti)~lgC作图,便得到一条一定的范围内呈线性关系的工作曲线。
混沌方法的建立,很好地解决了规则化学振荡检测无机离子灵敏度低的问题,也从侧面说明了化学振荡方法的检测灵敏度还是可以再提高。虽然此方法的检测灵敏度较高,但方法比较抽象,对实验条件的要求也较高,在数据处理上需要专业的数学软件,限制了该方法的广泛应用,目前报道较少。
2.3. 非平衡定态(分叉)的应用
对于一个处于热力学孤立体系的化学反应来说,无论其初始状态如何,经过一段时间后最终总会达到平衡状态,即体系的熵值最大。换句话说,在热力学平衡态时,能够引起体系熵变的所有热力学“流”和热力学“力”均为零。对于一个非孤立体系,由于体系与环境之间存在有热力学“流”和热力学“力”的交换,则永远不可能达到热力学平衡状态,也就是通常所说的“处于远离热力学平衡态”。但如果外界施加的条件是固定不变的,体系在适应外界施加的条件时会发生相应的变化,最后还是可以达到一种“定态”,这种定态不是热力学平衡态,而是一种相对稳定的状态,只要外界施加的限制条件不发生变化,则这种稳定状态(通常称为非平衡定态)就可以一直维持下去。当一个化学反应体系处于远离平衡状态时,由于体系内多种非线性因素的相互作用,会出现丰富的时空有序的动力学行为,如:化学振荡、多重定态、化学混沌、以及在限制条件连续发生变化达到临界值时出现的分岔现象等。非平衡非线性系统的显著特点是对外界条件变化十分敏感,这一特性为分析检测应用提供了可能性。
最近,Vukojevic和Pejic等人[12,13]在考察B-L开放体系时指出,若逐渐改变外界施加于体系的限制条件,则规则振荡会转化为规则的分岔图形(如图3),两种振荡之间存在一个临界点,此时体系对外界的扰动最敏感。基于这一事实建立的分析方法灵敏度也非常高。利用分岔检测物质,首先要调整体系的参数,作
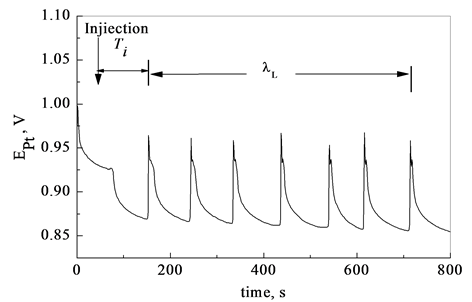
Figure 2. Determination of Cd2+ using Ce4+ catalytic oscillation of chaotic in a closed system
图2. 封闭体系中利用Ce4+催化混沌体系检测Cd2+的振荡图形

Figure 3. Bifurcation graphs by changing parameters
图3. 改变参数得到的分岔图形
出分岔图形然后在分岔点附近的振荡状态(非平衡定态)下进样,观察振幅的改变与浓度之间的关系,如图4。利用分岔的振荡行为检测物质具有仪器简单、操作简便及快速的优点。但是,对于其动力学行为及检测机理有待于进一步的研究。
3. 研究前景及展望
化学振荡反应的研究是一个处于化学、物理学、生命科学等多学科交叉点的前沿课题,其研究对解决生命起源等基本问题以及大气动力学、化工过程和化学过程分析等实际问题具有重大的影响。
由于化学振荡反应有其简单和易于实验研究的特点,而物理化学中的非线性非平衡无论是过去还是现在一直是许多科学家包括物理学家、化学家、生物学家以及应用数学家研究的热点。因此,开展化学振荡的研究不仅可以在化学理论与其有关的应用方面发现新的研究方向,而且可以促进化学和其他学科之间的相互渗透,更有意义的是对生命体内的变化得到进一步的认识。
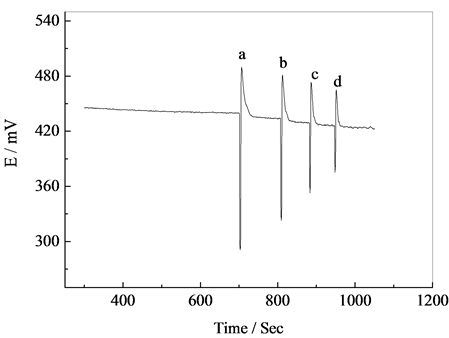
Figure 4. Classical oscillating profile
图4. 典型的扰动曲线
化学振荡在各个方面特别是在分析检测中的应用较多,由于振荡体系对各种物质的作用非常灵敏,因此,其在分析化学中的应用前景十分光明。而在其他方面的应用还需要进一步地研究。
目前,对化学振荡的不同振荡行为的研究,更加拓宽了其在分析检测中的应用,也为我们研究化学振荡开辟了一条新的道路。

NOTES
*通讯作者。