1. 引言
我国是地震多发国家，建筑结构在地震作用下的响应和抗震能力关系到人民生命财产的安全，地震作用是建筑结构分析设计中需要考虑的重要因素。地震作用对于建筑结构通常是循环往复作用，钢结构中的钢材在循环荷载下将出现如包辛格效应、循环硬化、循环软化、材料累积损伤等，这导致钢材在循环荷载下的性能不同于钢材在静荷载下的性能。
在地震的反复作用下，建筑钢材会产生损伤，钢材的累积损伤将对钢材的力学性能产生影响，当损伤积累到一定程度，材料和结构发生破坏。因此有必要对建筑钢材在反复荷载作用下的损伤进行研究。
在对Q225钢材进行的单调拉伸试验和反复加载试验的基础上，本文将对其他学者的多种损伤变量模型进行评述，并提出适用于Q225钢材的损伤变量。为研究低屈服点钢尤其是Q225钢材的循环加载性能以及考虑损伤累积影响的钢材本构关系提供基础。
2. 损伤变量评述
损伤变量是描述材料、构件或结构劣化程度的变量，一般定义为反应历程中某与损伤程度相关的累积量与相应的指标极限允许量的比[1] 。
基于退化的损伤变量，其损伤可用截面某种性质的减少来表达：
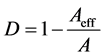(1)
式中，D为损伤变量，A为全截面面积，Aeff为有效截面面积。
基于变形的损伤变量，其变形变量包括构件的变形、应变和塑性率等，对于单质点体系的振动，采用如下方法：
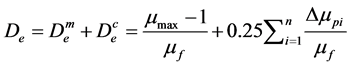(2)
式中，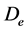
是振动结束时由N次循环塑性变形产生的损伤；
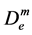是由最大变形产生的损伤；
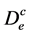是由循环塑性变形产生的损伤；m是塑性率，为塑性变形与屈服变形之比；
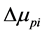是第i次循环的塑性率增量；
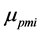是
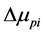的平均值；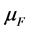
是单向变形破坏时的塑性率；
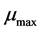是循环过程中的最大塑性率。
此外，基于变形和能量的损伤变量模型认为钢材在反复作用下的损伤变量D与所经历的塑性应变以及在循环荷载下的耗能有关。Park和Ang[2] [3] 基于一大批美国和日本的钢筋混凝土梁柱试验结果，提出钢筋混凝土构件的双参数地震损伤模型，从变形和滞回能耗散方面综合考虑，用规格化最大变形和规格化滞回耗能线性组合的形式来表示损伤变量D：
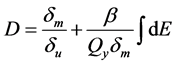(3)
式中，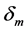
为实际荷载作用下最大变形；
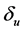为单调荷载作用下极限变形；
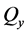为屈服强度；
为吸收滞回能量增量；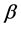
为非负参数。
该模型物理意义比较明确，并且经过试验和地震记录的检验，得到了工程界的认同。但也存在如下缺点：
(1) 单调加载时，D应为1，表示体系处于破坏极限状态，但是式(1)所示的Park和Ang模型在单调加载情况下，破坏时D > 1。
(2) 在弹性反应阶段，D应该为0，但是根据式(1)，D > 0。
针对Park和Ang模型上述不足，许多研究者提出了改进形式，包括以下几种。
(1) 沈祖炎等[4] 针对钢材的特性，提出了钢材在反复荷载作用下的损伤变量D：
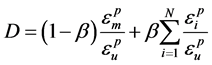(4)
式中：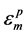
为钢材所经历的最大塑性应变；
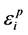为钢材
在第i次半循环中的塑性应变；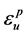
为钢材在一次拉伸时的极限塑性应变；β为权重系数，对于Q235钢，
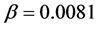；N为反复荷载的半循环周数。
(2) 欧进萍，牛荻涛等[5] 为分析地震作用下的钢结构破坏机理时，提出了如下表述的损伤变量D：
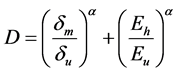(5)
式中，a是试验测定的参数，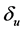
是层间弹塑性极限位移，
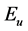是在单调加载下体系的滞回耗能，
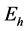是实际的累积滞回耗能。
2. Q225钢材损伤变量研究
2.1. Q225钢材单调拉伸试验和低周反复加载试验
单调拉伸试验的主要目的是了解此批钢材的一些基本性能，如弹性模量、屈服强度、极限强度和极限应变等。取自同一批25 mm厚Q225钢板，其出厂检验力学性能列于表1，沿轧制方向加工成6个试件，试件编号1、2、3作为试验件，4、5、6作为备用件。试验采用引伸计测量应变，引伸计标距50 mm，量程25 mm。试验机加载速率2 mm/min。试件尺寸如图1所示，实际构件如图2所示。试件装好后对中，再按加载速度加载直至试件断裂破坏。
反复加载试件来自同一批Q225钢材。共8个试件，取自25 mm厚Q225钢板，试件编号1#，2#，3#，4#作为试验件，5#，6#，7#，8#作为备用件，试件尺寸如图3所示，实际构件如图4所示。
各试件的具体加载制度如表2所示，加载方式采用应变控制，试验机应变加载速率为0.002 mm/mm×s−1。
2.2. Q225钢材试验结果和损伤变量模型
单调拉伸试验所测得的Q225钢材的弹性模量、屈服应力和断后伸长率情况如表3所示。
单调拉伸试验所测得三个试件的应力应变曲线如图5所示。
低周反复循环试件的破坏标准定为：最大拉力衰减20%且出现明显裂纹。四个试件破坏时循环圈数和用时如表4所示。
Q225钢材四个试验件的滞回曲线如图6所示。
在沈祖炎等[6] 提出的钢材在低周反复荷载作用下的损伤变量D模型的基础上，针对Q225的反复加载力学性能对权重系数β进行修正。
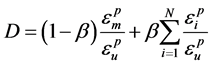(6)
Table 1. Mechanical properties of Q225 steel (provided by the manufacturer)
表1. Q225钢材力学性能(厂家提供)
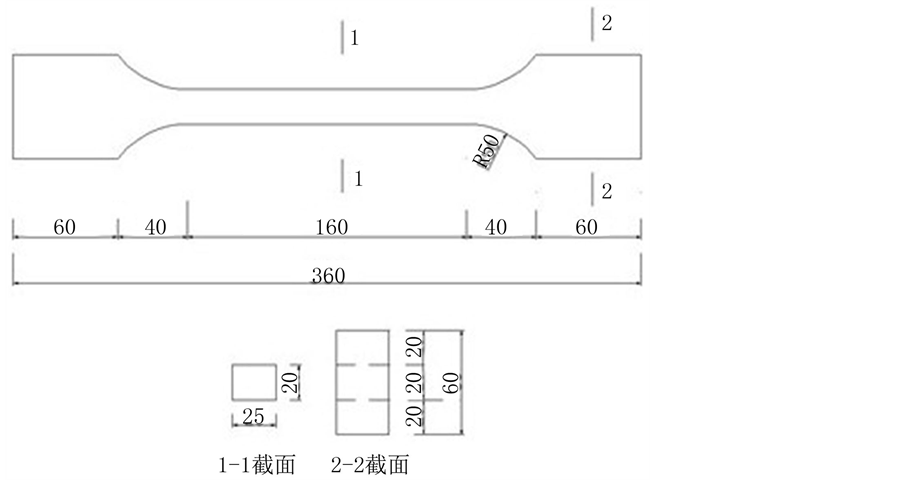
Figure 1. Size of specimen of Q225 under monotonic tensile tests
图1. Q225单调拉伸试件尺寸图
Figure 2. Practical specimen of Q225 under monotonic tensile tests
图2. Q225单调拉伸实际构件图
式中，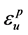
为钢材单调拉伸时的极限塑性应变，对于Q225，根据单调拉伸试验结果，可以取
。
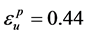Figure 3. Size of specimen of Q225 under repeated loading tests
图3. Q225反复加载试件尺寸图
Figure 4. Practical specimen of Q225 under repeated loading tests
图4. Q225反复加载实际构件图
Table 2. Cyclic loading system
表2. 低周反复加载制度
Table 3. Monotonic tensile test results
表3. 单调拉伸试验结果
Table 4. The number of cycles and the time used of lap when the Q225 specimen fails
表4. Q225试件破坏时循环圈数和用时
Figure 5. Q225 monotonic tensile stress-strain curves
图5. Q225单调拉伸应力应变曲线
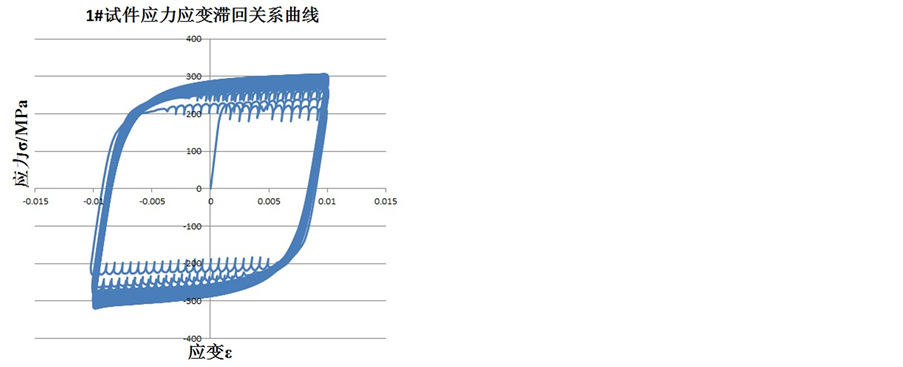
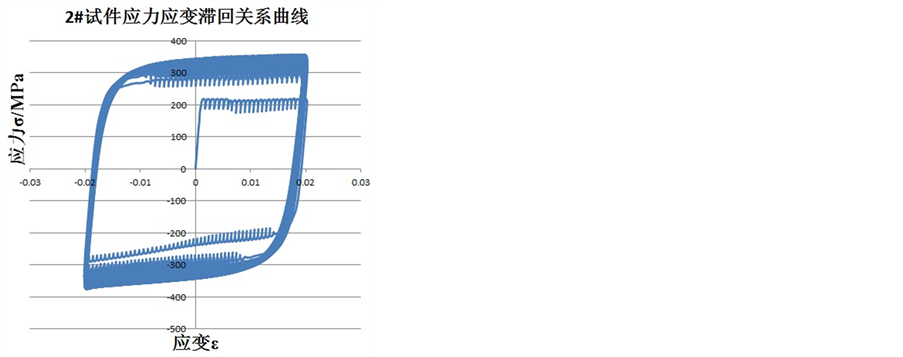
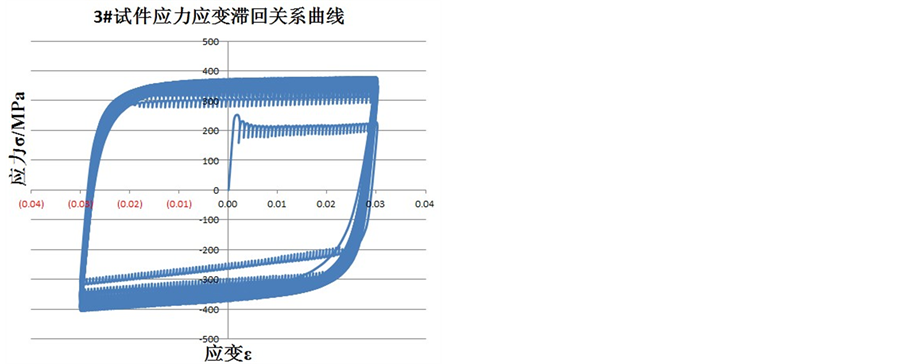
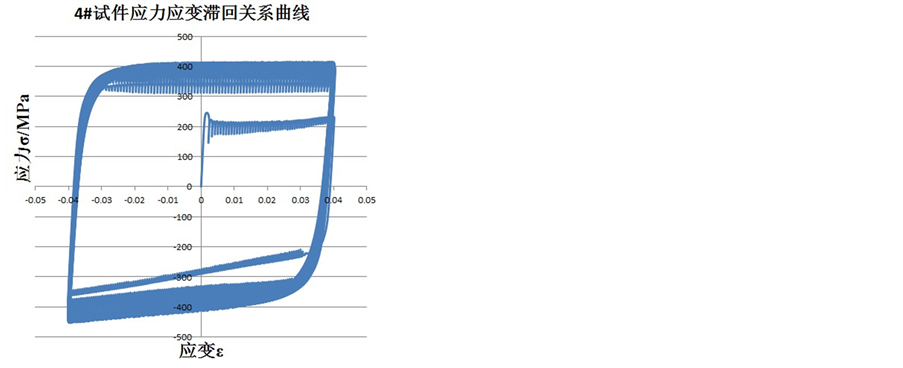
Figure 6. Hysteresis curves of Q225 steel specimen
图6. Q225钢材试验件的滞回关系曲线
对β取不同的值，可以得到不同的损伤变量计算值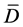
。根据损伤变量的物理意义，认为当试件破坏或者强度出现明显下降时，D = 1。根据最小二乘法，最优的β值应该使式(7)中的H最小，如图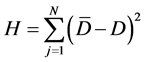7。
(7)
根据图中最小二乘法的计算结果，取β = 0.051，计算得到此时不同试件破坏时的损伤变量计算值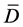
，列于表5中。从结果可以看出，四个试件根据β = 0.051计算得到的
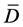均接近于理论值D = 1，可以证明取β = 0.051是合理的。
3. 结论
本文对不同的损伤变量模型进行了评述，根据Q225单调加载和低周反复加载试验结果，通过计算分析提出了适用于Q225低屈服点钢材的损伤变量模型：
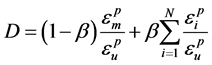(8)
式中，权重系数β = 0.051，其他参数的意义同前。
经验算，采用上述损伤变量模型时，试件破坏时的损伤变量计算值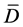
接近于理论值D = 1。证明对
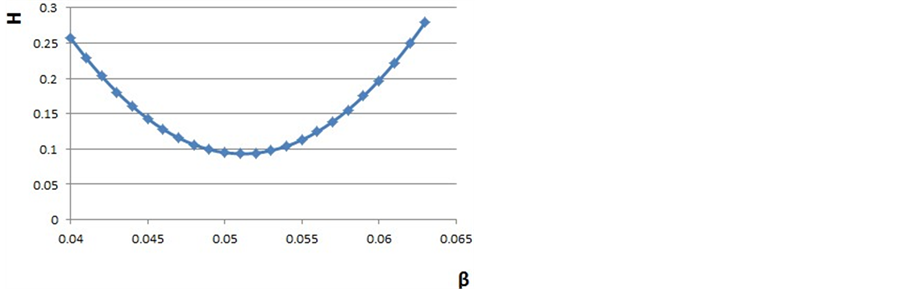
Figure 7. Values of H under different weighting factors β
图7. 不同权重系数β值下的H
Table 5. Calculation of damage variable parameter
表5. 损伤变量参数计算
Q225钢材，使用该损伤变量模型是对的。