摘要: 本文在已有的单变量Laguerre积分随机有限元方法的基础上,建立基于Laguerre积分的多变量随机有限元公式,提出了多变量Lagurre积分随机有限元方法(LISFEM)。利用ANSYS的APDL语言二次开发功能,将LISFEM嵌入到ANSYS软件当中,生成相应的计算程序模块,并利用ANSYS的后处理程序,实现随机结构的全节点应力和变形的均值和方差的云图显示。最后,以二回路中汽轮机叶片为例,选择不同的Laguerre积分点数目进行计算,并与解析解进行对比研究,计算结果表明该方法计算效率高,并且采用较少的积分点就能获得较高的计算精度,从而检验了该方法的正确性。
Abstract:
In the existing single variable Laguerre integral stochastic finite element method, based on Laguerre integral multivariate stochastic finite element formula, the author proposed variable Lagurre in- tegral stochastic finite element method (LISFEM). By using APDL of ANSYS, LISFEM was embedded into ANSYS, and corresponding calculation program module was generated, then using the post- processing program of ANSYS, the mean and variance of the whole node’s stress and deformation was realized by the cloud image displaying. Finally, took the turbine blade of the two loop as an example, chose different Laguerre integral point number and calculated, then compared with the analytical solution, the calculation results showed that the efficiency of calculating was high, and the less integral point could get high accuracy, so as to test the correctness of this method.
1. 引言
汽轮机叶片是汽轮机组的核心部件之一,叶片的寿命很大程度上影响着汽轮机的寿命。在实际运行过程中,汽轮机叶片的材料物性参数和转子所处的载荷环境,都具有一定程度的随机性。由于随机性的客观存在,对叶片的力学响应特性产生一定的影响。因此,本文将基于多变量Laguerre积分随机有限元方法对汽轮机叶片的随机响应特性进行研究,其对工程应用有着重要的理论价值和指导意义。
目前,研究不确定性结构的常用方法可分为两类:一类是统计的方法[1] -[3] ,就是通过大量的随机抽样,对结构反复进行有限元计算,最后对得到的结果作统计分析,这类方法称为Monte-Carlo随机有限元法,但该方法需要反复进行大量的模拟计算,针对大型复杂结构,并不适用。另一类方法[4] -[8] 就是以数学、力学分析作为工具,找出结构系统的响应与输入信号之间的关系,并据此得到结构应力或位移的统计规律,这类方法有:摄动随机有限元法、Neumann随机有限元法等。这类方法在大型复杂结构中的应用也非常有限。
本文考虑汽轮机叶片材料参数和载荷参数的随机性,设置了四种随机输入状态,利用多变量Laguerre积分随机有限元方法计算出了各输入状态下汽轮机叶片的最大应力和变形的均值和方差,同时与解析解作对比,通过误差分析,验证了多变量Laguerre积分随机有限元方法的正确性,并且通过编制程序实现了等直叶片的全节点应力和变形均值和方差计算。
2. 多变量Laguerre积分随机有限元方法
在实际的随机结构中,一般都存在多个随机变量,在多个随机变量等因素影响下,结构的随机分析有较大的难度。因此,多随机变量的结构分析,尤其是针对复杂结构的随机分析是当前随机有限元领域中一个重要而且困难的问题。
设X为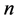 维随机向量,
维随机向量,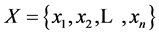 ,其均值
,其均值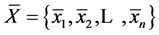 ,令
,令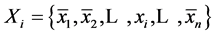 ,即
,即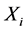 中除了
中除了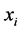 外,其余的随机变量为其均值。其中,响应
外,其余的随机变量为其均值。其中,响应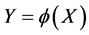 的统计量如下方法获得。
的统计量如下方法获得。
取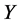 的近似表达式为
的近似表达式为
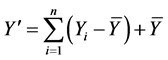 (1)
(1)
式中: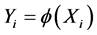 ;
;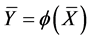 。则
。则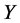 的统计量可由其近似量
的统计量可由其近似量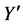 导出。
导出。
均值
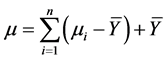 (2)
(2)
方差
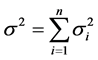 (3)
(3)
3阶中心矩
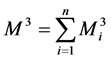 (4)
(4)
4阶中心矩
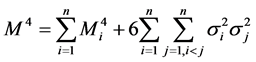 (5)
(5)
5阶中心矩
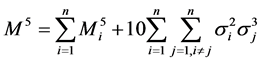 (6)
(6)
6阶中心矩
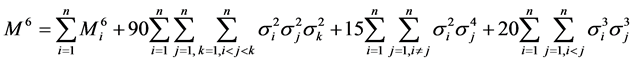 (7)
(7)
其中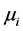 、
、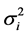 是分别按照单变量Laguerre积分随机有限元列式[9] [10] 来计算。
是分别按照单变量Laguerre积分随机有限元列式[9] [10] 来计算。
3. 积分随机有限元方法嵌入ANSYS
ANSYS具有很好的二次开发功能,主要的二次开发工具有四种,分别是APDL语言、UIDL界面设计工具、UPFs用户程序和数据接口。利用APDL语言编写积分随机有限元方法的用户程序,只需开发2个程序模块就可实现随机有限元分析的全过程。下面介绍各个模块的功能。
模块一:计算分析模块,首先定义随机变量,输入计算所要求的积分点数目,并读入各个积分点数值及相应的权重,然后反复调用确定性有限元进行求解,循环次数即为积分点数目,最后把所有节点的求解结果保存到一个m×n的矩阵当中,m为分析对象的节点总数,n为积分点数目。
模块二:结果分析模块,根据求解结果矩阵,利用上节所给出的积分方程计算出结构响应随机变量在所有节点的各阶中心矩、偏度系数和峰度系数,最后通过ANSYS后处理模块显示结果。
4. 汽轮机叶片的随机响应分析
以等直叶片为研究对象,其中,叶片的数据如下:长度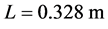 ,截面形状为矩形,宽度
,截面形状为矩形,宽度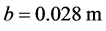 ,安装角为0,轮盘半径
,安装角为0,轮盘半径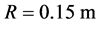 ,弹性模量均值为
,弹性模量均值为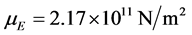 ,变异系数
,变异系数 ,密度均值为
,密度均值为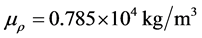 ,变异系数为
,变异系数为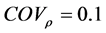 ,离心力载荷,叶片绕x轴旋转,转速均值
,离心力载荷,叶片绕x轴旋转,转速均值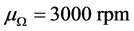 ,变异系数
,变异系数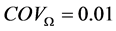 。等直叶片的模型如图1所示,具体参数如表1所示。
。等直叶片的模型如图1所示,具体参数如表1所示。
设定等直叶片的弹性模量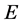 、密度
、密度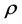 和角速度
和角速度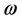 为随机输入变量,等直叶片的最大应力和变形为随机输出变量。采用间隔取值,通过等概率变化式,分别对积分点数目为2、6、10时Laguerre积分点及相应的权重进行变换计算,其中,变换后的密度
为随机输入变量,等直叶片的最大应力和变形为随机输出变量。采用间隔取值,通过等概率变化式,分别对积分点数目为2、6、10时Laguerre积分点及相应的权重进行变换计算,其中,变换后的密度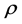 的积分点和相应权重如表2所示。
的积分点和相应权重如表2所示。

Figure 1. Straight blade model

Table 1. Variable parameter
图1. 等直叶片模型
表1. 变量参数

Table 2. Integral point and weight after density transformed
表2. 密度变换后的积分点及权重
在随机输入变量分别为弹性模量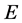 、密度
、密度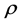 、角速度
、角速度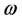 和三个变量同时作用四种随机输入情况下,根据上节所推导的积分随机有限元计算公式,分别计算当积分点数目为2、6、10时等直叶片的应力和变形响应的均值和方差,并利用ANSYS的二次开发语言—APDL进行编程,将积分随机有限元方法嵌入ANSYS软件当中,最后用ANSYS的后处理显示计算结果。
和三个变量同时作用四种随机输入情况下,根据上节所推导的积分随机有限元计算公式,分别计算当积分点数目为2、6、10时等直叶片的应力和变形响应的均值和方差,并利用ANSYS的二次开发语言—APDL进行编程,将积分随机有限元方法嵌入ANSYS软件当中,最后用ANSYS的后处理显示计算结果。
为了节约篇幅并且方便观察,在此只列出积分点数目为10时,随机输入变量为密度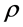 的情况下等直叶片的应力和变形的均值和方差分布云图,分别如图2~5所示。
的情况下等直叶片的应力和变形的均值和方差分布云图,分别如图2~5所示。
表3列出了积分点数目为10时,四种随机输入情况下等直叶片的最大应力和变形均值,并与解析解作对比,表4列出了积分点数目为10时,四种随机输入情况下等直叶片的最大应力和变形方差,同时也与解析解作对比,通过误差分析,验证了Laguerre积分随机有限元方法的正确性,并且通过编制程序实
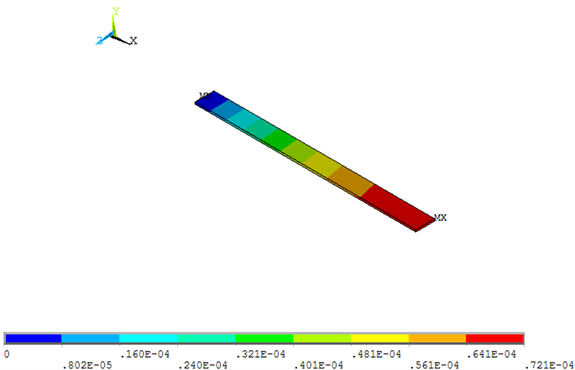
Figure 2. The mean deformation’s image of the straight blade
图2. 等直叶片的变形均值云图
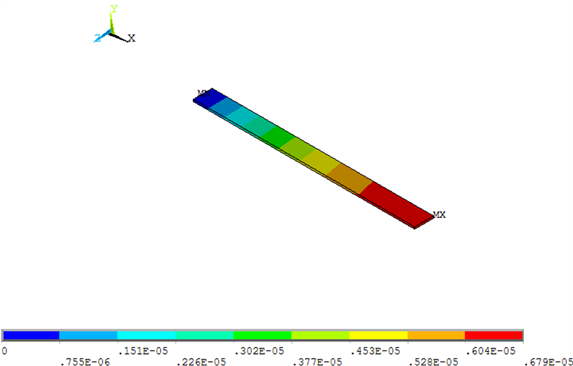
Figure 3. The variance of deformation’s image of the straight blade
图3. 等直叶片变形方差云图
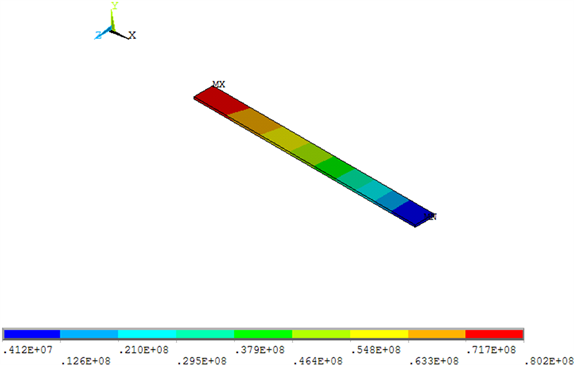
Figure 4. The mean stress’s image of the straight blade
图4. 等直叶片的应力均值云图
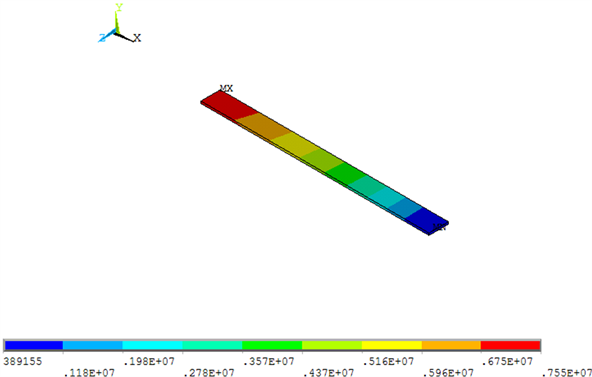
Figure 5. The variance of stress’s image of the straight blade
图5. 等直叶片的应力方差云图

Table 3. The mean of the maximum stress and deformation