大牛地气田盒3气藏使用套压计算无阻流量的新方法

A New Method of Calculating the Open Flow Using the Casing Pressure in Daniudi Gas Field H3 Gas Reservoir

摘要: 本文从井筒流体力学出发，利用平均温度和平均气体偏差系数方法计算了大牛地气田盒3气藏6口井70组井底流压数据，通过分析认为可以使用该方法计算盒3气藏单采井的井底流压。进一步通过回归分析的方法构建了盒3气藏单采井的流压关于套压的线性关系式，确定了现场使用套压计算无阻流量的新方法。在求取无阻流量的过程中，该方法具有测试数据少，工序简单的特点。

Abstract: From the wellbore fluid mechanics, the 70 wellbore pressures of 6 wells in the H3 gas reservoir in Daniudi gas field were calculated by using the average temperature and the average gas deviation factor method in this paper. The results showed that this method can be used for calculating of the wellbore pressure, and then the linear relation between the casing pressure and the wellbore pressure was constructed by regression analysis method. This method has the advantages of simpler procedure and fewer test data in the process of calculating the open flow.

1. 引言

国内许多学者和现场技术人员在大牛地气田气井的无阻流量求取方法和过程中做了大量的工作[1] -[4] ，这些方法都是基于一点法试井理论，按照一点法试井作业流程与要求进行测试数据。这些方法要求测试达到稳定状态，同时井底流压还须满足一定界限，若气井产量过大等，都会造成计算结果误差较大。本文从井筒流体力学出发，计算了70组井底流压数据，建立了使用套压计算无阻流量的公式，结果认为该公式在求取无阻流量的过程中具有要求测试数据少，工序简单等特点。

盒3气藏主要位于大牛地气田的西南部，为大牛地气田的主力气藏。其古沉积环境具有地形高差小、坡度缓 、物源充足等特点。发育具有典型河流冲积特征的河流相沉积体系，具有隔夹层发育，非均质性强的特点[1] [2] 。孔隙度分布在4.8%~12%之间，渗透率分布在(0.101~2.14 × 10⁻³) μm²之间，属于典型的低孔低渗储层[3] [4] 。

大牛地气田盒三气藏2002年获高产工业气流，2003年开始投入开发，2005年进入全面开发阶段。截至2010年11月10日该气藏共投产单采井175口，其中稳产井96口，非稳产井79口。截至2010年11月10日该气藏单采井平均日产水量为0.12 m³。

2. 计算井底流压方法简介

当井内为纯气柱时，利用平均温度和平均气体偏差系数计算井底压力的公式为[5] [6] ：

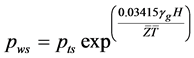(1)

式中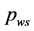：——按静止气柱公式计算的井底压力。关井时为地层压力，开井时为井底流动压力，MPa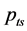；——静止气柱的井口压力。关井时为井口最大关井压力，开井时为不流动气柱的井口压力，MPa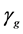；——气体相对密度，无因次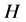；——井口到气层中部深度，m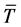；——井筒内气体平均绝对温度，K；

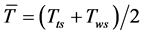(2)

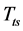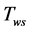、——静止气柱井口、井底绝对温度，K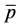；——井筒气体平均压力，MPa；

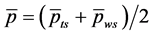(3)

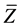——井筒气体平均偏差因子，无因次，有两种计算方法：

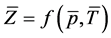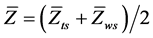或(4)

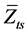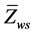、——静止气柱井口、井底条件下的气体偏差系数。

3. 流压与套压的关系

3.1. 井底流压计算

统计了71口井天然气的相对密度计算其平均值为0.58，47口生产井2005年的井筒平均温度为49.77℃(322.92 K)，25口2006年投产井的井筒平均温度为49.29℃(322.44 K)，32口2007年投产井的井筒平均温度为48.82℃(321.97 K)，18口2008年投产井的井筒平均温度为48.15℃(321.30 K)，27口2009年投产井的井筒平均温度为47.19℃(320.34 K)。35口生产井的气体平均偏差系数为0.98。将以上参数带入式(1)，得到盒三气藏采用定产降压生产方式的6口单采井的70组井底流压数据。

3.2. 误差讨论

70组绝对误差如图1所示，其最大值为3.33 MPa，平均值为0.35 MPa，中值为0.06 MPa。其中有60个正值，10个负值，最小值为−3.21 MPa。由于实际井筒中有积液存在，根据静止气柱计算的井底压力理论值要小于实际测量的井底流压值，即实测流压与计算压力值之间只能存在正值误差，故认为在误差分析中应该忽略10组有负误差值的数据。另外分析图1中绝对误差值的趋势，可以看出在正值误差中最大值(3.33 MPa)是比较异常的，故在误差分析中予以忽略。

对剩下的60组绝对误差数据进行统计分析，最小值为0.01 MPa，最大值为1.35 MPa，平均值为0.43 MPa，中值为0.68 MPa。其中在0到0.5之间的有38个，占统计井数的63.33%，大于1的只有3个。相对误差数据如图2所示，最小值为0.0043%，最大值为8.99%，平均值为2.60%，中值为4.49%，所有值都小于10%。综上认为，此方法在大牛地气田盒3气藏是适用的，可以用来计算井底流压。

3.3. 流压关于套压关系的确定

对60组流压和套压数据进行线性回归分析(如图3所示)，得到流压关于套压的回归方程为：

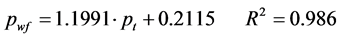(5)

Figure 1. Flow pressure absolute error

图1. 流压绝对误差

Figure 2. Flow pressure relative error

图2. 流压相对误差

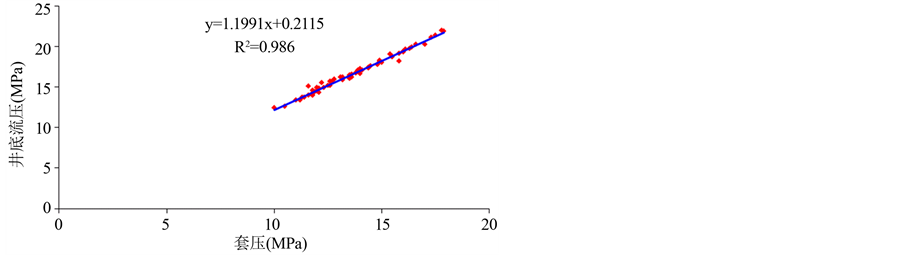
Figure 3. Flow pressure on casing pressure regression analysis

图3. 流压关于套压回归分析

该式定量的解决了套压和流压之间的关系，从相关系数来看二者之间具有很好的的线性相关关系。

4. 利用套压确定无阻流量的方法

4.1. 公式推导

现场一点法试井计算无阻流量使用的经验公式如下[3] [4] ：

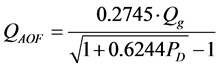(6)

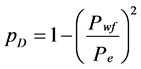(7)

式中：Q_g——气产量，m³/d；P_wf——井底流动压力，MPa；P_e——原始(或平均)地层压力，MPa；P_D——无因次压力，无因次；Q_AOF——无阻流量，m³/d。

将(5)式代入(7)式得到无因次压力计算公式：

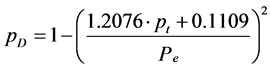(8)

这样将(6)式和(8)式联立就建立了现场使用套压计算气井无阻流量的新方法，使用该方法求取气井无阻流量只要求测试套压和稳定气产量，具有工序简单的特点。

4.2. 实际应用

统计了30口盒3气藏单采井的试井期间的稳定气产量、井底流压、井口套压和无阻流量，使用实测地层压力值和平均底层压力值应用(6)式和(8)式计算30口单采气井的无阻流量，做无阻流量的绝对误差分析柱状图(如图4)和相对误差分析柱状图(如图5)。从图4可以看出，测试解释无阻流量值与使用实测地层压力计算无阻流量值之间的绝对误差最大值为3.28 × 10⁴ m³/d，最小值为−4.76 × 10⁴ m³/d，平均值为0.04 × 10⁴ m³/d，中值为−0.74 × 10⁴ m³/d，在(−1~1) × 10⁴m³/d之间的有26口井，占计算井数的87.00%。测试解释无阻流量与使用平均地层压力计算无阻流量之间的绝对误差最大值为4.90 × 10⁴ m³/d，最小值为−6.44 × 10⁴ m³/d，平均值为0.07 × 10⁴m³/d，中值为−0.77 × 10⁴ m³/d，在−1到1之间的有21口井，占计算井数的70%。

从图5可以看出，测试解释无阻流量值与使用测试地层压力计算无阻流量值之间的相对误差最大值13.98%，最小值−10.72%，平均值0.73%，中值1.63%，相对误差在−10%～10%之间的有23口井，占计算井数的90.00%。测试解释无阻流量与使用平均地层压力计算无阻流量之间的相对误差最大值53.64%，最小值−29.29%，平均值1.32%，中值12.18%，相对误差在−10%～10%之间的有20口井，占计算井数的66.67%。

使用实测地层压力和平均地层压力计算的无阻流量的绝对误差在(−1~1) × 10⁴ m³/d的占总井数的比例分别为80%和70%，相对误差在−10%~10%之间的占总井数的比例分别为90%和66.67%。从绝对误差和相对误差的情况来看，大部分井计算结果的精度较高，能够满足现场施工需要。综上分析，使用井口套压计算气井无阻流量的精度较高，在现场是切实可行的。同时，使用实测地层压力计算的无阻流量精

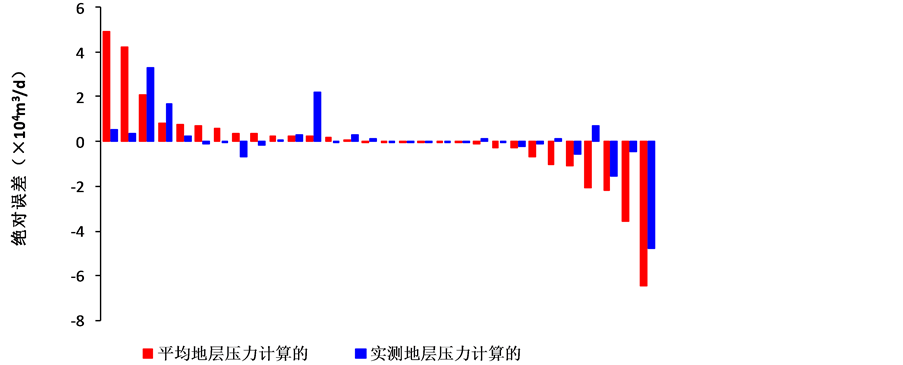
Figure 4. Open flow absolute error analysis

图4. 无阻流量的绝对误差分析

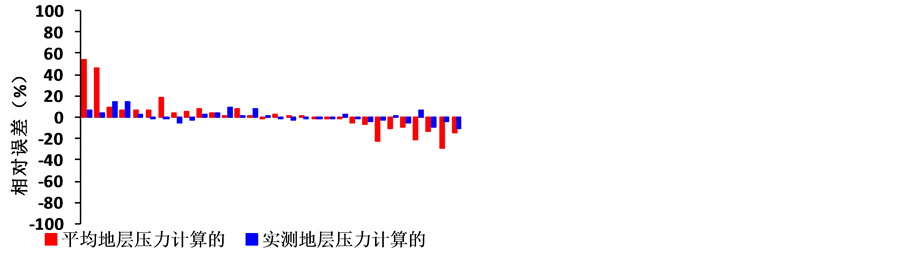
Figure 5. Open flow relative error analysis

图5. 无阻流量的相对误差分析

度要高于使用平均底层压力计算的结果，但使用平均地层压力计算无阻流量的方法对现场测试要求较低，不要求进行停产测试。

5. 结论

1) 井底积液较少的气井可以使用井口套压数据，根据平均井筒温度和平均气体偏差系数计算方法求取井底流压。

2) 大牛地气田盒3气藏单采井的井底流压与井口套压数据之间具有很好的线性关系，即。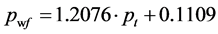

3) 使用井口套压数据计算无阻流量的方法，具有较高的计算精度，可以满足现场工程精度需要，同时具有不影响单井正常生产的优点。