1. 引言
IPCC对全球气候变化发布的第5次评估报告中表示：全球气候变化不同程度地改变和正在改变区域降水量、蒸发量，从而影响了水循环过程，驱动了径流量等水文要素的变化，改变了区域水量平衡[1] 。随着经济迅速发展，人类活动对生态环境造成的破坏日益显现，如水资源污染及浪费、温室效应、植被退化等。在全球气候变化和人类活动的影响下，下垫面的能量和水分循环特征发生了很大变化，使得用于水文频率分析的系列的概率分布或统计规律发生了变化，水文序列的样本已经不满足传统水文频率分析的一致性前提和要求，在变化环境下基于传统水文频率分析得出的结果存在失真风险。因此，变化环境下水文序列的非一致性频率分析的研究十分重要。近年来非一致性水文序列的频率分析成为国内外学者关注的研究课题。
对非一致性水文序列进行频率分析，国内采用较多的方法是基于还原途径的水文频率分析法[2] 。这种方法主要包括：变异点前后系列与某一参数的关系分析法、时间序列的分解与合成方法以及水文模型方法3种。韩瑞光[3] 采用关系分析法，选取海河流域若干代表站，通过建立不同时期代表站控制流域面平均年降雨量与年径流量之间的关系，对年径流系进行了一致性修正，并应用分布式水文模型研究了不同下垫面条件下的径流量及其变化趋势。谢平等[4] 采用时间系列的分解和合成方法，对潮白河的年径流系列进行了研究，得到潮白河过去、现在和未来年径流的频率分布，分析了北京市的水资源安全问题。王国庆等[5] 以黄河中游三川河流域为例，采用流域水文模型模拟了20世纪70年代后的天然径流过程，定量评估了气候变化和人类活动对流域径流的影响。国外研究较多的方法是基于非一致性极值系列直接进行水文频率分析，成果主要集中在以下三方面：基于混合分布的非一致性水文频率分析方法、基于时变矩的非一致性水文频率分析方法和基于条件概率分布的非一致性水文频率分析方法。Waylen和Woo[6] ，Diehl和Potter[7] 及Singh和Sinclair[8] 等假设非同分布的极值样本序列是由若干个子分布混合而成的，从而构建混合分布模型对非同分布的极值样本序列进行频率分析。Strupczewski等[9] -[11] 提出一个非一致性极值系列的频率分析模型，该模型是将趋势性成分嵌入到分布的一、二阶矩中(时变矩)，即考虑统计参数均值和方差的趋势性，基于时变矩对水文序列进行频率分析。在基于条件概率分布的非一致性水文频率分析方法方面，Singh[12] 认为洪水频率分析的适线法不适合用来计算非一致性洪水序列，他们提出了一种全新的估计非一致性洪水序列中特大洪水的超过值概率的方法。
淮河是中国9大河流之一，流域内地质地貌、水文气候和社会经济条件复杂[13] 。全流域共修建大中小型水库5700多座，其中大型水库36座，流域内还修建了各类水闸5000多座，其中大型水闸约600座[14] ，在这些闸坝的调控下，淮河流域已经不是天然径流状况，而是受到人类活动的严重影响，再加上气候变化的影响，水文序列属于非一致性序列。若要对水文序列进行频率计算，推求出洪水的设计标准，保证区域水资源安全，就不能简单地使用传统的频率计算方法，必须考虑序列的变异情况，用非一致性序列的水文频率计算方法进行计算。在目前的研究中，对淮河流域的水文序列进行变异分析以及基于非一致性序列进行频率计算还比较少。因此，本文综合考虑淮河流域的情况，以淮河流域大坡岭和鲁台子站点的年最大洪峰序列为例，对序列进行趋势性和跳跃性诊断，然后基于还原途径对非一致性序列进行频率分析。研究可以提高该地区所求洪水设计值的精确度，为各种涉水工程的设计、规划、施工以及区域水资源管理提供科学依据，保证工程安全区域水安全。
2. 研究区域和研究方法
2.1. 研究区域
淮河流域以南属亚热带，以北属暖温带，处于湿润区向半干旱区的过渡地带，导致了淮河流域水资源时空分布不均匀。它还介于长江和黄河两大流域之间，再加上黄河时有夹杂着大量泥沙倾入淮河的情况发生，致使淮河流域形成典型的孕灾环境。此外，流域多年平均年降水量883 mm，年降水量的地区变幅为600~1400 mm，降雨主要是受夏季风影响，多集中在汛期的5~8月(淮河上游和淮南)或者6~9月(其它地区)[13] 。这种年际变化大，年内分布不均的降雨情况，成为淮河流域洪水灾害频发的一个重要原因。淮河流域特殊的气候条件加之人类活动的影响构成了破坏下垫面条件稳定性的重要原因。
本文选取了淮河流域干流上游的大坡岭站及中游的鲁台子站点进行分析。将两个站点从1956年~ 2010年的日径流量资料进行选样，得出两个站点的年最大洪峰序列，然后分别对两个序列分别进行相关研究(图1)。
2.2. 研究方法
2.2.1. 变异诊断方法
由于受水文循环、自然条件和人类活动的影响，水文情势在时间上或空间上往往会发生变异[15] 。为了识别这种非一致性的水文序列，需要对其进行变异分析诊断。
本文选取相关系数检验法[16] 、斯皮尔曼(Spearman)秩次相关检验法[16] 和肯德尔(Kendall)秩次相关检验法[16] 对水文序列进行了趋势性诊断。相关系数检验法的实质是利用最小二乘法对水文时间序列进行线性拟合，用相关系数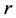
来检验水文特征值与其对应时序是否存在显著的相关关系，给定显著性水平
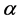，如果相关系数
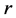满足
(
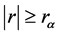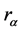为给定的显著性水平
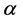所对应的相关系数临界值)，则认为线性趋势存在，否则线性趋势不存在；斯皮尔曼秩次相关检验法的实质是对水文序列的序列值进行排序，检验序列值的
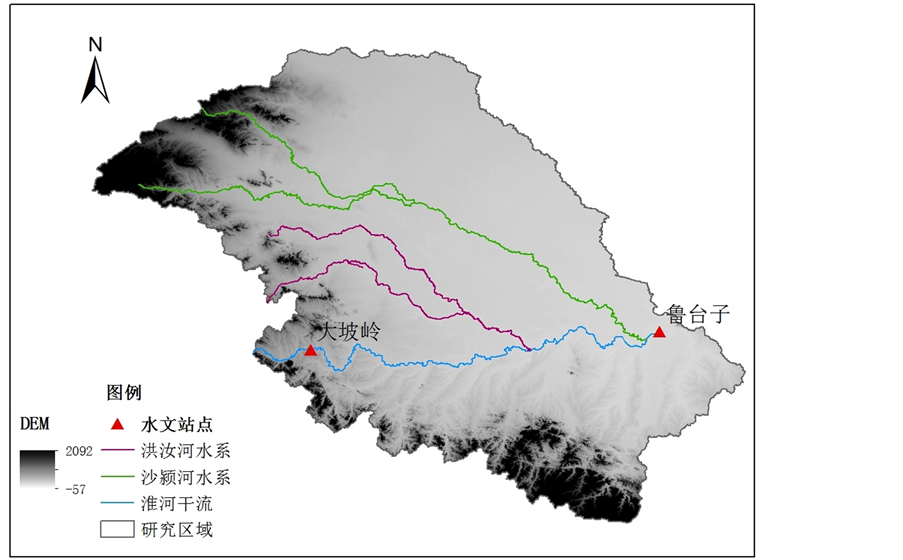
Figure 1. The location map of study sites
图1. 研究站点位置图
秩次与其对应时序的相关程度，如果序列值的秩次与时序越相近，则秩次相关系数越大，趋势越显著，对秩次相关系数是否已于零采用T检验法，取显著性水平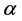
，若
，则判定序列趋势性显著，否则趋势性不显著；肯德尔秩次相关检验法的实质也是检验序列值与时序的相关程度，采用U统计量进行趋势性检验，给定显著性水平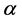
，若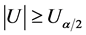
，则趋势性显著，否则不显著。
本文选取有序聚类法[17] 、最优信息二分割法[18] 和滑动T检验法[17] 对序列进行跳跃性诊断。有序聚类法的本质是求取最优分割点，使同类之间的离差平方和最小，在所有分割点中，使得分割前后两个序列的离差平方和相加得到的总离差平方和最小的点为最有可能的变异点；最优信息二分法的实质是通过构造比较序列和计算差异信息的相对测度(或差异幅值)来检验序列的变异性，将所有可能变异点所对应的差异幅值进行绘图，若图像变化平缓，无明显的波谷存在，即水文序列无变异点，若图像变换有平缓段和剧烈段，且波谷明显，即水文序列存在变异点，变异点即为波谷点；滑动T检验法的实质是构造服从T分布的检验统计量，判别分割点前后的两个序列的差异性，取显著性水平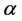
，若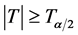
，则判定该分割点前后两个序列存在显著性差异，否则差异不显著。
由于各种方法在原理和判别方法上都有所不同，因此最后的诊断结果也可能有所差异，在下文分别用三种方法进行趋势诊断和跳跃诊断时，将选取两种或两种以上方法的共同结果作为最终检验结果。
2.2.2. 非一致性水文频率计算方法介绍
本文选取时间序列的分解与合成方法对非一致性序列进行频率计算。根据水文时间序列的线性叠加原理，假设非一致性水文时间序列由相对一致的随机性成分和非一致的确定性成分两部分组成，通过对确定性成分的拟合来反映过去、现在和未来条件下的环境变化，通过对随机性成分的频率计算来反映水文时间序列的统计规律。
1) 非一致性水文时间序列的分解
根据水文时间序列的变异综合诊断结果，若非一致性水文时间序列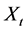
的变异点为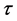
，则表明变异点
分割后的前后两个序列，其物理成因是不相同的。变异点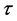
之前序列的主要成分为随机性成分，而变异点
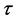之后序列的则包含随机成分和确定性成分两部分，用数学方程可表示为：
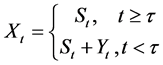(1)
式中，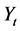
为非一致性的确定性成分；
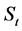为一致性的随机成分。若序列为趋势变异，则
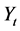是时间t的函数；若序列为跳跃变异，则
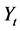为常数；若序列既有趋势变异又有跳跃变异，则
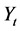是时间t的分段函数。
当水文序列扣除趋势和跳跃成分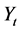
后，剩余的成分可看作是纯随机成分。对于水文序列
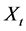中的纯随机成分
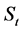，可以采用现行的水文频率计算方法进行频率计算，这样就得到了非一致性水文序列中的随机性规律。
2) 非一致性水文时间序列的合成
非一致性水文时间序列分解的目的是要推求序列中各种成分的规律；而合成的目的则是预测或者评估由“时间域”中的确定性成分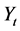
与“频率域”中的随机性成分
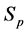合成后的水文时间序列
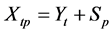。本文选取分布合成法对序列进行合成。
我国学者谢平[19] 等人提出了一种集合数值合成、参数合成于一体的分布合成方法。首先根据非一致性水文序列的确定性规律和随机性规律，利用蒙特卡洛法随机生成某个时间的样本序列；然后采用现行的水文频率计算方法求得该样本序列满足皮尔逊Ⅲ型频率分布的统计参数：均值EX，变差系数Cv和偏态系数Cs，从而得到非一致性水文序列的合成分布规律；最后根据合成分布规律，解决两类水文频率计算问题。
用蒙特卡洛法随机生成某个时间的合成样本序列可以分为下面三个步骤：
1) 根据确定性规律预测某个具体时刻的确定性成分；
2) 利用蒙特卡罗法生成满足皮尔逊Ⅲ型频率分布的纯随机序列；
3) 将确定性成分与随机性成分进行数值合成，得到合成后的样本序列，从而推求合成分布及其参数。
3. 研究结果及讨论
3.1. 变异诊断结果
本文首先对大坡岭和鲁台子的最大洪峰序列进行趋势诊断(显著性水平为0.1)，结果如表1所示。
由表中结果可知：大坡岭站和鲁台子站的年最大洪峰序列均未发生趋势变异。
接着基于有序聚类法、最优信息二分法和滑动T检验法分别对两个站点的最大洪峰序列进行跳跃性检验，如图2、图3所示。
对于大坡岭站，滑动T检验法的图可以分析出：在显著性水平0.1下，1981年超过了临界值，且有序聚类法同样检验出该站点于1981年发生变异，说明大坡岭站的年最大洪峰序列在1981年发生跳跃变
Table 1. The trend diagnosis results of the hydrological series
表1. 水文序列的趋势诊断结果
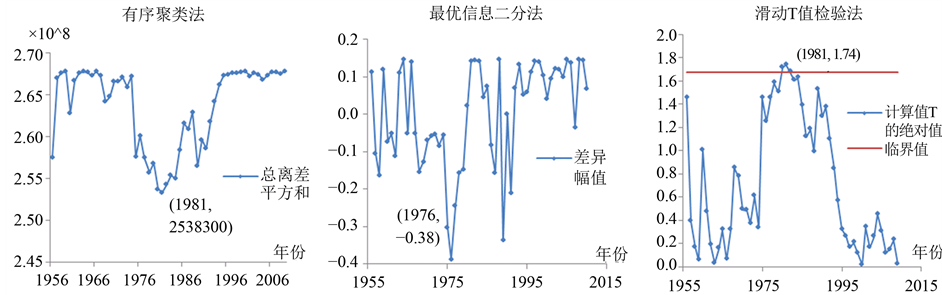
Figure 2. The jumping diagnosis results of the annual maximum flood peak series of Da Po Ling station
图2. 大坡岭站洪峰序列的跳跃性诊断结果
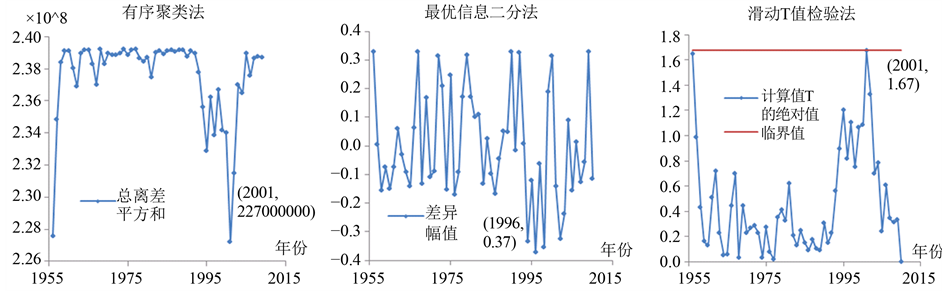
Figure 3. The jumping diagnosis results of the annual maximum flood peak series of Lu Tai Zi station
图3. 鲁台子站洪峰序列的跳跃性诊断结果
异，同理可知，鲁台子站的年最大洪峰序列在2001年发生跳跃变异。
变异的成因分析：自1978年邓小平提出改革开放的新政策以后，我国对工业化战略作出了调整。由于沿淮经济技术水平和产业层次都相对比较低，因此淮河流域的工业迅速发展。工业的发展对淮河流域的下垫面条件造成了很大的改变。除此之外，卢燕宇等人[20] 研究表明，淮河流域年降水量变化具有明显的阶段性，在1960~1990基本为下降趋势；而在2000年后，降水量上升十分明显。这也就不难解释为何淮河流域大坡岭站的洪峰序列在1981年发生了向下跳跃变异。
高超[21] 等人研究表示，淮河流域年平均气温在20世纪90年代以前以降温为主，90年代中后期增温显著。且在2000年左右，淮河流域受西北太平洋副热带高压异常偏强，加之西南暖湿气流强盛，导致冷暖空气在淮河流域交汇，降水量异常偏多。因此，鲁台子站的洪峰序列在2001年向上跳跃是符合实际情况的。
3.2. 非一致性序列的频率计算结果
将大坡岭和鲁台子站年最大洪峰序列的跳跃成分的计算和扣除结果列入表2，将过去条件下及现状未来条件下序列的皮尔逊Ⅲ型频率分布的统计参数列入表3。
将两个变异序列在过去、现状和未来条件下(对于跳跃变异而言，序列在现状和未来条件下的频率计算结果相同)的频率计算结果绘制在图中进行对比，如图4，图5。
由上述两张图可以看出，大坡岭站相同频率的洪峰流量序列在现状和未来条件下减小的迹象，而鲁
Table 2. The calculation of jumping components and the results of the deduction
表2. 跳跃成分计算和扣除结果
Table 3. The frequency curve parameters of the series in recent and future condition
表3. 过去及现状未来条件下序列的频率曲线参数
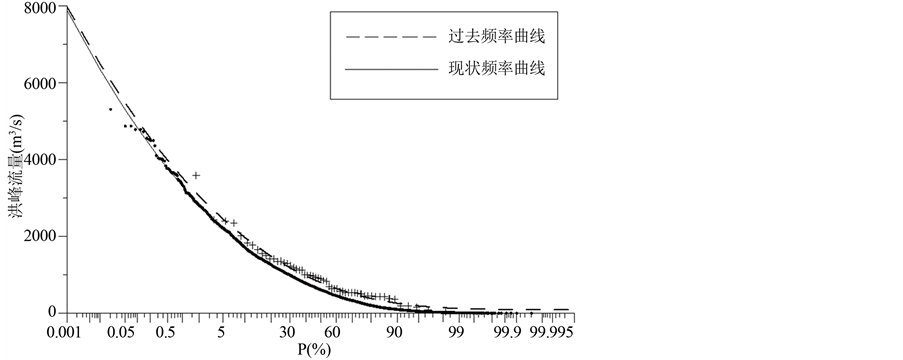
Figure 4. The frequency curve of the annual maximum flood peak series of Da Po Ling station in different periods
图4. 大坡岭站洪峰序列不同时期频率曲线图
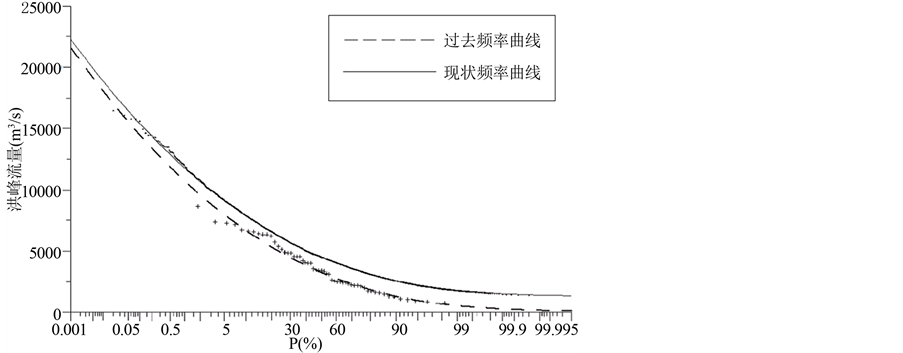
Figure 5. The frequency curve of the annual maximum flood peak series of Lu Tai Zi station in different periods
图5. 鲁台子站洪峰序列不同时期频率曲线图
台子站的洪峰序列则呈增加的态势，这与两个序列的跳跃变异情况相符合，为了将过去条件下与现状条件下的序列频率计算情况进行更详细的对比，下面将对比情况绘制表格。见表4，表5。
据表4、表5可以看出，两个序列的变化都相当大。大坡岭站的洪峰序列，在丰水年、平水年、枯水年的流量减少幅度为2.22%~18.51%、18.51%~19.48%、19.48%~97.27%。鲁台子站的洪峰序列，在丰水年、平水年、枯水年的流量增加幅度为4.43%~27.76%、27.76%~45.90%、45.90%~473.51%。可见，淮河流域的水文序列受到下垫面的影响比较剧烈，考虑变异求得的频率计算结果发生了很大差异。如果淮河流域要建设涉水工程时，需要使用设计洪水值。过去序列的设计洪水值已经不能满足实际情况，需要用现状和未来的频率曲线进行设计值的推求。这样才能更好地为各种涉水工程的设计、规划、施工提供依据，保证工程安全。
4. 结论
1) 本文利用线性回归检验法、斯皮尔曼秩次相关检验法、肯德尔秩次相关检验法对2个研究站点年最大洪峰值序列进行趋势性诊断，结果表明两个序列均未发生趋势变异。然后采用有序聚类法、最优信
表4. 大坡岭站洪峰序列不同时期的频率计算结果
Table 5. The frequency calculation results of the annual maximum flood peak series of Lu Tai Zi station in different periods
表5. 鲁台子站洪峰序列不同时期的频率计算结果
息二分法和滑动T值检验法对序列进行跳跃性诊断。结果显示，大坡岭站的年最大洪峰序列于1981年发生跳跃而鲁台子站的年最大洪峰序列在2001年发生了跳跃变异，且变异情况是具有物理成因基础的。
2) 假设非一致性水文序列由相对一致的随机性成分和非一致的确定性成分两部分组成。根据水文变异综合诊断的结果，对研究序列采用基于跳跃分析的非一致性年径流序列频率计算方法进行计算，得到了过去、现在和未来条件下满足P-Ⅲ型频率分布的统计参数。
通过对2个变异水文序列的统计参数以及频率曲线的分析可知，上游大坡岭站的洪峰流量序列在未来条件下存在一定程度的减少，在丰水年、平水年、枯水年的流量减少幅度分别为2.22%~18.51%、18.51%~ 19.48%、19.48%~97.27%。中游鲁台子站的洪峰流量序列在未来条件下存在一定程度的增加，在丰水年、平水年、枯水年的流量增加幅度分别为4.43%~27.76%、27.76%~45.90%、45.90%~473.51%。若在这种情形下，新建一项涉水工程还是以过去条件下的洪水设计值作为参考，就会存在很大的工程安全隐患，必须考虑水文变异的情况，用未来条件下的频率计算结果推算设计值，以保证工程安全。
由于非一致性序列水文频率计算的复杂性，本文只是采用淮河的水文资料加以识别和验证，提出的分析方法仍然需要进一步研究和在其他更多受变化环境影响剧烈的流域进行应用和验证。
基金项目
国家自然科学基金(No. 51279140)，国家“十二五”水专项淮河课题(No. 2014ZX07204-006)。
NOTES
作者简介：林洁(1990-)，女(汉)，江苏，武汉大学水文及水资源系，硕士研究生，主要从事水经济模型方面的研究。