1. 引言
在现代密码学前沿应用中，流密码的设计与分析占据重要的位置。RC4[1] 是一个应用广泛的流密码算法，从eSTREAM项目[2] (ECRYPT Stream Cipher Project)中选出的HC256[3] 显示出潜在应用价值。
在目前的应用环境中，对不同流密码算法生成的01序列进行NIST(National Institute of Standards and Technology)随机性测试[4] 在密码学、安全领域起着重要的作用。当前的NIST检测包直接提供针对选定序列的测量功能，如何利用该类模型和方法做系统推广，是复杂应用环境需要重视的一类问题。
本文致力于比较不同产生机制下生成的二维可视化特征分布，对流密码算法HC256和RC4生成的01序列进行区分，并对HC256和RC4内部结构相似这一特征进行进一步探究，为后续的分析提供参考。首先对流密码算法生成的01序列分段进行NIST随机性检测，然后对测得的PValue值进行频率分布统计得到Pi，最后对Pi进行模幂运算投影，生成可视化特征分布图。
1.1. 流密码算法
RC4是Ron Rivest为RSA公司在1987年设计的一种流密码[1] 。RC4算法以随机置换作为基础，是一个密钥长度可变，面向字节流的流密码。已被应用于多种数据传输和网络协议中。
HC-256[3] 是欧洲流密码计划(eSTREAM)征集到的面向软件实现的快速同步流密码。HC-256借鉴了RC4的思想，同时引入了面向字节的非线性函数来更新系统的内部状态[2] 。由于HC256的内部结构和RC4结构类似，本文选取这两种算法进行分析比较。
1.2. NIST随机数检测标准
序列的随机性测试一直是信息安全领域重要的研究方向。美国NIST SP800-22测试标准[4] 包括15种测试手段。有别于常用的对选定长度的随机序列进行NIST随机性检测，本文对密钥流分段进行NIST随机性检测以寻求随机序列段与段之间的内在联系与区别，关注于流密码算法在同一条件下生成的01序列内部分段之间的关联。
1.3. 聚类分析
聚类分析是数据挖掘的一项重要的方法。聚类问题实际上是将一组数据分成若干个组，在这些组之间寻找数据之间内在的联系[5] 。
随着流密码在信息安全领域的深入应用，对于流密码的分析方法也在不断发展。本文没有采用典型的流密码分析方法[6] ，尝试对生成的密钥流进行多元统计分析，对数据进行分组，为聚类分析提供前期分类图形，为探索流密码内部机制之间的联系与差异，以及对密码序列之间的区分提供参考。
1.4. 区分攻击
区分攻击是一种灵活有效的密码分析方法，其基本思想是通过观察某些输入与输出比特之间的关系来判别这些比特是来自真随机源还是来自密码[7] 。
区分攻击的关键是寻找适当的区分器，不同于已有的区分攻击算法，本文致力于分析不同流密码算法生成的比特流，利用输出的二维可视化特征分布图对HC256和RC4流密码算法生成的01序列进行区分。该方法从另一个角度为密码分析研究提供一定的参考。
2. 方法
2.1. 系统总体架构
该系统可分为4个子模块，如图1所示：
1) 密钥流生成：流密码算法 (如：HC256，RC4等) 生成1、0序列；
2) NIST随机性检测：用NIST方法(如：块内频数检验，频率检测，二元矩阵秩检验，离散傅立叶变换检验等)分段(4000 bit/组，1000 bit/组…)计算PValue值；
3) 频率分布直方图：对PValue值分组(25个/组，50个/组…)，画直方图(直方图区间数：2, 4, 8, 10, 16…)统计概率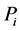
值；
4) 可视化：对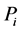
进行模幂运算或者对数运算 + 模幂运算，每张直方图得到一个二维坐标对
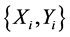，然后投影画图。
打点画图时X轴Y轴的坐标公式：(n：模幂运算的指数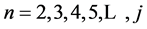
：概率分布直方图的区间数目
)
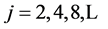模幂运算：
X轴：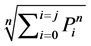
Y轴：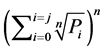
对数运算 + 模幂运算：
X轴：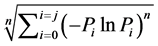
Y轴：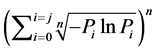
输入：
Key表示流密码算法生成01序列时，需要输入的初始密钥。
IV表示流密码算法生成01序列时，需要输入的初始向量。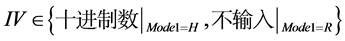
Mode1表示不同的流密码算法。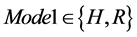
，Mode1 = H表示选用的算法是HC256，Mode1 = R表示选用的算法是RC4。
Figure 1. Architecture of the system
图1. 系统总体架构
LEN表示生成的01序列的长度，LEN > 0。
Mode2表示不同的NIST随机性检测算法。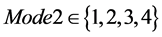
，Mode2 = 1表示选用的算法是块内频数检验，Mode2 = 2表示选用的算法是频率检测，Mode2 = 3表示选用的算法是二元矩阵秩检验，Mode2 = 4表示选用的算法是离散傅立叶变换检验。
r表示01序列的分段长度。
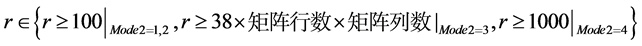
i表示统计频率分布直方图时，PValue序列的分段长度，i > 0。
j表示统计频率分布直方图时，直方图的区间数，j > 0。
Mode3表示不同的横纵坐标计算方法。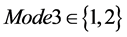
，Mode3 = 1表示选用的算法是模幂运算，Mode3 = 2表示选用的算法是对数运算 + 模幂运算。
n横纵坐标计算方法中模幂运算的指数，n > 0。
输出：
2D散点图二维可视化特征分布图。
2.2. 密钥流生成
见图2。
输入：
Mode1表示不同的流密码算法。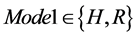
，Mode1 = H表示选用的算法是HC256，Mode1 = R表示选用的算法是RC4。
LEN表示生成的01序列的长度，LEN > 0。
Key表示流密码算法生成01序列时，需要输入的初始密钥。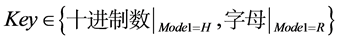
IV表示流密码算法生成01序列时，需要输入的初始向量。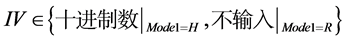
输出：
KeyStream 01序列。
2.3. NIST随机性检测
见图3。
输入：
KeyStream 01序列。
Mode2表示不同的NIST随机性检测算法。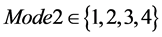
，Mode2 = 1表示选用的算法是块内频数检验，Mode2 = 2表示选用的算法是频率检测，Mode2 = 3表示选用的算法是二元矩阵秩检验，Mode2 = 4表示选用的算法是离散傅立叶变换检验。
r表示01序列的分段长度。
Figure 2. Architecture of key generation module
图2. 密钥流生成子模块
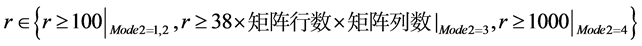
输出：
PValuePValue序列，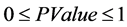
。
2.4. 频率分布直方图
见图4。
输入：
PValuePValue序列，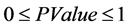
。
i表示统计频率分布直方图时，PValue序列的分段长度，i > 0。
j表示统计频率分布直方图时，直方图的区间数，j > 0。
输出：
Pi多组Pi值，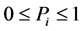
。
2.5. 可视化
见图5。
输入：
Pi多组Pi值，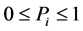
。
Mode3表示不同的横纵坐标计算方法。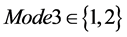
，Mod3 = 1表示选用的算法是模幂运算，Mode3
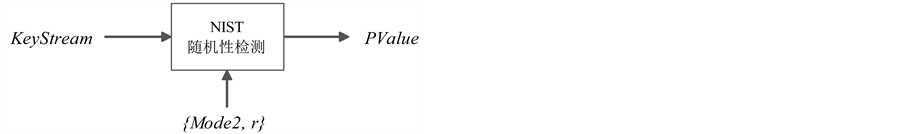
Figure 3. Architecture of NIST random number testing module
图3. NIST随机性检测子模块
Figure 4. Architecture of Frequency Distribution Histogram Module
图4. 频率分布直方图子模块
Figure 5. Architecture of visualization module
图5. 可视化子模块
= 2表示选用的算法是对数运算 + 模幂运算。
n横纵坐标计算方法中模幂运算的指数，n > 0。
输出：
2D散点图二维可视化特征分布图。
2.6. 各模块数据说明
从系统的架构来看，得到最终的2D散点图以前会生成三种中间数据，包括01序列、PValue序列、Pi序列，下面对这三种中间数据以及系统变量的取值进行说明。
2.6.1. 密钥流生成
为了使二维散点图的点数足够多，所以生成的01序列要足够长。本文01序列的长度(LEN)取值102,400,000，最终可得到10,240个点。为了便于比较分析，通过改变初始密钥Key和初始向量IV，获得不同的01序列。
2.6.2. NIST随机性检测
PValue值是NIST随机数检测方法输出的一个结果，每段01序列都可以得到一个PValue值，用来判定01序列是否是随机的。经过多次尝试，同一数据用四个不同的NIST随机数检测算法(Mode2)得到的散点图差异很小，所以最终结果展示以Mode2 = 1块内频数检验为例。当01序列的分段长度(r)取值400时，二维散点图分类比较明显。计算得到的PValue数据显示HC256，RC4生成的01序列具有良好的随机性。
2.6.3. 频率分布直方图
每段PValue序列做一个频率分布直方图，得到一组Pi值，全部PValue序列分段处理后得到多组Pi值。经过多次尝试，当PValue序列分段长度(i)取值25，直方图区间(j)取值10时，二维散点图分类比较明显。
2.6.4. 可视化
每组Pi值经过横纵坐标计算公式计算后得到一个二维坐标对，多组Pi值得到多组二维坐标对，根据得到的所有二维坐标值，确定二维散点图显示的横纵坐标范围，最终打点画图。同一数据用两个不同的横纵坐标计算方法 (Mode3)生成的图形大致对称，结果展示以Mode3 = 1模幂运算为例。当模幂运算指数(n)取值4时，二维散点图分类明显。
3. 结果
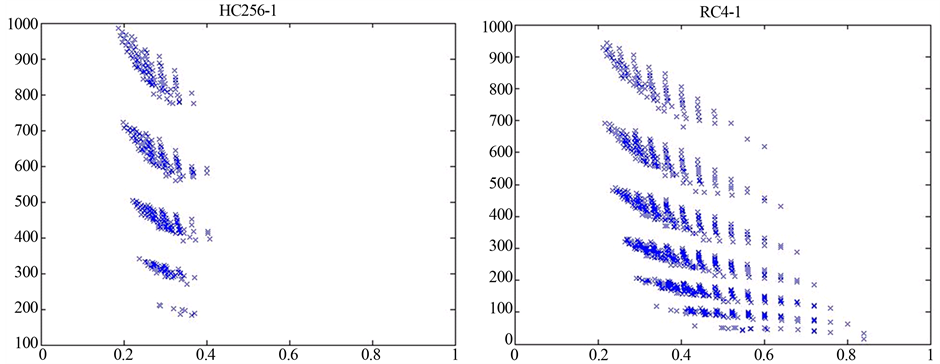
图6：LEN = 102,400,000，Mode2 = 1，r = 400，i = 25，j = 10，Mode3 = 1，n = 4。左边三个图形(a) (c) (e)展示的是HC256在不同初始密钥(Key)和初始向量(IV)下的二维散点图，右边三个图形(b) (d) (f)展示的是RC4在不同初始密钥(Key)下的二维散点图。通过改变初始密钥(Key)和初始向量(IV)值，可以比较相同流密码算法在不同初始密钥和初始向量下的异同，以及不同的流密码算法(Mode1)之间的异同。
图7：LEN = 102,400,000, r = 400, i = 25, j = 10, Mode3 = 2, n = 4。通过改变流密码算法(Mode1)和NIST随机数检测算法(Mode2)，比较不同流密码算法在不同NIST随机数检测算法下生成的二维可视化特征分布图的异同。
4. 讨论
由图6(a) (c) (e)和图(b) (d) (f)可看出，同一个流密码算法(Mode1)取不同的初始密钥(Key)和初始向量(IV)时，所得特征分布图相似度高，差别不大。
(a)(b)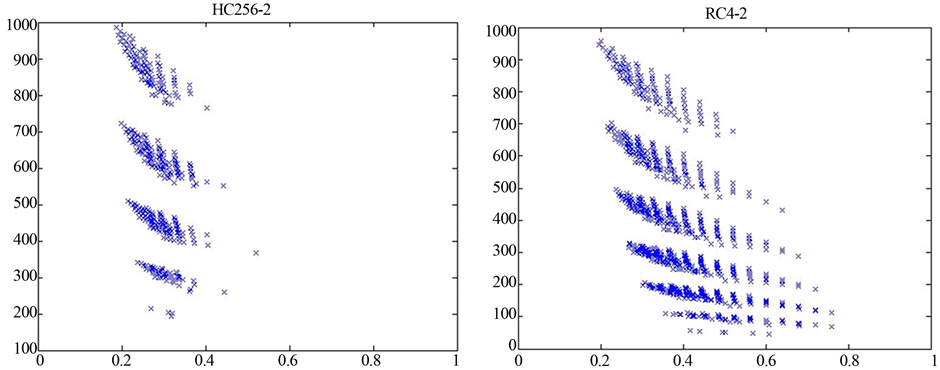 
(c)(d) 
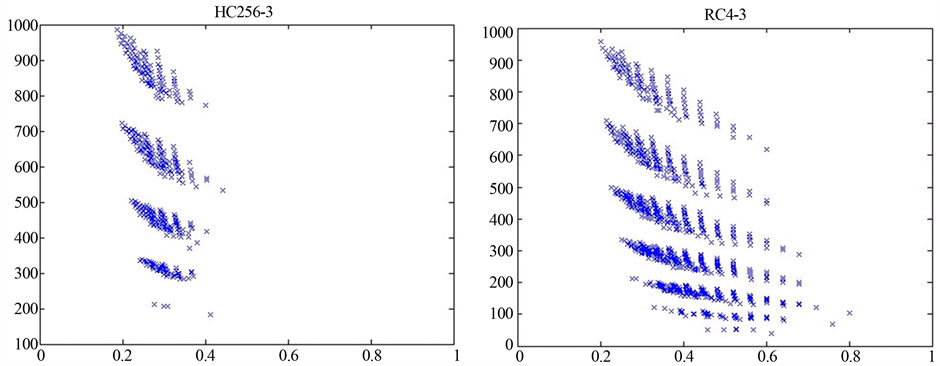(e)(f)
Figure 6. Six 2D scatter diagram in the range of LEN = 102,400,000, Mode2 = 1, r = 400, i = 25, j = 10, Mode3 = 1, n = 4
(a) Mode1 = H (10,240个点) Key: 00000000; IV: 00000000 (b) Mode1 = R (10,240个点) Key: lansry
(c) Mode1 = H (10,240个点) Key: 87654321; IV: 23456789 (d) Mode1 = R (10,240个点) Key: abcdefghijklmnopqrstuvwxyz
(e) Mode1 = H (10,240个点) Key: 73298906 IV: 75281900 (f) Mode1 = R (10,240个点) Key: qwertyuiopasdfghjklzxcvbnm
图6. 6张二维散点图：LEN = 102,400,000, Mode2 = 1, r = 400, i = 25, j = 10, Mode3 = 1, n = 4
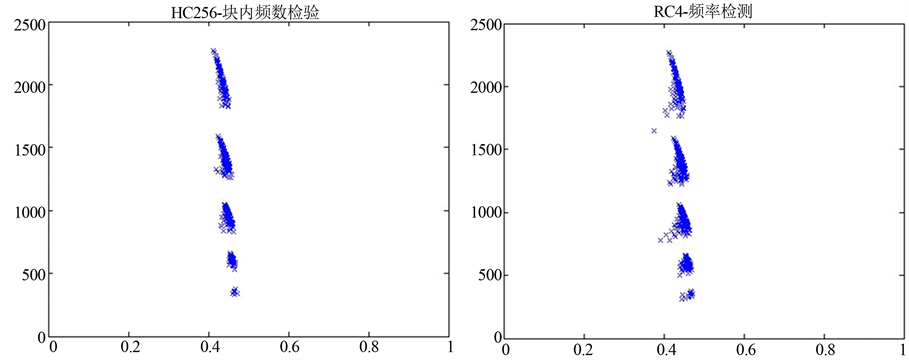
Figure 7. Two 2D scatter diagram in the range of LEN = 102,400,000, r = 400, i = 25, j = 10, Mode3 = 2, n = 4
(a) Mode1 = H, Mode2 = 1 (10,240个点) Key: 00000000, IV: 00000000 (b) Mode1 = R, Mode2 = 2 (10,240个点) Key: lansry
图7. 2张二维散点图：LEN = 102,400,000, r = 400, i = 25, j = 10, Mode3 = 2, n = 4
由图6(a) (c) (e)和图(b) (d) (f)对比可看出，不同的流密码算法的特征分布图不同，该系统可用来区分HC256和RC4生成的01序列，同时也表明了HC256和RC4都具有各自的特征图谱。
由图7可看出HC256的块内频数检验和RC4的频率检测所得图形类似，分析HC-256的内部结构可知，HC256有两个分别为1024个字的内部状态P和Q，每运行2048步这两个状态全部更新一次，两个状态互相影响，类似于RC4中SWAP函数。图7的两个特征分布图相似也许和HC256, RC4算法的内部机制相似有关。
5. 结论
通过本文的系统化测量可视化机制的处理，HC256和RC4这两种流密码算法生成的01序列显现出各自的特征图谱。通过该特征图谱可以对HC256和RC4生成的01序列进行区分，效果明显。同一流密码算法生成的不同01序列之间的特征图谱区分度不大，也进一步证明了HC256和RC4这两个流密码算法的安全性。
流密码在信息安全领域发挥的作用值得我们进一步对其进行探究。对NIST随机数测试方法做系统推广是复杂应用环境中需要重视的一类问题。对密钥流的随机性测量结果流进行多元统计分析形成可视化特征分布图作为流密码分析一个新的尝试，显示出巨大的潜力，具有一定的探索、研究价值。
项目基金
国家人才培养创新实验区资项目(RJ003)；国家自然科学基金项目(61362014)。
致 谢
感谢云南大学软件学院、云南省软件工程重点实验室信息安全基金及郑智捷博士国家自然科学基金 (61362014)的支持，感谢黄源霖提供的NIST随机数检测代码。
NOTES
*通讯作者。