1. 引言
DNA序列由四元符号{A、T、G、C}组成，从生物学角度理解，它是由四种碱基线性组合而成，并呈现出一定的互补原则；就计算机学科而言，核苷酸表示的译码信息与计算机中“0”“1”所代表的信息一样。因此，DNA序列从计算机的层次分析，可当作一串随机自然密码，其中隐藏着生物学的规律。针对DNA序列分析的模型和方法在现代基因组的各类应用中扮演着重要角色[1] ，利用可视化工具展现序列的已知与未知联系，对DNA计算[2] 和密码学领域的研究和应用提供辅助参考价值。
聚类是一种在数据挖掘中常用的方法，能对无监督数据根据其相似性进行划分并归为可区分的子类。利用聚类分析，通过对相似基因组表达模式的挖掘可以推测出未知基因组的结构和功能。目前用于基因聚类分析的常见方法有把属于同一类的个体间距离尽可能小，把不同类个体间距离尽可能大的分层聚类[3] 如K-means算法[4] 、还有对样本的概率密度分布进行估计的基于混合高斯模型的聚类算法[5] 等。通过利用相关的测量模型和方法，形成聚类分布能对后续使用聚类方法进行处理提供支持。
本文所描述的处理模型是对特定分组的基因片段，通过统计相同概率值在非线性函数作用下形成聚类分布的处理过程。该类方法基于概率值[6] ，将适用于随机序列的统计分析[7] 方法推广到基因序列中，对其进行整理归类，是一类具有应用价值的探索模式。
2. 系统体系构架
概率统计模型[8] 是解决复杂问题的有效方法。对于繁杂无序的DNA序列，可以认为，反映序列特征最重要的有两方面，其一是碱基的排列顺序，其二是碱基的含量。因此，考虑碱基在序列中所占比率也具有一定意义，根据分组概率值能进行可视化探索。
本文所构建的非线性函数DNA概率测量系统体系框架如图1所示。
系统处理包含概率值计算，非线性函数测量和可视化处理三个模块。概率值计算时需要进行四个操作，为递进关系。基于上述框架，处理流程可简述如图2所示。
输入的DNA序列依次进行分组、统计、分类、概率计算后，进入非线性函数处理的流程，最终将输出可视化的聚类分布图形。
3. 核心模块方法
3.1. 序列分组统计
选取DNA序列T，按照以下模式处理：(见图3)
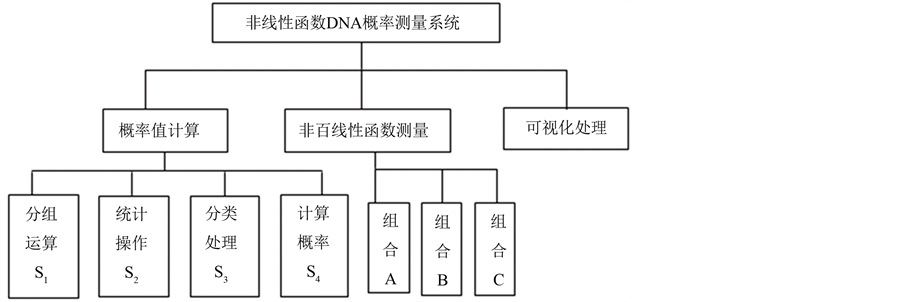
Figure 1. Nonlinear function of DNA probabilistic measurement system
图1. 非线性函数DNA概率测量系统框架图
Figure 2. Process flow diagram
图2. 处理流程简述图
Figure 3. DNA sequence grouping statistical methods
图3. DNA序列分组统计方法
输入组：
{M}表示序列T的个数集合，M∈N，N为正整数。
中间组：
S1运算盒表示将序列T进行一定数量Q1的分组。运算后，序列T的个数被分为n个序列Tn，其中0 ≤ Mn ≤ M，n = ⌊M/Q1⌋，Mn表示分组后一个序列的碱基个数，且M1 = M2 = … = Mn = Q1，多余或不足数据舍弃。
S2运算盒将S1得到的n个序列逐一统计相应碱基数目。
输出组：
经过S2处理后，对于每一个序列Tn，都将输出四个值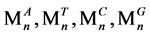
，
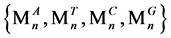表示此序列Tn中ATCG的个数。
至此序列一级分组的工作完成，有M个碱基的序列T经过上述操作后，被分为n组，得到的数据量为4n。
3.2. 序列分类统计
如图4所示。
输入组：
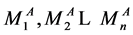为S2处理后每个序列Tn中碱基A的个数，总计n个，
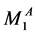与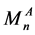
可能相同，也可能值不一样。
中间组：
S3运算盒表示将输入数据按照Q2个一组进行分类划分，得到j组，j = ⌊n/Q2⌋。为使最终可视化分别更具有表达性，Q2 > Q1。
输出组：
输出的j组数据中，每组有Q2个数据。
对于其他碱基，按照相同步骤处理。
3.3. 概率值P计算
如图5所示。
输入组：
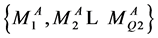为S3的第一组输出结果。
中间组：
S4运算盒的处理过程如下：
1) 将Q2个数据的值相加，得到总和sum；
2) 检索Q2个值，把相同值相加。例如有5个数据分别为32, 5, 40, 32, 21，处理后所得结果为64, 5, 40, 21；
3) 用步骤2中所得结果分别除以总和sum，得到其概率值为P1, P2 … PQ2，最多Q2个P值。
输出组：
输出概率P1, P2 … PQ2且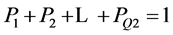
，0 ≤ Pn ≤ 1。
对于其他数据，按照相同步骤处理。
3.4. 非线性函数测量
设对概率值P处理的非线性函数为f1(P), f2(P)。f1(P)所计算的值作为横坐标X的值，f2(P)所计算的值作为相应纵坐标Y的值。这样对于每一个Pn值，可以在平面坐标系中得出一个点Wn(f1(Pn), f2(Pn))：(见图6)。
表1给出了本次所采用的非线性函数，对一个Pn值，采用三种不同的非线性函数计算：
sqrt(x)表示求x的平方根；pow(x, y)表示求x的y次方；exp(x)表示e的x次方。
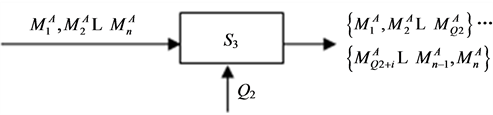
Figure 4. DNA sequence classification statistical methods
图4. DNA序列分类统计方法
Figure 5. DNA sequence probability P calculated methods
图5. DNA序列概率值P计算方法
Figure 6. Nonlinear function of the probability value processing methods
图6. 非线性函数对概率值的处理方法
Table 1. Nonlinear function evaluating expressions
表1. 非线性函数计算表达式
4. 测量结果
本次试验中，选取了基于RC4[9] 算法产生的伪随机数对应的DNA序列[10] 、动物鼠[11] 和植物水稻[12] 的部分碱基。
方便计算，定义总碱基数目M = 1,200,000，Q1 = 20，Q2 = 30，则n = M/Q1 = 60,000，j = n/Q2 = 2000。
为了将所得到的坐标形象化的显示出来，使用MATLAB[13] 绘制图像。统一坐标后，得到以下可视化的结果：
A. f1(P) = sqrt(P), f2(P) = pow(P, 4):
B. f1(P) = sqrt(P), f2(P) = exp(P):
C. f1(P) = pow(P, 4), f2(P) = exp(P):
5. 比较分析聚类结果
通过数据挖掘可视化的投影方法，绘制出了上文所示的各种聚类分布图，可获得不同的分布信息。
观察比较图7和图8，基于RC4算法产生的伪随机数对应的DNA序列与动植物所得到的可视化结果存在比较明显的差异。前者主要分布在1.6~2.4的区间，而对于鼠和水稻的显示看来，其开合度和聚散程度有着很大的相似度，集中体现在1.8~2.8。能看出，RC4碱基A、T与鼠和水稻的C、G分布相似，而RC4碱基C、G与鼠和水稻的A、T分布形态相同。图9并无明显的分层现象，碱基分布均呈现出束状。但同等条件下RC4开合度更大，鼠和水稻分布范围更广。
综合着不同算法相比较，碱基序列在同种非线性函数的测量下，所得到的图形走势大体相同。碱基A与T，C与G的延展性也整体一致，说明了它们互补的特性。此外，选取C函数测量时没有明显聚类效果，区间范围也不同，而A、B两种的分层效果明显，聚集范围一致。但B函数影响下的聚类分层可视化结果最为清晰。
6. 结束语
DNA序列的分析是现代分子生物学中最重要的部分[14] 。从生物数据库中的基本序出发，结合当前新兴的数据挖掘技术，分析基因数据，比较DNA 序列相似性，可以为生物信息、计算机安全学等方面提供一定的研究基础。
本文通过分析研究不同来源的DNA序列，在数据挖掘技术和可视化的基础上，设计了一种基于概率值和非线性函数操作的测量方法。运用该模型，在相同函数的影响下，可以得到趋势相同的分层效果图。由于文中仅针对部分的片段测量结果进行初步研究，存在不可避免的局限及不足。对应的不足之处希望在下一步的研究上继续完善。
致 谢
感谢国家自然科学基金、云南大学软件学院以及云南省软件工程重点实验室对信息安全研究项目的基金支持。
基金项目
国家自然科学基金资助项目(61362014)；云南大学软件学院2013年第四届教育创新基金资助项目(学生专项）