1. 引言
在1993年的ICC（国际通信会议）上，C. Berrou等人最先提出了Turbo码的概念[1] 。在Turbo码的设计思想中，将传统的卷积码与随机交织器十分巧妙的结合在了一起，既实现了随机编码，又完成了由短码构造长码的设计思想。同时，Turbo码还釆用了软输入软输出(SISO)的迭代译码方式来最大程度地逼近最大似然译码。由此，Turbo码得以获得了接近Shannon极限[2] 的良好性能。虽然至今Turbo码在数学上的机理还没有定论，但是它的优越的性能及迭代译码算法的思想已经被人们所理解。
Turbo码是一种非常复杂的信道编码方案，对Turbo码的具体实现还没有一个清楚的度量，因此需要使用计算机对系统进行仿真。目前的仿真大多基于编程的形式，是一种复杂和重复的方式，虽然有人采用Simulink进行仿真，但是对于交织、子译码等比较复杂的模块，仍需要重新编程，非常复杂。如何实现一种简单的仿真模型，以满足各种研究的需要，具有重要的现实意义，因此本文提出了一种基于Simulink的Turbo码仿真模型，该仿真模型完全基于Simulink的自有模块，无需自己编写模块程序，简化了编译器的复杂性。通过仿真，分析了迭代次数、交织长度、不同译码算法对Turbo码性能的影响。
2. Turbo码编译码原理
2.1. Turbo码编码
Turbo码的并行级联卷积码(PCCC)结构[3] 如图1所示，该结构主要由两个分量编码器RSC、交织器、复用与删余器组成。
Turbo码编码过程：输入信息序列复用为相同的三路，第一路直接送入复用与删余器，第二路送入分量编码器1，第三路送入交织器交织后再送入分量编码器2编码。两路编码器的输出以及第一路信号输入复用与删余器进行处理，构成码字序列输出。
分量编码器的最佳选择是递归系统卷积码(RSC)，输入信息经RSC输出码字具有较高的汉明距离，交织器的功能是置乱原数据的排列数据，降低码字之间的相关性。两者的结合是实现Turbo码近似随机编码的关键。复用与删余器作用是删除编码器输出校验序列中的部分校验位，以此提高编码速率，然后再与未编码的信息序列复用重组，由并转串最后输出。
2.2. Turbo码译码
Turbo码的基本译码结构[4] 如图2所示。
Turbo码编码译码器由两个软输入/软输出(SISO)译码器DEC1和DEC2串行级联而成，交织器与编码器中的所使用的交织器相同。译码器DEC1对分量码RSC1进行最佳译码。产生关于信息序列中每一
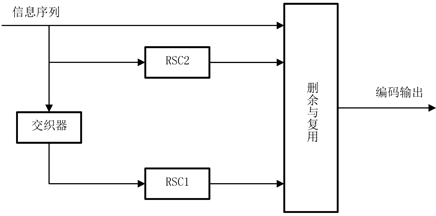
Figure 1. PCCC encoding structure
图1. PCCC编码结构
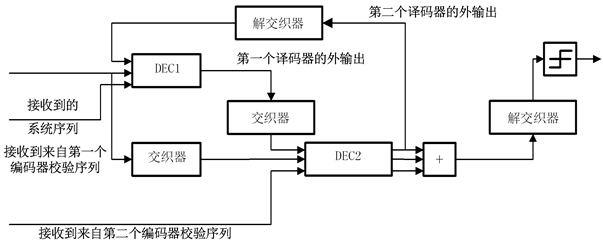
Figure 2. Decoding structure
图2. 译码结构
比特的似然信息，并将其中的“新信息”经过交织送给DEC2，译码器DEC2将此信息作为先验信息，对分量码RSC2进行最佳译码，产生关于交织后信息序列中每一比特的似然比信息，然后将其中的“外信息”经过解交织送给DEC1，进行下一次译码。这样，经过多次迭代，DEC1或DEC2的外输出信息趋于稳定，似然比值逼近于对整个码的最大似然译码，然后对此似然比进行硬判决，即可得到信息序列的最佳估计值。
3. Turbo码的仿真设计
3.1. Turbo码编码器设计
Turbo码编码器采用两个相同的分量编码器通过交织器级联而成。分量编码器是码率为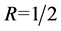
的RSC码，经过删余复用后总的Turbo码的码率
。
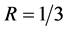序列产生用贝努利发生器(Bernoulli Binary Generator)。原始序列一路进入卷积编码器1(Convolutional Encoder1)，另一路经过随机交织器(Random Interleaver)后进入卷积编码器2(Convolutional Encoder2)。奇偶分离器1,2(Deinterlacer)将卷积编码器1,2的输出分别分成奇序列与偶序列。将卷积编码器1的奇序列、偶序列以及卷积编码器2的偶序列经复用器(Mux)合成一路串行序列，作为Turbo编码的输出。
卷积编码器的参数Trellis = poly2trellis(3,[7 5],7)，由于存在约束与反馈，奇偶分离器1输出的偶序列与原始序列相同。
3.2. Turbo码译码器设计
Simulink提供的APP Decode模块完成卷积码的后验概率译码。可以用该模块构建Turbo译码器。他有两个输入端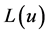
，
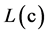和两个输出端
，
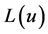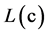。输入端
输入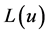原始序列的对数似然概率序列，输入端
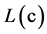输入编码器输出的对数似然概率序列。输出端
，
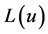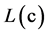是基于编码信息的更新序列的对数似然概率序列。
编码器输出序列经高斯白噪声信道(AWGN)加噪后送往译码器。该信号经解复用器(Demux)分成三路信号。第1、2路信号作为奇偶连接器(interlacer1）的奇偶输入，合成一路信号Out1。同理，第1路信号经随机交织器后与第3路信号输入奇偶连接器，合成一路信号Out2。
Turbo码译码器如图3所示，模块APP Decode1的输入端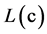
的输入In1为信号Out1，输入端
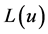的输入为上一次迭代后的结果，输出端
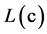终止，输出端
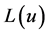经交织后作为模块APP Decode2的输入端
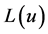的输入信号，Out2信号作为该模块的输入端
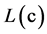输入信号In2。模块APP Decode2的输出端
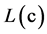终止，而输出端
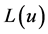经解交织后得到原始序列的对数似然比，经过延迟单元(Delay）延迟一个迭代周期，输出将作为下次迭代的输入，这样就完成了一次迭代。经多次迭代后得到的原始序列的对数似然比将越来越逼近于整个码的最大似然译码，再经硬判决后可以得到原始序列的最佳估计值。
完成本次仿真的关键是如何控制迭代的次数。假设每次迭代需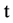
秒，则可以让贝努利发生器的每一帧的采样时间为
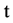秒，进行
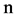次迭代需要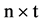
秒，通过零阶保持器(Zero Order Hold)将经过高斯白噪声信道的编码信号保持
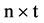秒，即可保证
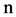次迭代。在第一次迭代时并没有上一次的迭代结果作为APP Decode1的输入端
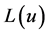的输入信号，为了避免这个错误，将迭代后信号与脉冲产生器(Discrete Pulse Generator)的输出信号相乘后作为APP Decode1输入端
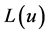的输入信号，脉冲产生器的参数设置为幅度为1，周期为
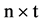秒，脉冲宽度为
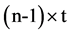，相位延迟为
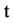秒，这样能保证第一次迭代时输入端有信号，信号为全0序列。
4. 仿真结果及分析
4.2. 迭代次数对Turbo码译码性能的影响
迭代译码结构是Turbo码具有良好的译码性能的重要原因。在交织长度为1024，采用译码算法为Max*时，选择迭代次数为3，7，9，对Turbo码性能影响进行比较。译码器性能如图4所示。
由图中可知，在相同的信噪比之下，迭代次数越多，误码率越低，译码性能越好。但是迭代系数为7,9时，译码性能差别甚微。这说明迭代次数为7时已经饱和[5] ，再增加迭代次数意义不大，反而增加不必要的计算负担。
4.2. 交织长度对Turbo码译码性能的影响
迭代次数为7，译码算法为Max*时，选取交织长度为51,210,242,048对Turbo码性能影响进行比较。
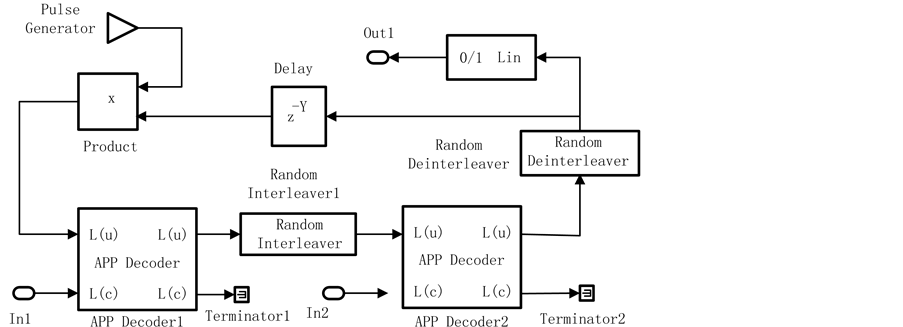
Figure 3. Decoder
图3. 译码器
由图5可知，随着信噪比的提高，Turbo码译码性能得到了显著的提高，而且交织长度越长，码译码性能越好。在实际的应用中，随着交织长度的增加，译码的复杂度，编码时延，传输时延，译码时延都会增加，所以需要根据具体的要求选定最佳的交织长度。
4.3. 译码算法对Turbo码译码性能的影响
APP译码器可以选择三种译码算法：True App、Max*、Max。图6是这三种算法的译码性能的比较，其中交织长度为1024，迭代次数为7次。比较而言，Max*算法与APP算法的译码性能相近，而且都优于MAX算法。
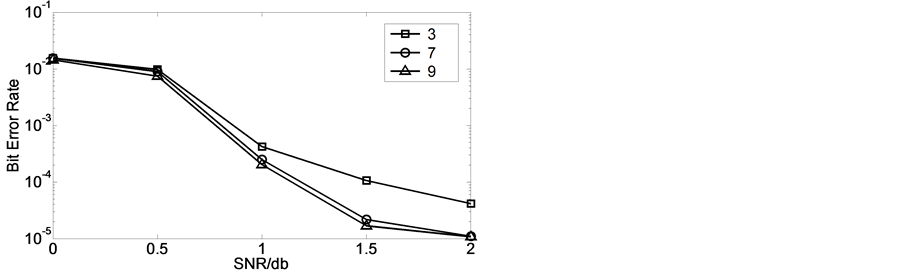
Figure 4. Decoding performance affected by iteration times
图4. 迭代次数对译码性能的影响
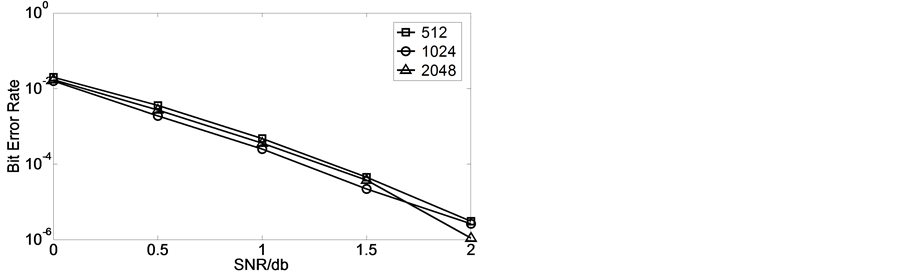
Figure 5. Decoding performance affected by interleaver length
图5. 交织长度对译码性能的影响
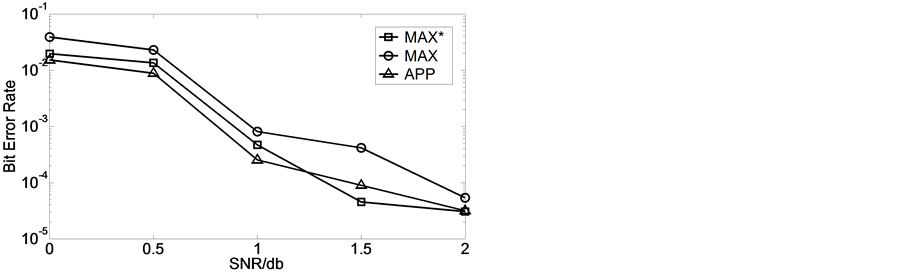
Figure 6. Decoding performance affected by decoding algorithm
图6. 译码算法对译码性能的影响
5. 结束语
提出了一种完全基于Simulink模块的Turbo码仿真模型，编码器采用并行级联卷积码结构，译码器由最大后验概率译码模块构成迭代结构，可以选择三种译码算法，方便了Turbo码的分析与研究。通过仿真结果，分析了迭代次数、交织长度、不同算法对译码性能影响，对实际的系统设计有一定的参考价值。
参考文献 (References）