1. 引言
在差分格式的构造以及差分格式的稳定性与收敛性的分析研究过程中,随着空间变量个数的增加,针对差分格式的数值求解也增加了新的困难。然而,差分格式的各种求解方法差别很大。例如我们在数值计算中经常碰到的,多个空间变量形式的隐格式的计算量明显大于显格式,这是由于我们在求解隐格式的过程中,每个时间层会多一个多维差分方程组需要给出确切的解。正是基于这个原因,我们可以巧妙地利用中间步将多维问题转化为若干个一维格式,进行分步求解,然后在每一步使用一个空间方向上的隐格式来计算,由此所设计的交替方向法不仅是无条件稳定的,而且可以用追赶法求解,基于以上优点交替分组方法是多变量问题求解的重要方法。这种方法的基础是Peaceman, Richford和Douglas所做的工作。例如1955年,Peaceman, Richford和Douglas同时提出求解二维抛物型方程的PR交替方向法,1962年Douglas和Richford将此格式上推广至三维,提出了稳定化校正格式等(见[1] )。这些格式的精度都是 ,本文主要构造了一种高精度交替方向格式,其截断误差达到
,本文主要构造了一种高精度交替方向格式,其截断误差达到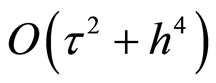 。
。
本文主要研究了一种交替分组显式方法(AGE)来求解Burgers方程。这一方法是由Evans和Abdullah(见[2] [3] )利用Saul’yev非对称格式构造而来,张宝琳等(见[4] [5] )推广到了对流扩散方程,并且进一步提出了交替分组显隐式方法,计算上更为精确,一定意义上扩大了原方法的应用范围。本文利用数值微分提出了一种新的交替分组显式格式,进一步推广了原方法,而且将其应用到Burgers方程,从结果看是可行的,精度也有了很大的提高。
2. Burgers方程高精度差分格式的构造
考虑Burgers方程:
 (1)
(1)
在区域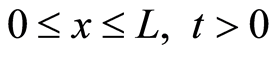 上,初边值条件为:
上,初边值条件为:
 (2)
(2)
 (3)
(3)
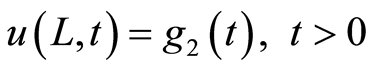 (4)
(4)
方程中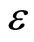 为已知常数,
为已知常数, 为已知函数。
为已知函数。
取时间步长为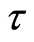 ,空间步长为
,空间步长为 (
( 为偶数),网格结点为
为偶数),网格结点为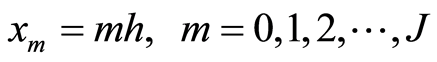 ;
;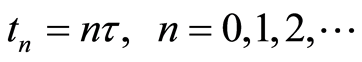
方程(1)在 处满足下列关系式:
处满足下列关系式:
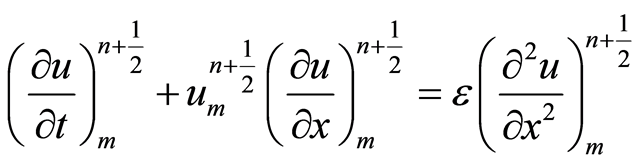 (5)
(5)
利用数值微分公式,有
 (6)
(6)
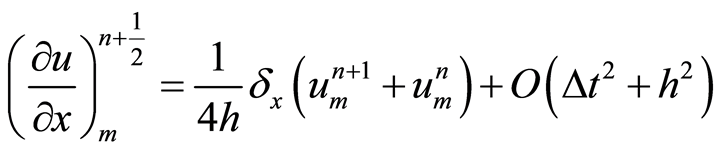 (7)
(7)
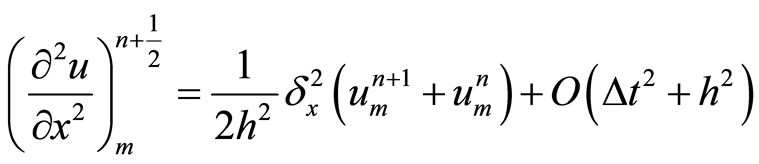 (8)
(8)
其中 和
和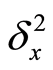 分别表示关于变量
分别表示关于变量 的一阶和二阶中心差分,代入式(5),舍去误差项得到差分方程
的一阶和二阶中心差分,代入式(5),舍去误差项得到差分方程
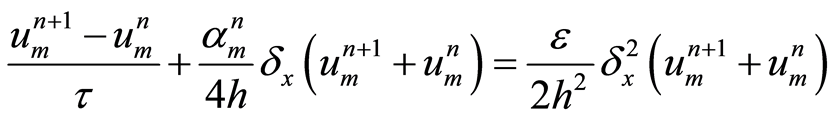 (9)
(9)
其中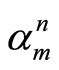 是
是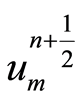 的某种近似。
的某种近似。
进一步可以得到(见[2] )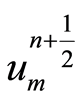 的近似值
的近似值 ,
,
 (10)
(10)
将式(10)代入式(9),经整理得到如下高精度隐格式(见[6] ):
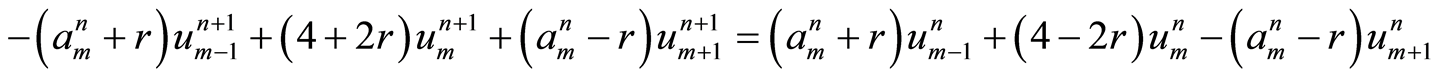 (11)
(11)
其中,
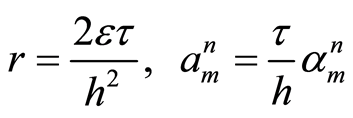 (12)
(12)
3. Burgers方程的交替分组差分法
为了得到Burgers方程的新的交替分组显式格式,在式(11)中令下标 ,得到差分方程组
,得到差分方程组
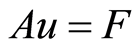 (13)
(13)
其中
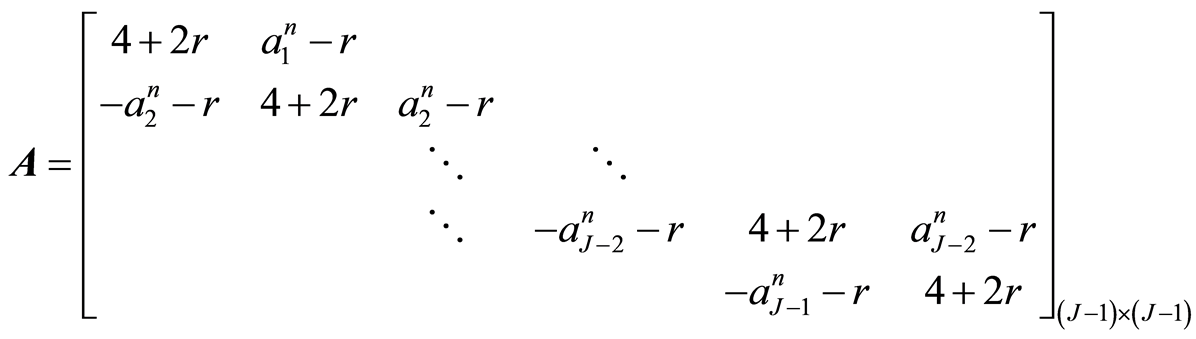


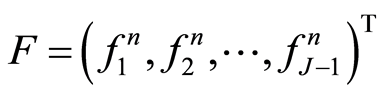




若令

其中
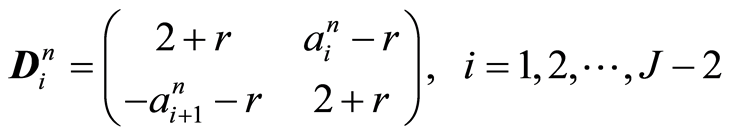
则系数矩阵A可分解为
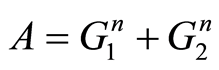 (14)
(14)
将式(14)代入式(13)得
 (15)
(15)
由此设计出交替分组显式迭代公式
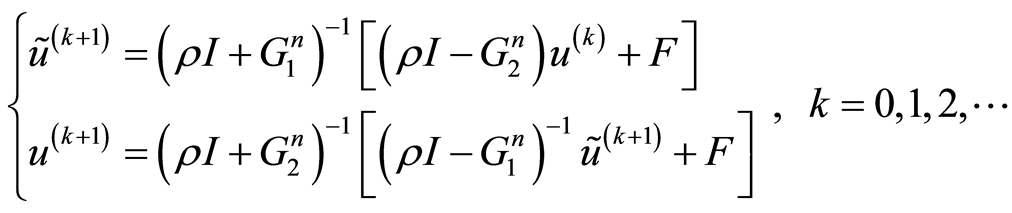 (16)
(16)
其中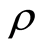 是使得
是使得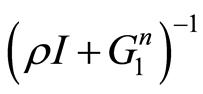 和
和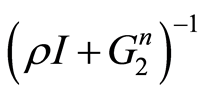 都存在的正数,在实际计算中可任意选取。且
都存在的正数,在实际计算中可任意选取。且
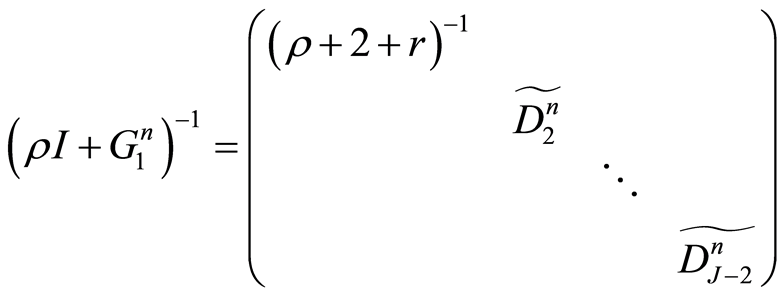

其中,
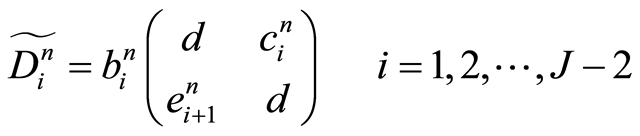


显然迭代公式(16)是完全显式的,并且非常适用于并行计算。
4. 稳定性与收敛性的线性化分析
首先利用线性化方法讨论差分格式(11)的稳定性。将式(1)中的对流速度取为常数 ,则格式(11)中的
,则格式(11)中的
 也是常数。根据Fourier分析方法,令
也是常数。根据Fourier分析方法,令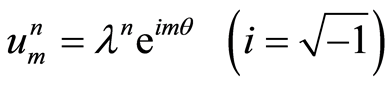 代入格式(11),经整理得到传播
代入格式(11),经整理得到传播
因子(见[7] )
 (17)
(17)
很明显,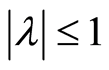 对于任意的
对于任意的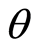 均成立,故格式(11)无条件稳定。
均成立,故格式(11)无条件稳定。
定理:当迭代矩阵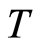 的谱半径
的谱半径 时,Burgers方程的交替分组差分格式(11)是收敛的。
时,Burgers方程的交替分组差分格式(11)是收敛的。
证明:从式(16)中消去 得:
得:
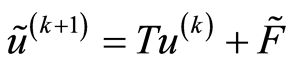 (18)
(18)
其中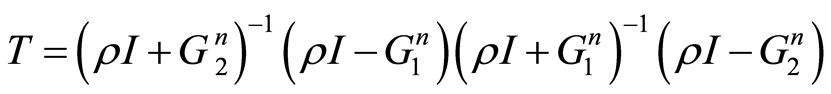 ,
, 。
。
定义矩阵
 (19)
(19)
有如下估计式
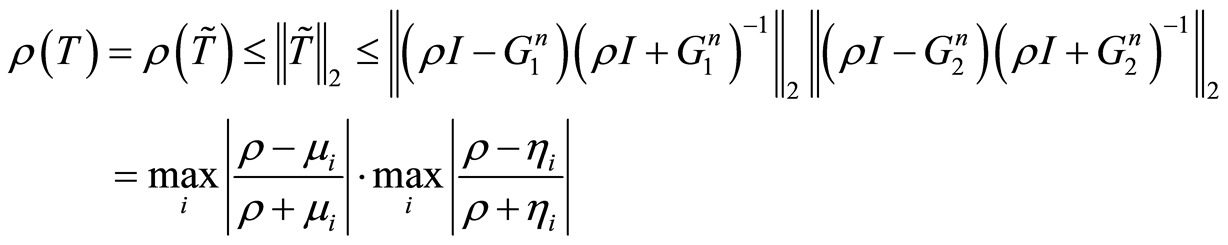 (20)
(20)
其中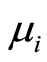 ,
,
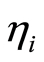 分别为
分别为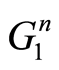 ,
,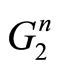 的特征值。当对流速度取常数
的特征值。当对流速度取常数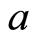 时,容易得到(见[8] )
时,容易得到(见[8] )
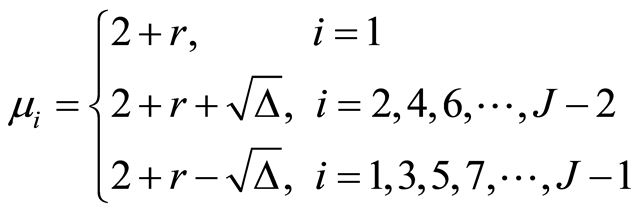 (21)
(21)
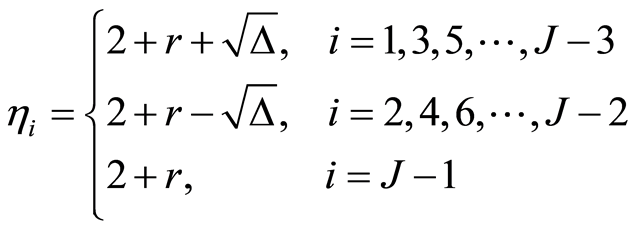 (22)
(22)
其中
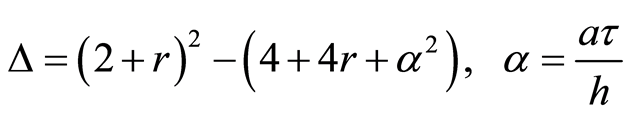 。
。
当 时,有
时,有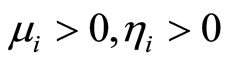 ,知
,知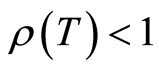 ;
;
当 时,有
时,有
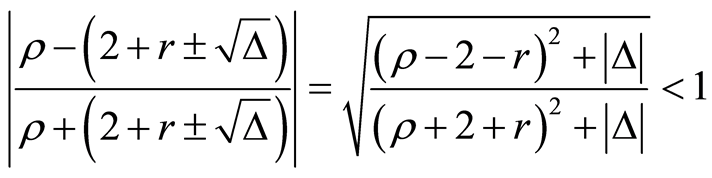 (23)
(23)
由此可见,无论 取何值,由式(20)知
取何值,由式(20)知 成立。
成立。
故迭代公式(11)是收敛的。
5. Burgers方程的交替分组差分法的数值算例
例1. 对于初边值问题:

在区域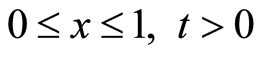 上的初边值条件为:
上的初边值条件为:
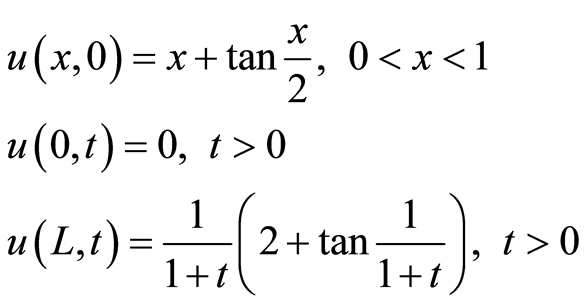
该问题有解析解(见[9] )
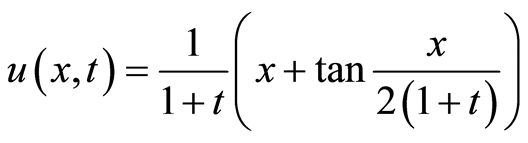 (24)
(24)
利用本研究提供的方法进行数值求解,取 ,表1给出了精确解与数值解的比较。
,表1给出了精确解与数值解的比较。
例2. 给定一Burgers方程:


Table 1. The comparison of exact and numerical solutions by two methods 
表1. 精确解和数值解的比较

Table 2. The comparison of exact and numerical solutions by two methods 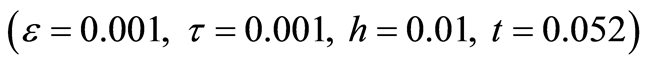
表2. 精确解和数值解的比较 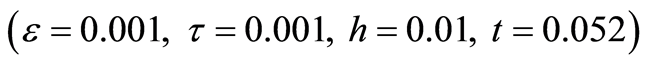
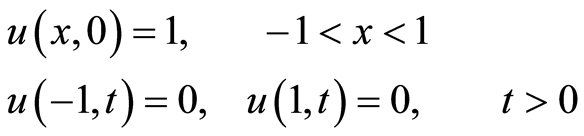
方程有如下的精确解:

其中

在此方程中取 ,
,
计算结果见表2。
由表1我们不难从数学直观上看出交替分组方法适用于Burgers方程,并且根据前文的讨论得知该方法是稳定的,绝对误差也是较小的。在例2中,我们研究了交替分组差分方法中关于 的数值选取对于计算结果的影响,从表2我们可以看到
的数值选取对于计算结果的影响,从表2我们可以看到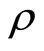 与0的关系直接影响了数值解与精确解之间的绝对误差。但是对于这种方法的最佳数值
与0的关系直接影响了数值解与精确解之间的绝对误差。但是对于这种方法的最佳数值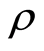 的选取,有待从理论上做进一步的讨论。
的选取,有待从理论上做进一步的讨论。
基金项目
青岛市科技计划基础研究项目(12-1-4-3-(2)-JCH)。

NOTES
*通讯作者。