基于故障字典与分支定界的模拟电路测试点优化方法

An Optimization Method for Test-Point of Analog Circuit Based on Fault Dictionary and the Branch and Bound

摘要: 为提高测试效率、降低测试代价，提出了一种基于故障字典与分支定界相结合的模拟电路测试点优化方法。以模糊集和故障字典为工具，以故障检测、故障隔离为约束，建立了测试点优化的0~1规划数学模型，并用分支定界法求解，最后用经典的测试优化电路对该方法进行仿真验证。仿真结果表明：上述方法在保证故障诊断需求的前提下实现了测试点快速优化，为实施测试提供了指导。

Abstract: To improve test efficiency and reduce test cost, an optimization method for test-point of analog circuit based on fault dictionary and the branch and bound is proposed. By the tool of fuzzy sets and fault dictionary, the 0-1 programming model for test-point optimization is established with the constraints of fault detection and fault isolation and the model is solved by the branch and bound method. Finally, the method is verified by simulating on the classic test optimization circuit. Simulation results show that the above method achieves a rapid optimization on the premise of ensuring the fault diagnosis needs and that it provides guidance for the test implementation.

1. 引言

当前，新型电子装备的功能电路80%以上由数字电路组成，模拟电路虽然只占很小的比例，但装备80%以上的故障由模拟电路产生，同时由于元器件容差的存在，模拟电路的测试诊断相对困难，因此，针对模拟系统开展测试诊断方法研究具有重要意义。

一个诊断系统的质量和效率取决于从系统中得到的故障信息[1] ，而故障信息来源于分布于系统上的测试点。相当一部分关于故障诊断的研究都默认测试点事先已经合理配置。实际中，受总体测试代价、可配置的测试资源等因素制约，不可能在所有测试

点上配置测试资源进行测试。通过对测试点优化，从中选取那些故障信息最大的测试点集，完全可以取得和对所有测试点都进行测试一样的故障分辨率。近来，确定一个具体诊断系统的测试点最优数目及其分布已引起人们关注[2] 。

2. 模糊集与故障字典概念

2.1. 模糊集的概念

测试点选择的原则是故障集中的故障均可隔离的前提下使得测试点数最少，因此，测试点选择过程也是故障隔离的过程。故障隔离意味着故障集中的故障能够被测试矢量区分，它通常有如式(1)判据[3] ：

(1)

其中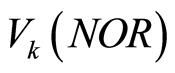，表示节点k的正常电压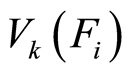，表示故障发生时节点k的电压，n是测试点数。由于元件参数容差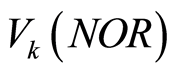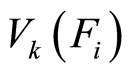，、都是一个区间而非一个点。故式(1)在实际中并不能直接应用。为解决这个问题，将每个测试矢量中的每个元素的值划分为若干个区域，每个区域的中心值为若干相邻元素值的平均值，然后从中心值左右扩展0.7 V，构成一个测试值区间，该区间称为一个模糊域。凡落在这个模糊域内的故障模式构成一个模糊集。不同模糊集可用模糊集号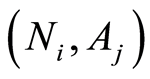来区分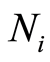，表示节点号，表示第j个模糊集，所有测试点所有的模糊集形成了模糊集表，该表反映了每一个测试点的模糊集划分状况，它一般通过电路仿真和模糊集划分得到[4] 。

2.2. 故障字典概念

在上文关于模糊集的相关论述中，为区分不同测试点对应的不同模糊集，定义了模糊集号，表示测试点对应的第j个模糊集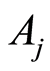，该模糊集内有若干个故障模式，这些故障模式落在同一个模糊域内。对于测试点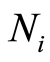，这样的模糊域有m个，将这m个不同模糊域的中心用数字分别编号，则同一个模糊集内的故障模式对应着相同的编号，这样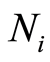所含模糊集中的故障模式都一一对应着某个数字编号。对于一定论域中的测试点集和故障集，按照上述方法，所有故障模式都通过数字编号的形式建立了与所有测试点之间的映射关系，这就是故障字典。一言以蔽之：故障字典就是行为测试点集、列为故障集、元素为对应的模糊域(模糊集)编号的矩阵，记为M。M的任一行称为故障编码。

3. 测试点优化模型与求解

本节以故障字典为工具，从故障隔离的约束出发，建立了测试点优化的整数规划数学模型并用分支定界法求解。

3.1. 基于故障字典的测试点优化问题建模

前已指明：测试点优选的要求是故障集F中的故障都能被隔离的前提下所需的测试点最少。故障都能被隔离意味着所有的故障对应着使得它们可区分的测试信息，对故障字典而言，就是要求故障集F中的任一故障对应着独一无二的故障编码，即所有故障编码两两互不相同。

首先来描述测试点优化问题中的两个基本要求：

1) 覆盖给定故障集F中的故障；

2) 隔离F中的故障。

第一个问题要求对任意f ∈ F，故障集F的故障特征向量至少有一个不全为零的列，即至少能有一个测试点能检测到该故障。第二个问题要求对任两个不同的故障f₁，f₂∈F，它们所对应的故障特征向量不同。基于假定特征向量，下面的定理把测试点优化问题归结为代数组合建模问题。

定理1[5] ：假设F代表系统故障集，T代表系统测试点集，M代表故障字典，那么故障检测和隔离问题归结为如下两点：

1) 当且仅当M中没有全为零的列时，T能检测给定故障集F中的所有故障；

2) 当且仅当M中的所有列均不同时，T能隔离给定故障集F中的所有故障。

显然，当且仅当M中的所有行均不同时，测试点集T能隔离给定故障集F中的所有故障。

基于上述论断，对测试点优化问题建模如下：选择M的最小列子集，使得由这些列子集新构成的子矩阵的行互不相同，则相应列子集对应的测试点即为最优测试点集。

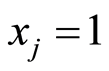下面通过公式进一步描述上述问题。考虑二进制向量，其维数与矩阵M列数相同，如果代表当且仅当选中M的第j列，那么X可以理解为是对M列子集的选择。设M行数为n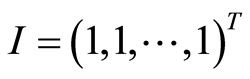，是有个元素全1向量，定义一个行、m列的矩阵A，A的每一行R_ij对应着M的两行R_i和R_j，定义，⊕表示异或运算，那么条件表示X所选择的解向量所构成的子矩阵没有相同的行。于是，测试点优化问题模型可表示为式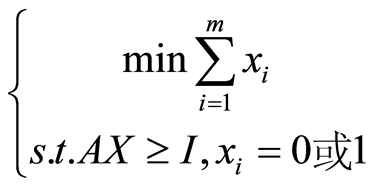(2)：

(2)

3.2. 基于分支定界法的模型求解

求解0~1整数规划问题常用方法有割平面法、分支定界法(Branch And Bound, BAB)等。其中BAB能保证全局最优并能避免穷尽搜索，它采用了类似分而治之的算法流程，不断将可行域分割成小的集合，然后在小的集合上找整数最优解。

为了说明BAB的一般原理，设有最小化整数规划问题P，相应的松弛问题P₀，如式(3)。

(3)

先求解P的松弛问题P₀。P₀的最优解不符合P的整数条件约束，取其中的非整数解分量x_i=a_i，在约束条件基础上增加一个整数约束条件或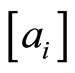，表示对a_i取整数，得到两个线性规划问题。BAB就是通过每次增加一个整数约束将P₀的可行域F分成两个子区域F₁、F₂，F₁、F₂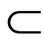F，称为分支。若子线性规划问题的解仍然不满足整数条件，则重复上述过程；若找到一个满足整数条件的解，则得到一个可行解，它的目标函数值就是一个界限，可作为衡量其他分支的一个依据，称为定界。用BAB求解式的算法流程如下：

Step 1：去掉变量的0~1要求，求出目标函数最小值，如所求解为整数解，计算停止，如果不是整数，则固定，转Step 2。

Step 2：以原问题或上一子问题为基础，分别增加两个约束，构成两个子问题：构成第一个子问题；，构成第二个子问题。

Step 3：分支原则：无效解不分支；整数解不分支；非整数解且其对应目标函数最小值大于已Step 1有整数Step 4解对应的目标函数最小值，不分支。除了上述三种情况都按Step 2分支。

当不能再分支后，比较所得的整数解，其中目标函数最小的，就是所要的最优解。

4. 实例验证

以图1中的滤波电路[6] 为实例，该电路的故障字典如表1所示。除了无故障状态，该故障字典M的维数为18 × 11，二进制向量，表示对M的列即测试点的选择，对M的所有行两两取异或得到约束矩阵A，其行为153、列为11，将上述条件代入并经过BAB求解可得，即最优化测试点集为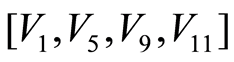，这与文献[6] 中的结论一致。

再以文献[6] 中的两级视频放大电路为实例，其故障字典参见文献。

该电路故障字典M的维数为16 × 13，二进制向量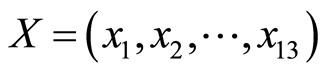，表示对M的列即测试点的选择，对M的所有行两两取异或得到约束矩阵A，其行为120、列为13，将上述条件代入并经过BAB求解可得，即最优化测试点集为，与文献[6] 中的结论一致。表2列出了本文方法与文献[6] 中的方法性能比较。

Figure 1. The schematic diagram of filter circuit

图1. 滤波电路原理图

Table 1. The fault dictionary of filter circuit

表1. 滤波电路故障字典

Table 2. Performance comparison of test-point optimization

表2. 测试点优选性能比较

5. 结论

以模糊集和故障字典为工具，从故障隔离的约束出发，建立了测试点优化的整数规划数学模型并用分支定界法求解，电路仿真应用表明：该方法在保证故障诊断需求的前提下实现了测试点快速优化。

基金项目

河北省重点基础研究(10963529D)资助项目；通用装备保障科研项目。