1. 引言
织物瑕疵是纺织产品生产中影响织物质量的重要因素之一，目前国内纺织工业织物瑕疵检测仍然采用人工方法来实现，瑕疵检测生产过程效率低，漏检率高，自动化程度低。在日夜生产中，不同光照给瑕疵检测带来分辨上的难度，且肉眼很难适应瞬间改变的光照。为解决这一难题引入机器视觉技术，通过计算机处理织布图像达到自动检测织物瑕疵的目的。
近几十年来，在织物瑕疵检测领域研究人员提出了许多不同的检测方法[1] [2] ，主要体现在不同的分割算法，主要有基于灰度共生矩阵的统计方法[3] [4] ，该方法通过提取图像的特征值进行图像分割，其特点简单明了，但容易受噪声和光照条件的干扰；基于傅里叶变换的检测算法[5] 在各工程实践中有着广泛的应用，其优点是速度快，但灵活性相对较差；基于Gabor滤波器的纹理分割算法[6] 和小波分解的纹理主频检测方法[7] 都是一种非常重要的时频分析方法，在时域和频域都有很好的局部性，但计算速度慢不适合在线监测；随着机器视觉技术的发展，研究人员又提出了一种基于聚类分析和支持向量机的分类方法[8] ，在检测织布瑕疵方面还不太成熟。这些领域虽取得了一定成果，但对外界因素干扰颇多的布匹生产实时监测还没形成一套合适的智能机制。
光照对织物颜色、清晰度和瑕疵形状有很大的影响。不同光照下的织布外观不同，但其结构却是唯一不变的。织物由经纬纱有规律的交织形成，具有一定的组织结构，织物表面由基本的组织结构周期性排列，所以织物纹理具有明显的周期性和方向性[9] 。然大多数织物疵点是由于织造过程中经纬纱不规则交织或缺少交织形成的，其纹理粗糙、不规则或缺失。且相对于颜色、形状等其他图像特征，纹理特征能够更好的兼顾图像宏观性质和细部结构两个方面[10] 。常用的纹理表达和描述方法主要有3种：统计法、结构法和频谱法[11] [12] 。
通过对上述几种方法的研究发现，傅里叶变换后的图像含有非常重要的空间频域信息和图像结构的方向性信息，图像的频谱特征对应图像的空间域[13] 。基于此，本文提出了一种基于傅里叶−极坐标变换的瑕疵检测方法，该方法通过分析极坐标中无瑕疵织布图像的傅里叶频谱，获得纹理主方向，滤去主方向的能量，经过反傅里叶变换得到的图像纹理会变模糊。在有瑕疵图像中，主方向纹理模糊后，瑕疵与正常纹理的对比度增强，这时进行边缘检测和二值化处理提取出瑕疵。该方法可以在不同的光照下很好地解决结构性瑕疵、破洞、跳线、油渍、经缩和纬缩等瑕疵，适应在线生产遇到的不同外界因素。
2. 基于傅里叶−极坐标检测方法
通过对预处理后的图像傅里叶变换，获得图像的频谱分布，傅里叶频谱中突出亮点的走向对应纹理模式的方向。设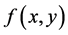
是一幅大小为
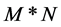的图像，二维傅里叶变换公式的定义为：
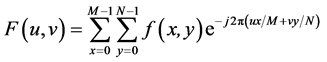(1)
式子中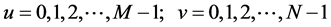
，
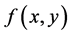代表图像矩阵中第
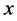行，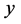
列的灰度像素值。如下一幅织布图1所示，经过傅里叶变换后，其频谱图像如图2，通过观察傅里叶变换后的频谱图可以看出图像的能量分布，频谱图像有很明显的方向性，且以图像中心为原点对称分布。极坐标变换对傅里叶频谱等分处理可以反映出图像纹理的结构方向性信息。
将频谱能量转化到二维极坐标上，使用极坐标来表示傅里叶频谱[11] ：
令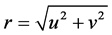
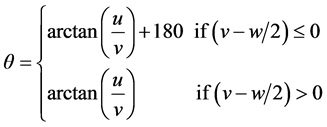(2)
式子中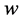
是宽度，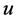
、
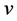是频域中的坐标，
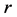代表极半径，
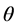代表与
方向所形成的角度。
由上式子得到一个函数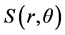
，其中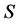
是频谱函数，
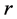和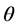
是该坐标系里的变量，对于每一个方向
，
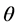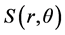可以视为一维函数
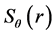；对每个确定的频率
，
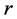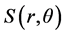是一维函数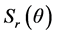
。因此对于给定的r，分析
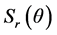可以得到频谱以原点为中心的圆上的行为特征。将此函数对下标求和，即可得到全局性的描述：
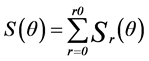(3)
式子中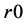
是频谱图像的最大半径，统计
角方向的能量和，比较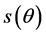
能量大小，找出最大能量所属角度，本文通过比较得出最大能量的方向角度是30˚，本文采用织布图的能量统计函数图(如图3)证明30˚是正确的方向，当
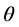等于30˚时可以看到频谱能量达到峰值，并且从频谱图上也可看到织布图像的频谱在30˚方向有连续5个亮点，上下分别有一条频谱线与
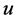方向夹角为30˚。由此认为数据的由来是正确的，该数据反映织布图像的纹理主方向是与
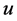方向夹角30o的方向。通过降低纹理主方向能量，增强瑕疵与纹理的对比度，其滤波器设计为如下(4)式：
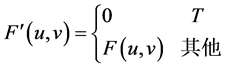(4)
T就是图4所示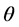的
角方向的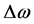
宽度的范围内的频谱能量，其中
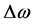选取20个像素的宽度。
将该范围内的能量置0，得到新的频域图像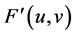
，通过傅里叶反变换重建图像
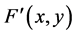，此时图像的纹理会被模糊甚至完全去除，瑕疵点就会凸显出来。
为了进一步增强瑕疵与纹理的对比度，本文采用Sobel边缘检测算子对图像进行增强，Sobel算子计算简单，不但能产生较好的边缘检测效果，而且受噪声影响也比较小，最后对图像进行二值化。该方法可以准确的将所有瑕疵点提取出来，效果显著。
3. 实验结果与结论
为了验证算法的准确性，其中开运算结构为2 × 2模板，去噪面积阈值为20，在实验中，选取不同规格的织布图，图像覆盖范围大小为512 × 512，在速度为30 m/min的布匹生产线进行50米内的瑕疵检测，人工统计瑕疵个数为64个，针对不同光照下的织布进行测试，测试结果如图5(c)，图6(c)，图7(c)，实验数据
Figure 1. Weave image
图1.织布图像
Figure 2. Spectrum image of FFT
图2. 傅里叶频谱图像
Figure 3. Energy distribute of weave image
图3. 织布图的能量分布
分析如表1。
图(a)为织布在不同光照下的原图，其中，图5(a)是在正常太阳光照下的瑕疵织物图像，图6(a)是夜晚白炽灯光照下的瑕疵织物图像，图7(a)是在阴雨天气的瑕疵织物图像。三幅图像在不同的光照下，颜色各不相同。图(b)是三幅不同光照下的织布瑕疵的增强图，经过傅里叶−极坐标变换滤去主方向纹理之后，进一步采用边缘检测增强瑕疵与纹理之间的对比度，由图可以看到瑕疵的形态。图5(b)在太阳光照下，光照不均匀会造成边缘检测时的乱象，由于瑕疵点的范围大，不影响瑕疵的提取。图6(b)白炽灯的照射下，光照比较均匀，瑕疵点的反射形成较鲜明的亮色，对瑕疵的提取有很大的优势。图7(b)为阴雨天气的瑕疵布匹，颜色呈现暗色瑕疵点不好辨认，但经过本文的傅里叶−极坐标变换，边缘检测图像很清
Table 1. Detection result of 50-m cloth defect under different illumination
表1. 不同光照下50米的织布瑕疵检测结果
(a)
(b)
(c)
Figure 5. Defective cloth under solar; (a) Defective cloth; (b) Enhancing defect; (c) Defective extraction
图5. 太阳光照下的瑕疵布匹；(a) 瑕疵布匹；(b) 瑕疵增强；(c)瑕疵提取
(a)
(b)
(c)
Figure 6. Defective cloth under filament lamp; (a) Defective cloth; (b) Enhancing defect; (c) Defective extraction
图6. 白炽灯下的瑕疵布匹；(a) 瑕疵布匹；(b) 瑕疵增强；(c)瑕疵提取
(a)
(b)
(c)
Figure 7. Defective cloth under rainy weather; (a) Defective cloth; (b) Enhancing defect; (c) Defective extraction
图7. 阴雨天气的瑕疵布匹；(a) 瑕疵布匹；(b) 瑕疵增强；(c)瑕疵提取
晰的将跳线瑕疵增强，图(c)为最后的瑕疵分割结果。经过二值化和填充的后期处理，三幅图像都定位瑕疵。图5(c)的瑕疵提取结果比原始图像的瑕疵点范围大，属于扩大瑕疵点，但对瑕疵的检测结果几乎没有影响，图6(c)的瑕疵检测的效果明显好于其他两个结果，不仅没有扩大瑕疵的范围，还准确的找到了右上角布匹的划痕。图7(c)的瑕疵检测显示了这是一系列的跳线瑕疵。跳线瑕疵太窄，往往会找不到或者在处理过程中丢失，但本文算法可以准确的检测出来。
从表1中，可以看到不同光照下，瑕疵检测成功率不是很一样，在阴雨天气下，瑕疵的检测成功率比其他两项低，究其原因是光照的暗淡降低了结构纹理的清晰度，但瑕疵的检测成功率都达到了90%以上，效果还是比较好的。本文仅针对牛仔布进行了详细的实验分析，但该方法仍可对棉麻布匹、针织织物等进行瑕疵检测，具有很好的检测效果，从而可以实现各种织物的瑕疵检测。
本文就织物在不同光照下进行检测实验，结果表明本文所给出的算法能将疵点准确的提取出来，具有良好的检测效果。实验数据分析结果和检测结果证明了该检测算法可以很好的实现在线监测瑕疵布匹。