1. 引言
汽车钢板弹簧是商用车非独立悬架的主要部件之一。它兼有悬架的弹性特性、导向特性和阻尼特性三大功能[1] ,另外其结构简单、制造与维修方便、成本低。依靠这些优点,钢板弹簧至今仍在商用车上得到广泛采用。
钢板弹簧约占汽车自重的5%~7%[2] ,随着人们对节约能源,节约材料要求的不断提高,致使汽车用钢板弹簧的轻量化需求不断加大。少片变截面钢板弹簧与相同功能的多片簧相比可节省钢材30%~50%[2] ,降低生产成本,节约油耗。其各片有大致相同的工作长度,其厚度沿片长按一定规律变化,叶片中应力趋于均匀分布,近似于等强度梁。同时由于簧片间加入了减摩垫片,使片间接触长度变短、动摩擦和动刚度减少,有利于提高整车的行驶平顺性。这就给变截面钢板弹簧带来了广阔的发展空间。
钢板弹簧传统的设计方法为:三角形板计算法、板端接触法、共同曲率法[3] [4] 。上述几种方法基于经验设计,设计中不免存在很多缺陷。尤其针对变截面板簧早期应力疲劳断裂问题,传统方法在设计过程中对材料及抛物线系数的选取并不能很好的解决这一问题。
某车型市场反馈报告显示,该车型使用的变截面板簧存在早期应力疲劳断裂问题。本文依据该车型板簧基本参数,基于有限元的CAE现代设计模式[3] [4] ,应用有限元分析软件ANSYS,按钢板弹簧实际的几何结构和材料属性,同时考虑其工作过程中的大变形、各片之间的接触等多种因素,对少片变截面钢板弹簧在自由装配状态下进行计算分析,取不同抛物线系数得到其在静负荷下的位移与应力等响应并作对比分析,较好地解决了变截面钢板弹簧设计存在的抛物线部分及根部骑马螺栓处易发生早期应力疲劳断裂问题[4] ,为实际钢板弹簧的设计与性能优化提供了依据。
2. 建立三维计算模型
首先根据变截面抛物线型钢板弹簧的基本参数在三维设计软件CATIA中建立其三维实体模型。在建立模型时,考虑到所选板簧的对称性和其工作长度,可取其工作长度的1/2模型以简化为悬臂梁结构作为仿真计算模型。计算中假定簧片处于伸直状态,弹簧变形满足小变形位移理论[5] ,不计变形时簧片之间的摩擦。为保证各簧片端部相接触,可在端部进行压弯处理以符合实际生产情况。然后导入分析软件ANSYS中。如图1所示为某车型的少片变截面抛物线型钢板弹簧的三维实体模型。
3. 静力分析设置
在ANSYS中,选择材质为Structural Steel,设置弹性模量为2.058 Gpa,泊松比为0.3。用基于六面体单元的Hex Dominant网格划分法对模型进行网格划分,该模型划分网格生成140,260个节点和31,516个单元。网格划分模型如图2所示。
少片变截面钢板弹簧总成在自由(非夹紧)状态下,其根部和端部接触,中间变截面部分存在间隙。基于少片簧片间摩擦影响较小,该模型定义对称不分离接触类型模拟根部和端部的片间接触。该接触类型假定接触对之间无间隙,不允许分离,但允许无摩擦滑动。
基于材料力学中悬臂梁理论[5] ,在板簧模型根部施加固定约束,限制其在X、Y和Z方向上的移动和绕各轴的转动。基于对称性,在板簧一片端部施加Y轴负方向的集中力10,780 N(静负荷的一半)。
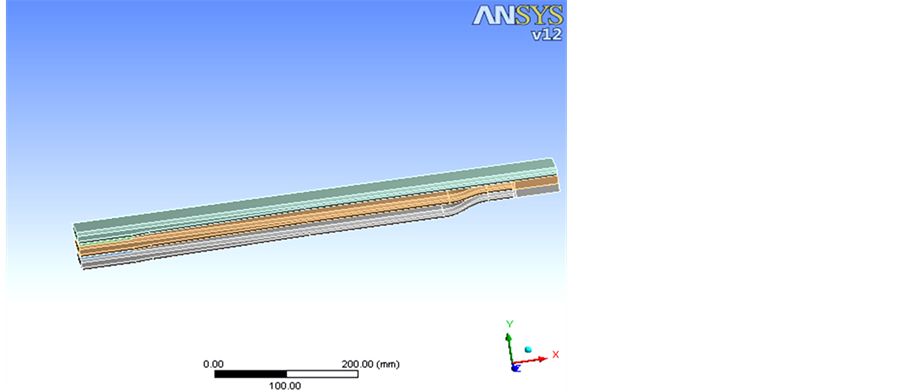
Figure 1. 3D model of the taper-leaf spring
图1. 钢板弹簧的三维模型图
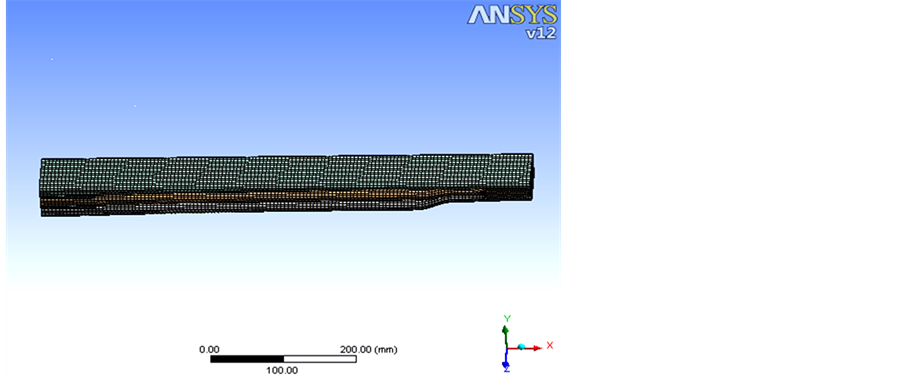
Figure 2. Grid model of the taper-leaf spring
图2. 钢板弹簧的网格模型图
4. 仿真结果分析
4.1. 原设计方案静力位移和应力分析
图3是用规格为18 × 75材料轧制成的3片变截面钢板弹簧总成在静负荷作用下Y轴方向上的位移图。图4是总成在静负荷作用下的米塞斯–应力图。
该方案变截面部分抛物线系数取0.69,其中加载处的位移为81.65 mm,该位移便是板簧总成在自由状态下的静挠度。从其米塞斯–应力图中可以看出,对于少片变截面板簧来说,其应力分布近似于等应力梁。变截面抛物线部分承受较大的等应力并且集中于簧片表面,根部骑马螺栓处的应力大小与抛物线处相比稍小,但应力也达到近600 Mpa。故该方案应力疲劳易发生在抛物线处和根部骑马螺栓处,易造成板簧早期损坏,降低寿命。
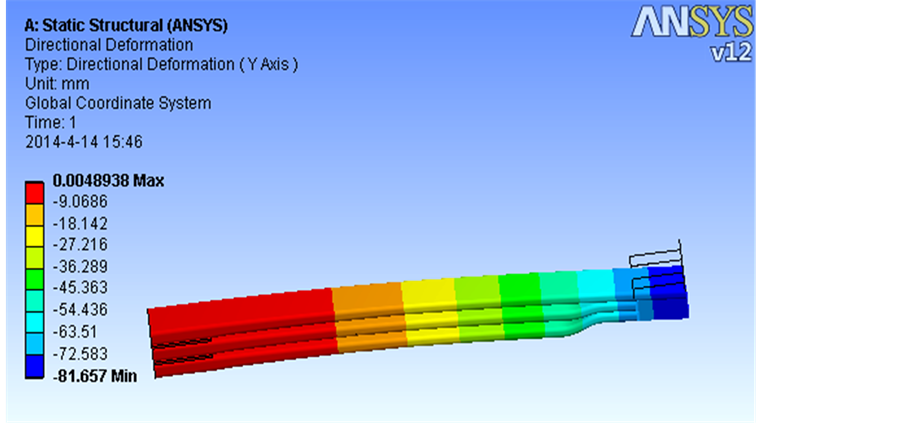
Figure 3. Y-axis displacement of the taper-leaf spring under full load
图3. 板簧总成在静负荷下Y轴方向上的位移图
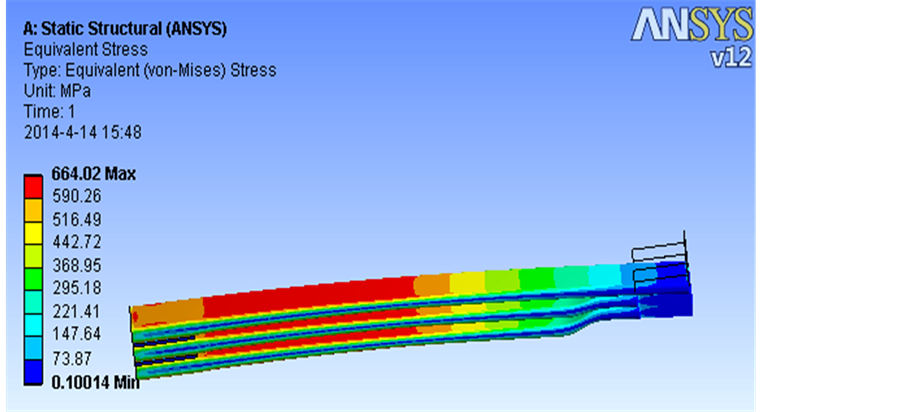
Figure 4. Von-Mises of the taper-leaf spring under full load
图4. 板簧总成在静负荷下的米塞斯应力图
4.2. 板簧优化设计对比分析
针对原设计方案中设计应力较大的问题,可考虑使用20 × 75材料增大根部的厚度,以增加根部的应力承受能力。同时,需增大抛物线系数以降低抛物线部分的应力。
4.2.1. 优化方案一仿真对比分析
该优化方案的抛物线系数取0.73。由位移图5可知,总成静挠度[6] 为76.8 mm,计算其仿真刚度为281 N/mm,稍高于理论刚度值276 N/mm,符合刚度要求。从应力图6可知,其等应力特性更明显,并且抛物线部分应力与原设计方案相比降低约60 Mpa,与理论应力相差约5%。根部骑马螺栓[6] 处应力与原设计方案相比亦降低约60 Mpa,而且根部厚度相应增加,这样根部应力承受能力得到明显提高。
4.2.2. 优化方案二仿真对比分析
考虑到变截面抛物线系数在优化方案一的基础上还有增大的空间,同时为充分利用材料取为0.76。
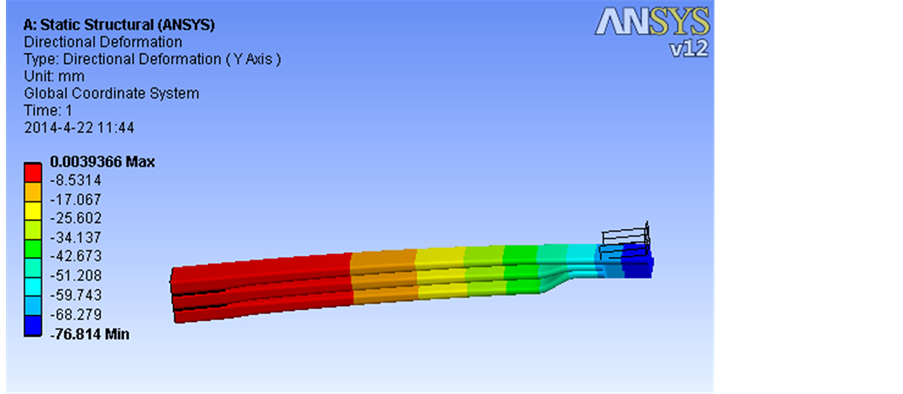
Figure 5. Y-axis displacement of the optimized plate spring under full load
图5. 优化板簧总成在静负荷下Y轴方向上的位移图
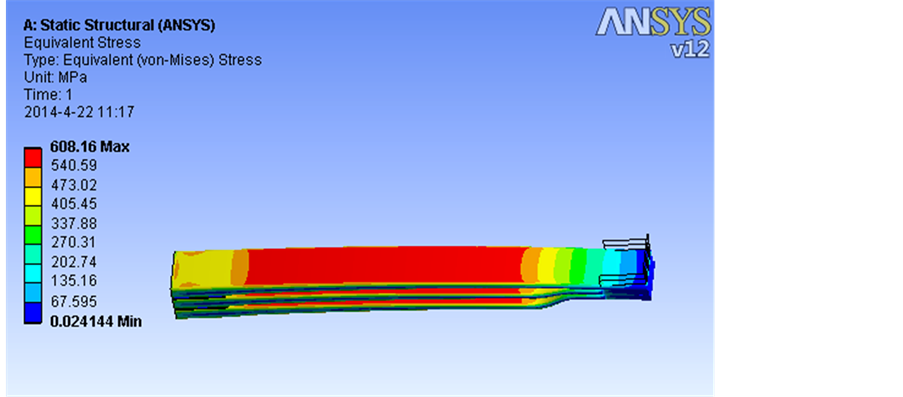
Figure 6. Von-Mises of the optimized plate spring under full load
图6. 优化板簧总成在静负荷下的米塞斯应力图
图7和图8分别是模型在静负荷下的位移图和应力图。由位移图7可计算得到其仿真刚度为306 N/mm,在其理论刚度偏差范围内(理论刚度299 N/mm)。由应力云图8的显示结果可知,其抛物线部分平均应力约为530 Mpa,根部骑马螺栓处平均应力约为470 Mpa。
表1为原设计方案与优化方案的理论和仿真性能参数表(数据结果参考附录中的理论公式)。由表1可知,板簧的刚度、静挠度和静载应力的仿真值符合其理论设计值。优化方案二与原设计方案相比,通过增加片厚和提高变截面抛物线系数,使其根部和抛物线部分应力在原设计方案的基础上降低了约100 Mpa,明显提高了这两处易发生应力疲劳区域的抗疲劳能力。在其刚度要求范围内和板簧总成重量只增重约2.5 kg的情况下,解决了变截面钢板弹簧设计存在的抛物线部分及根部骑马螺栓处易发生早期应力疲劳断裂的问题。并且由应力图可看出,优化方案二等应力特性明显改善,簧片大部分都承受相等的应力,这同样增强了簧片的抗疲劳能力。
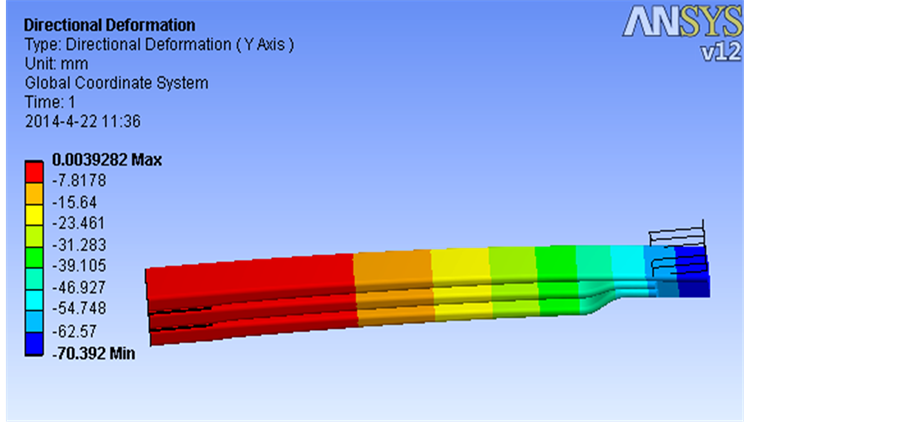
Figure 7. Y-axis displacement of the optimized plate spring under full load
图7. 优化板簧总成在静负荷下Y轴方向上的位移图
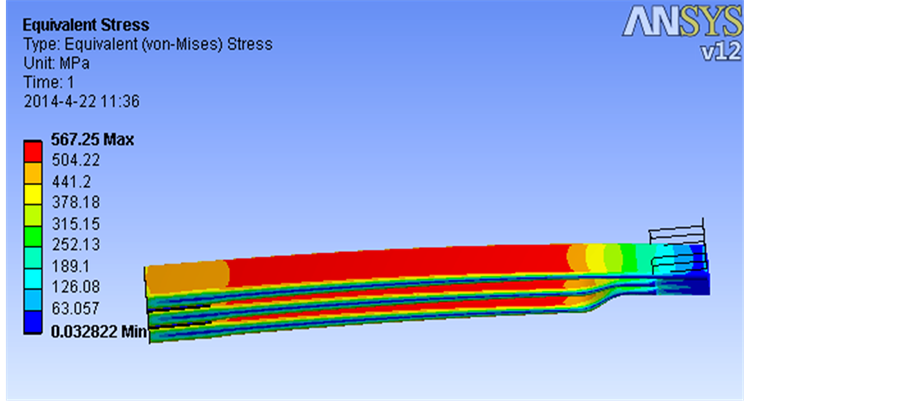
Figure 8. Von-Mises of the optimized plate spring under full load
图8. 优化板簧总成在静负荷下的米塞斯应力图

Table 1. Theory and simulation performance parameter table
表1. 理论与仿真性能参数表
两优化设计方案相比,方案二在方案一的基础上其抛物线系数增加了0.03,提高了材料利用率,使簧片所受的静载应力降低了约40 Mpa。由此可知,对于变截面钢板弹簧来说,其抛物线系数的取值对其受力影响效果明显,它的取值需满足所设计板簧的刚度和强度要求。
5. 结论
通过对不同抛物线系数的少片变截面钢板弹簧总成的有限元分析,计算得到其刚度和应力数据。经过对比分析,对变截面板簧其抛物线部分及根部骑马螺栓处易发生应力疲劳,是设计的薄弱环节。基于有限元的CAE分析技术可以较好的解决这一问题,为实际钢板弹簧的设计与性能优化提供了依据。所以应用有限元技术进行优化设计是今后板簧设计的有效指导方法之一。

附录
文中涉及的理论公式:
1) 刚度公式:
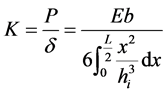
2) 根部应力公式:
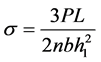
3) 抛物线处应力:
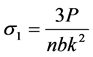
式中: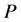 为负荷,
为负荷,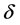 为挠度,
为挠度,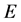 为弹性模量,
为弹性模量,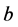 为簧片宽度,
为簧片宽度,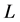 为工作长度,
为工作长度,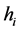 为簧片第i段厚度,
为簧片第i段厚度,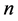 为簧片数,
为簧片数,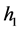 为簧片根部厚度,
为簧片根部厚度,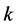 为抛物线系数。
为抛物线系数。