1. 引言
Schauder (参见文献[1] [2] )首先获得了一些二阶线性椭圆型方程解的先验估计。20世纪50年代,Schauder理论被推广到抛物型方程。由于Schauder的逐点估计在研究椭圆型与抛物型偏微分方程中的重要性,故命名Schauder所做的估计为Schauder估计。如今,Schauder估计在二阶线性椭圆型与抛物型偏微分方程的理论研究中起到了至关重要的作用,并且它已经被很多学者推广和简化。现在基本上有四种研究Schauder估计的方法。第一种方法是Schauder本人基于牛顿位势理论所用的方法。第二种方法由Campanato [3] 利用Campanato空间与Holder空间的等价性质来进行研究的方法。第三种方法由Trudinger [4] 构造磨光函数来研究解的Schauder 估计。第四种由Caffarelli [5] 应用扰动理论来得到二阶椭圆型方程黏性解的Schauder估计。抛物方程解的Schauder估计最早是由Ciliberto [6] 证明。事实上,在研究Schauder估计时,我们还可以使用一些新的方法(参见文献[7] -[12] )。最近,王在书[11] 系统地应用最大值原理方法,能量方法,紧方法等研究了椭圆型方程解的Schauder估计。本文我们将采用类似于紧方法的方法来研究下述热传导方程解的Schauder估计
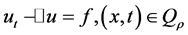 , (1)
, (1)
这里我们定义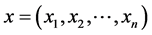 ,
,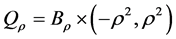 ,且
,且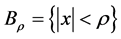 。
。
下面给出本文所要证明的主要结论。
定理1:设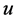 为方程(1)在
为方程(1)在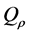 中的解,对任意的
中的解,对任意的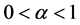 ,存在一个正常数
,存在一个正常数 ,使得当
,使得当 在
在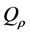 中的
中的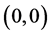 处是
处是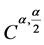 的,即
的,即
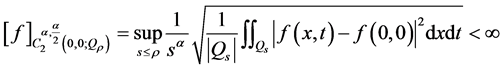 则
则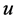 在
在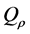 中的
中的 处是
处是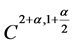 的,即存在一个二次多项式
的,即存在一个二次多项式
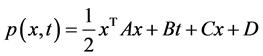
满足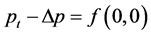 且对任意的
且对任意的 ,有
,有
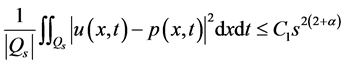 , (2)
, (2)
这里

且
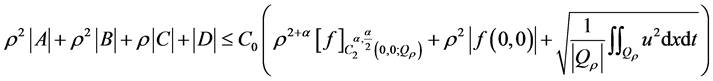 .
.
2. 主要结论的证明
引理1:设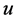 为方程(1)在
为方程(1)在 中的解,对任意的正数
中的解,对任意的正数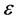 ,存在一个
,存在一个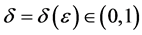 ,当
,当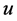 满足
满足
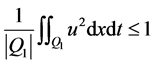 (3)
(3)
且
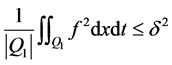 , (4)
, (4)
则存在一个函数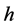 满足
满足 ,使得
,使得
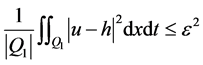 . (5)
. (5)
证明:取 满足
满足
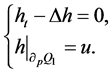
再令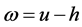 ,那么有
,那么有

由全局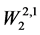 正则性估计,可得
正则性估计,可得
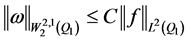 .
.
那么,由上式与(4)可得
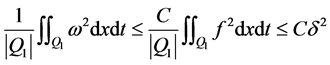 . (6)
. (6)
故
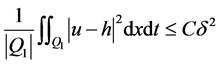 .
.
通过取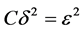 ,则
,则
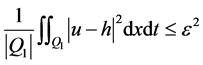 .
.
引理2:设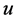 为方程(1)在
为方程(1)在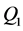 中的解,对任意的
中的解,对任意的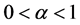 ,存在
,存在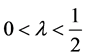 ,
, ,使得当
,使得当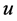 ,
,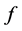 分别满足(3)与(4)时,那么存在一个二次多项式
分别满足(3)与(4)时,那么存在一个二次多项式
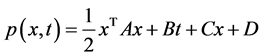 使得
使得 且
且
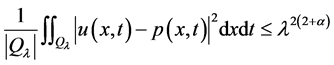 这里
这里
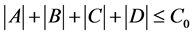 .
.
证明:由引理1可知,假设给定一个 ,则有
,则有
 , (7)
, (7)
这里 满足
满足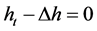 。故由(3)和(5)可得
。故由(3)和(5)可得
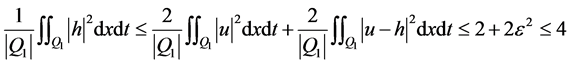 .
.
因此,由(文献[13] ,§2.3中定理9)与Holder不等式,可得
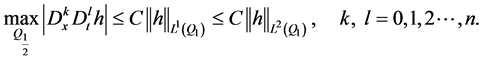
故由上面二式可得
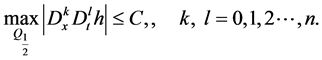 (8)
(8)
进一步,我们将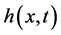 在
在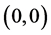 处Taylor展开后,取
处Taylor展开后,取
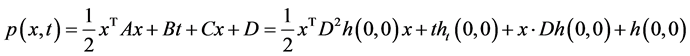 那么,
那么,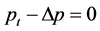 。再由中值定理与(8),我们可得,
。再由中值定理与(8),我们可得,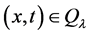 ,
,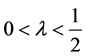 ,且
,且
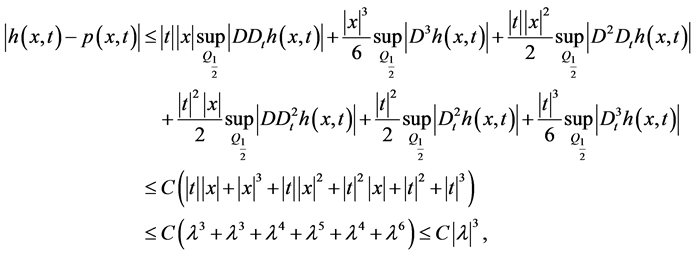 (9)
(9)
所以,由(7)和(9)可得
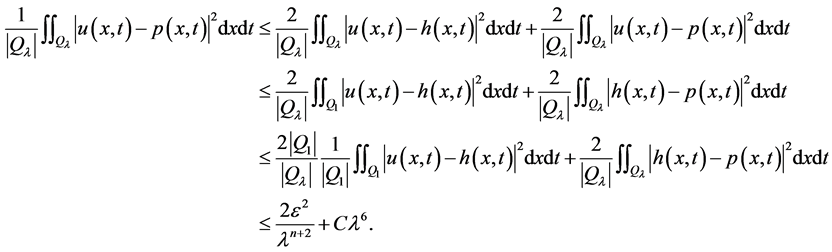 (10)
(10)
取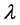 足够小,使得(10)中第二项满足
足够小,使得(10)中第二项满足
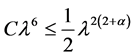 .
.
再取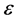 足够小,使得(10)中第一项满足
足够小,使得(10)中第一项满足
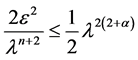 因此可得
因此可得
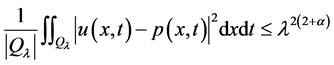 .
.
引理3:设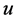 为方程(1)在
为方程(1)在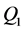 中的解,对任意的
中的解,对任意的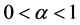 ,存在一个正常数
,存在一个正常数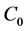 ,当
,当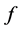 在
在 中是
中是 处
处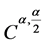 的,即
的,即
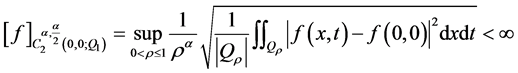 存在一个二次多项式
存在一个二次多项式
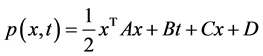
满足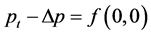 且
且
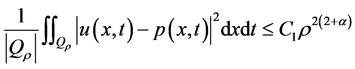 这里
这里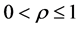 ,
,

且
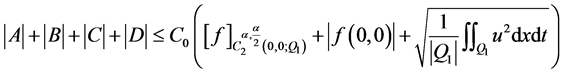 .
.
证明:我们不妨假设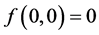 ,否则令
,否则令
 那么
那么
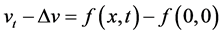 再把对
再把对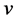 的估计转化到对
的估计转化到对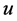 的估计即可。
的估计即可。
另外,我们可假设
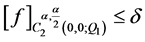 (11)
(11)
且
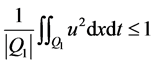 . (12)
. (12)
否则,可取
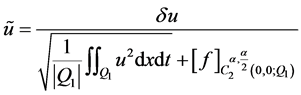 且
且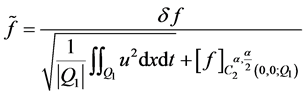 .
.
那么,易得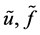 满足
满足
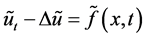 且
且 ,
, .
.
再把对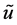 的估计转化到对
的估计转化到对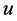 的估计即可。
的估计即可。
下面用归纳法证明:存在
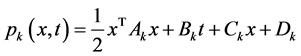 (13)
(13)
满足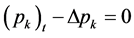 ,使得
,使得
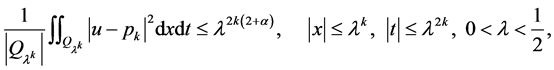 (14)
(14)
并且有
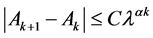 (15)
(15)
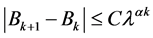 (16),
(16),
 (17)
(17)
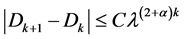 (18)
(18)
(i) 当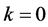 时。取
时。取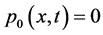 ,那么
,那么

显然成立。
(ii) 当 时。取
时。取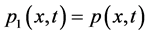 ,这里的
,这里的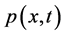 如引理2中所得。那么
如引理2中所得。那么
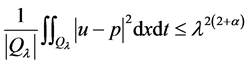
亦成立。
(iii) 假设 时成立。现在令
时成立。现在令
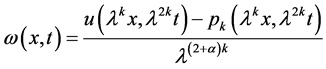 .
.
那么
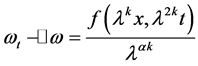 ,
, 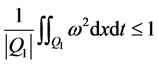 , 且
, 且 .
.
由引理2得:存在一个二次多项式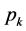 满足
满足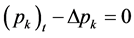 且
且
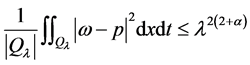
即
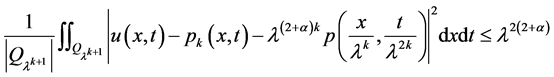 .
.
现取
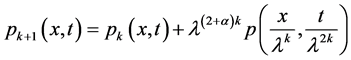 .
.
故易得对 情形也成立。进一步我们易得结论(13)~(18)成立.
情形也成立。进一步我们易得结论(13)~(18)成立.
下面证明当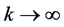 时,
时,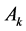 ,
, ,
,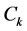 ,
,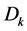 收敛于
收敛于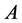 ,
, ,
,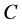 ,
,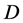 ,且有
,且有

满足
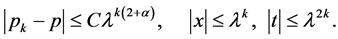 (19)
(19)
事实上,因为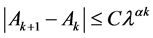 ,所以
,所以

由柯西收敛定理可知,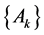 收敛,并且
收敛,并且 。
。
同理可得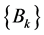 ,
,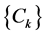 ,
,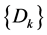 收敛,并且
收敛,并且
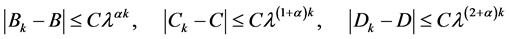 .
.
因此,对任意的 ,有
,有
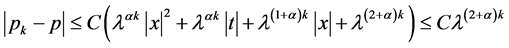 .
.
最后,对任意的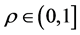 ,那么必存在某个
,那么必存在某个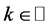 ,使得
,使得 。因此,利用(14)和(19)可得
。因此,利用(14)和(19)可得

故可得结论。
下面我们来证明本文的主要结论:定理1。
证明:令
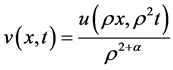 则
则
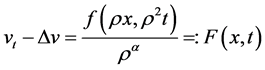 .
.
所以,由定理1的条件可得
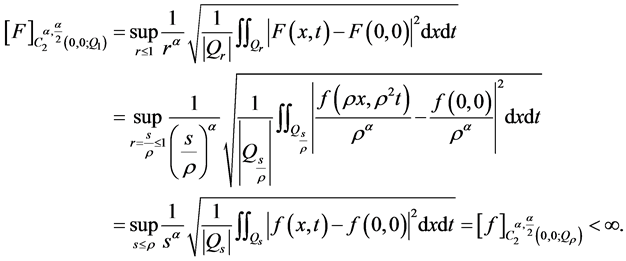
那么由引理3知:存在一个二次多项式

使得
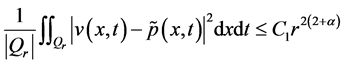 , (20)
, (20)
这里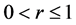 ,
,
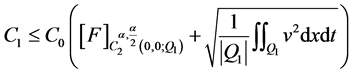 (21)
(21)
且
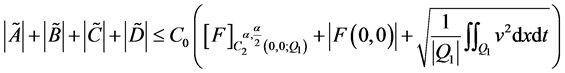 . (22)
. (22)
令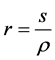 ,那么,由(20)可得
,那么,由(20)可得
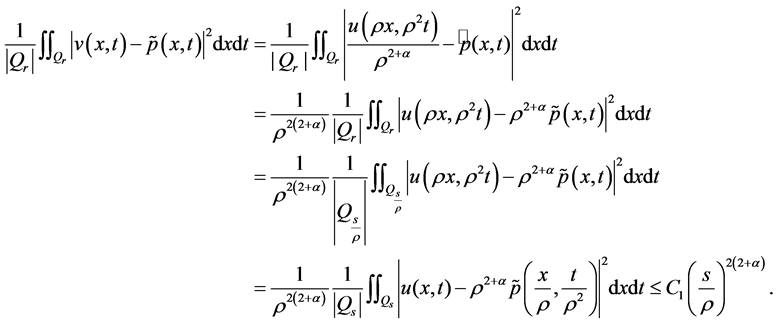
即
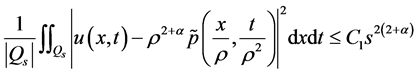 这里
这里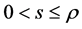 ,其中
,其中
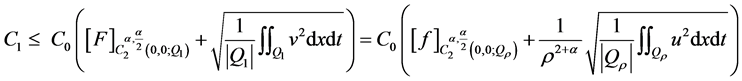 .
.
进一步取
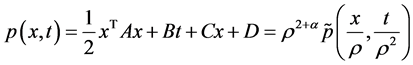 那么
那么
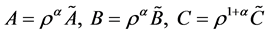 , 且
, 且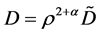 .
.
所以,由(22)可得
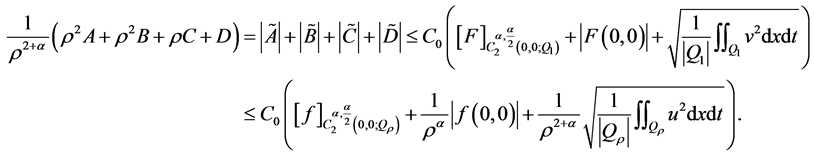
即
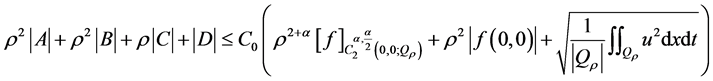 .
.
综上所述,结论得证。