1. 引言
由铁路货运部门承运的长大超重货物一般为国家经济建设的重点设备，超重货物对运输安全的影响主要表现在对运输设备的破坏，其中对桥梁的损坏是最突出的。由于种种原因，超重货物运输工作仍停留在手工计算的原始做法，甚至经常出现为确保运输安全而人为避开承载力足够的桥梁，严重浪费了运输能力，影响了铁路运输效益[1] -[8] 。因此，避开承载力不足的桥梁，找到合理的运输径路就显得极为迫切。
2. 最短路径问题的提出
如图1所示，在一个带权无向图中，从起点S到终点T，存在很多个中间节点。
如何选择所经过节点，使得路径最短就是一个典型的最短路径问题。所谓特定径路最短路径，在这里指的是满足用户约束条件的最短路径。
用户的约束条件是：给定起始节点(Start)与目标节点(Goal)以及该路径的必经节点序列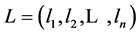
和避开节点序列
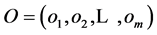。这里假设必经节点序列是顺序给出的，表示该路径的第
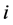个必经节点是
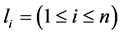；而避开节点序列中的节点没有顺序规定。产生的最短路径是由若干个节点组成的序列，即：
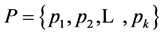，其中：
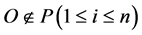
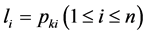
那么，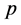
是一条满足上述条件的最短路径。
于是，网络图最短路问题的数学模型为：给定图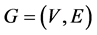
，
，
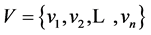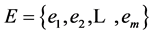。若图
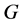的每条边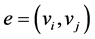
都与一个非负实数
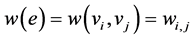对应，则称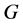
为非负赋权图，简称网络，其中
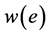称为e的权。
若p为
中v1至vn的路，称
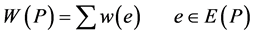
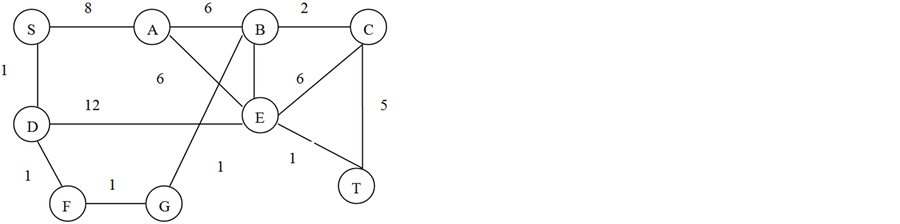
Figure 1. The shortest path problem raised
图1. 最短路问题的提出
为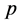
的长度，其中
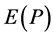表示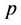
上边的集合。若
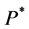为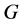
中v1至vn的路，且满足
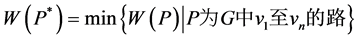
则称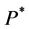
为v1至vn的最短路。
铁路两站间的距离绝对大于零，货运径路计算在具体应用中一般都是单源点问题，因此采用Dijkstra算法计算铁路站间最短路径是优选的方案。
3. 铁路网络结构的构建
3.1. 数据文件分析
如果计算节点之间的最短路径，那么在简化的路网上就可以进行，存储形式[9] 如表1所示。
如果计算站点中有非节点站，则调用站名文件，读出该非节点站至所在边两端节点站的距离，暂时删除这两节点站相连的边，添加一个节点以及两条边与断点相连，于是该节点站在路网中唯一，存储形式[9] 如表2所示。
添加障碍桥梁路段，即理论上“打断”承载力有限的桥梁，存储形式[9] 如表3所示。
3.2. 路网结构的拆分重构
通常利用铁路网的物理结构不能正确地计算货物运输的路径及里程，这正是一个难点[10] -[13] 。例如：从打柴沟至海石湾的货物运输路径，若利用物理网络结构求解最短路径，其最短径路必然是打柴沟–河口南–海石湾，如图2所示。
但对实际货物运输路径而言，正确的径路应该是打柴沟–河口南–兰州西–河口南–海石湾，该路径之所以要经河口南，东进兰州西，再西去河口南，原因是兰州西为接算站，河口南是支点站，如图3所示。
这样的车站在路网中不在少数。因此，在设计路网结构之前已将路网中的接算站部分在路网文件中进行了修改。
Table 1. The table of road network file
表1. 路网文件表
Table 2. The table of station name file
表2. 站名文件表
Table 3. The table of Bridge barriers file
表3. 障碍桥梁文件表
3.3. 解决站名重复的问题
在进行构架铁路网络时，为了解决铁路货物运输必经接算站的问题我们通过拆分重构物理路网结构的方法予以解决，然而这又引发了新的问题。如图3所示，图中出现了两个河口南。对于这种由于拆分重构而引起的站名重复问题，我们采用虚设源与汇的方法予以解决。如图4所示，对于图中产生的两个西固城，我们在网络中再加入一个西固城，这个新的西固城与之前的两个西固城有距离，且它们之间的距离为零。
当输入的发站站名是西固城这种情况时，我们就按照上述方法处理即可。当输入的到站站名重名时，处理方法同上。这样在求解最短路时就与真实距离一致了。
3.4. 添加非节点站
3.4.1. 添加中间站
当添加的站为中间站时，需找出该站在路网中的位置，即相邻节点站的序号，然后从站名文件中找出该站与相邻节点之间的记录，如图5所示，陇西站为中间站，查出该站在兰州西至天水之间，距兰州西213公里，距天水146公里，这样陇西站的位置就在路网中唯一指定了。
3.4.2. 添加支点站
当添加的站为支点站时，支点站一端为支线，一端与节点站相连，只需要找到相邻的支点站及与支
Figure 2. Physical structure of the road network
图2. 路网的物理结构
Figure 3. The logical structure of the road network
图3. 路网的逻辑结构
Figure 4. Dummy sources and sinks
图4. 虚设源与汇
点站的距离，就可以找到唯一的点与该支点站对应。如图6所示，刘家店为中间站，查出该站与陶来昭相连，距陶来昭35公里，这样刘家店站的位置就在路网中唯一指定了。
3.4.3. 发到站在同一区间
在实际运输过程中，可能会遇到发、到站在同一区间的情况，如果直接计算最短路，肯定会有迂回径路，这样既浪费设备又浪费时间，如图7所示。
利用中间站和节点站插入路网的方法导致定西和陇西这两个同一区段内不同中间站之间并不发生联系，定西到陇西的车流径路变成了定西–兰州西–陇西。如图7所示。
对于这种情况，就要分析是否到发两中间站或尽头站属于同一区段，若属于，则直接使这两个中间站或尽头站到同一节点站的距离相减取绝对值。解决了同一区段重复走行的问题，如图8所示，车流径路为：定西–陇西。
3.4.4. 添加障碍桥梁
在货物运输的过程中，会遇到一些设备上的能力不足问题，比如：桥梁承载能力问题，我们就需要避免经过这些路段，即将存在这些限制条件的路段理论上“打断”，寻找次短路。如图9所示。
3.5. 特定径路算法的实现
系统的结构框架大体可以分为路网结构的建立、是否能通过障碍桥梁和最短路径算法的求解。具体
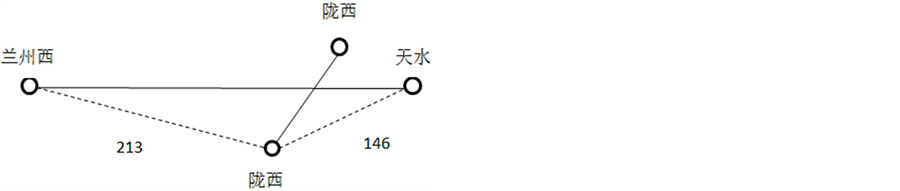
Figure 5. Adding intermediate stations in the network
图5. 在路网中添加中间站
Figure 6. Add fulcrum station in the network
图6. 在路网中添加支点站
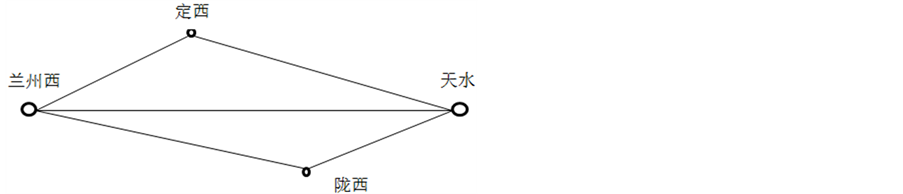
Figure 7. The situation of failure to handle the same interval
图7. 未按同一区间处理的情况
Figure 8. The situation of station in the same interval
图8. 发、到站在同一区间的情况
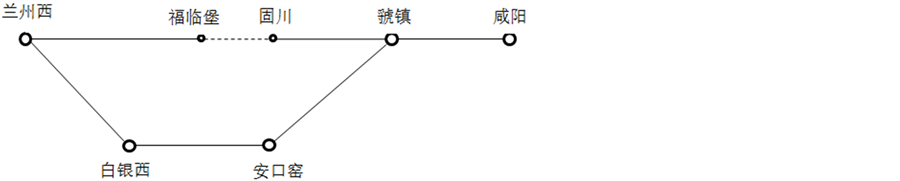
Figure 9. Add barriers bridges in the network
图9. 在路网中添加障碍桥梁
算法步骤如下：
第一步：将路网结构和桥梁基本资料的文件读入程序。
第二步：将桥梁的基本资料和路网中的具体障碍信息进行比较，看其是否能被承运。若能承运，则转第三步，否则，转第六步。
第三步：判断桥梁是否能通过。若不能通过，则转第四步，否则，转第五步。
第四步：读取路网障碍信息修改网络。
第五步：利用最短路径算法对建好的网络进行最短路径求解[14] 。
第六步：输出结果。
主程序算法流程如图10所示。
4. 测试结果
4.1. 在路网中两站最短路的实现
其结果如下所示：
发站：兰州西，到站：丰台西。车流重量330吨。兰州西和丰台西都是节点站。
运行程序如图11所示：
根据运行结果显示，该车流330吨，路网最短运输径路应该由兰州西、宝鸡，经西安西、介休到达丰台西，径路里程1798公里。由于路网中黄家寨至三桥段、福临堡至固川段、石家滩至拓石段、太谷至东观段有桥梁障碍。所以，程序在虚拟路网中将这4个区段切断，随后重新在路网中进行路径选择。求出的最短路径为兰州西、迎水桥，经阎良、郑州西到达丰台西，径路里程2222公里。
4.2. 结果分析
通过算例的计算，可以看出，当铁路部门承接集重货物的运输任务时，只要得知该货物的重量以及所用车种的自重，利用该程序则可以迅速、准确的给出该货物的具体运输路径。
4.3. 存在的不足
由于数据信息的缺乏，本程序计算出的最短路径不包括铁路特定运输路径的最短路，程序计算出的障碍信息都是根据现行铁路运输径路中障碍信息的一种模拟，如果铁路部门将真实路网中的具体障碍信息输入到路网数据文件中，那么利用该程序则可以迅速，准确的给出运输路径中的现实障碍情况，并实
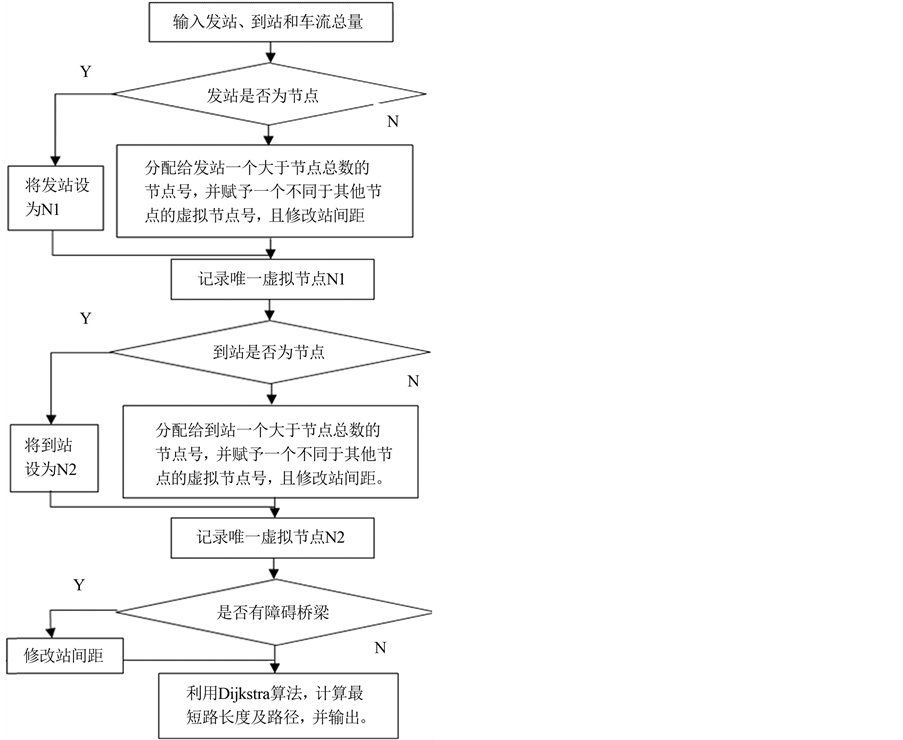
Figure 10. The flowchart of the main program algorithm
图10. 主程序算法流程图
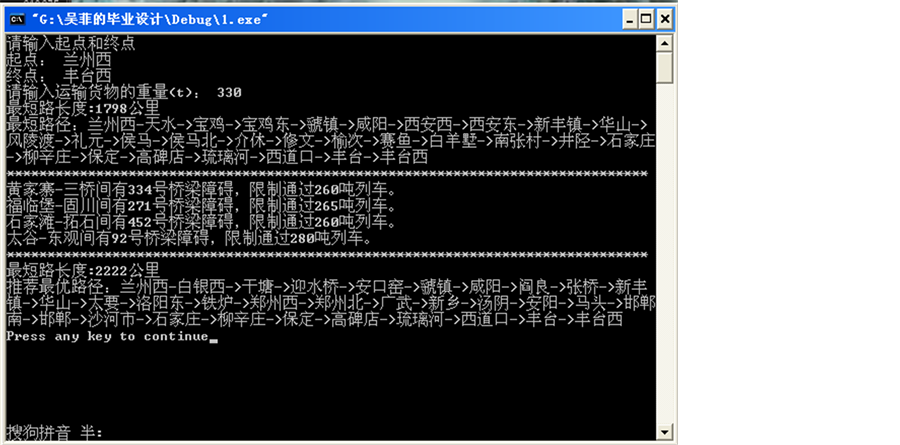
Figure 11. Achieve the shortest path between two stations in the road network
图11. 路网中两站间最短路的实现
现集重货物运输路径选择与现实一致。