1. 引言
正比计数管气体放大(俗称倍增)是带电粒子与管内气体分子发生非弹性电离碰撞产生雪崩的过程，雪崩产生的二次电子数与原初自由电子数成正比。对一个原初自由电子而言，它在其单位长度路径上产生的二次电子个数就称为第一汤森系数，在正比管倍增过程中起决定作用。正比管倍增与汤森系数及其管内电场的关系密切相关，但很难找到一个确定的解析函数来描述这种关系。为此人们基于特定气体和电场范围提出了三类不同的假设：线性关系[1] 、幂指数关系[2] 和自然指数关系[3] -[5] 。实验测量方面，自1997年Sernicki等[6] 测得有机蒸汽的第一汤森系数以来，二甲醚混合气体[7] 、Ar+异丁烷[8] 、C2H2F4-异丁烷[9] 、Ar + CO2[10] 、C2H2F4 + C4H10 + SF6[11] 、纯异丁烷[12] [13] 、氖[14] 、的汤森系数先后被测得。
理论与实验的结合始于Aoyama等人[15] 拟合Ar + 10% CH4和Xe + 5% CO2两种混合气体，并得出m = 12。而Kishimoto等人[16] 运用纯3He第一汤森电离系数得出充3He的正比计数管倍增因子是阳极丝直径的函数，且计算得出的倍增因子比温度为5 K时的实验值大很多。Sakurai等人[17] 研究了充以1 atm纯Xe气体和Xe + 5% CH4混合气体后的圆柱形正比计数管，得出了阳极丝直径与约化电场之间的关系。后来Uozumi等人[18] 与Mazed等人[19] [20] 提出了各自的关于第一汤森系数的半微观关系，并以Ar + CH4和Ar + CO2等混合气体为例，实验验证了该关系得出的气体倍增因子计算结果与实验数据符合较好。2004年Andronic等[21] 给出了基于Penning机制定量确定汤森系数的方法。
本文在综述前人成果的基础上，首先提出了约化汤森系数、约化倍增因子、临界约化场强、临界约化汤森系数的概念，并得出了相应约化汤森系数与约化电场关系的倍增因子表达式。以P10气体充入特定尺寸涂硼正比计数管为例，给出了三类关系及其对应约化倍增因子变化曲线图。通过对所得曲线图的分析，较深入地剖析了各种约化汤森系数及约化倍增因子随约化电场的变化关系的内在联系，论证了他们之间的一致性，最后得出了约化倍增因子随约化汤森系数假设变化的规律。
2. 约化汤森系数与约化倍增因子
中子入射涂硼正比管与其内壁10B薄膜发生10B(n,α)7Li核反应，生成的α粒子和7Li离子使管内P10 (Ar + 10% CH4)气体分子电离形成原初电子–离子对。正比管加上高压后，阳极丝附近的强电场可使得原初电子–离子对再次与工作气体作用产生二次电子。就单个原初电子而言，它沿途产生的二次电子数N按下式增加
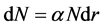(1)
上式中α称为第一汤森系数，是距阳极丝r的函数。根据正比管倍增因子的定义，倍增因子M应满足
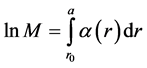(2)
该积分应遍及倍增可能发生的区域，r0称为临界半径或倍增始点，a为正比管阳极丝半径。理论和实践表明：与α联系更为密切的是约化电场ε，它定义为场强E与气压p的比E/p。约化电场国际单位为V/(m∙Pa)或V/(μm∙atm)，易知1.0 V/(μm∙atm) = 9.87 V/(m∙Pa)。从热力学知在确定的状态下气体的分子数密度n与压强p呈正比关系，因此ε通常还写为ε = E/n，其国际单位是V∙m2，常用的有汤森(Td)，且1.0 Td = 1.0 × 10−21 V∙m2。据此可知常温下两个常用单位之间关系为1.0 Td = 0.0248 V/(μm∙atm)。上式(2)也可写为
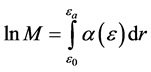(3)
其中ε0、εa分别为倍增始点处临界约化电场和阳极丝表面约化电场。由电磁学可知圆柱形正比管内离开阳极丝距离r处的约化电场满足
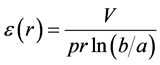(4)
其中V是极间电压，b为阴极管内半径。将(4)代入(3)可得圆柱形涂硼正比管倍增因子
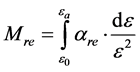(5)
上式右边αre = α/p (或αre = α/n)称为约化汤森系数，国际单位分别为m−1∙Pa−1或m2，常用单位Td/V；左边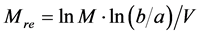
称为约化倍增因子，它是一个由所加电压和正比管尺寸决定的量，国际单位为V−1。
3. 约化汤森系数、约化倍增因子和约化电场关系的统一
3.1. 三类αre-ε和Mre-εa关系
由式(5)可知对给定的αre-ε假设，约化倍增因子仅与正比管阳极丝表面约化电场εa有关。前人提出的三类αre-ε关系，及对应Mre-εa表达式经统一改写后列于表1。
3.2. 统一性分析
3.2.1. 正比计数管倍增条件
正比计数管要实现倍增，必须满足M > 1或者Mre > 0，从表1可知正比计数管的倍增条件就是阳极丝表面处约化电场应大于临界约化电场，即εa > ε0。一般临界约化电场ε0的值与填充气体种类及组分有关，对P10气体而言ε0 = 4.84 V/(μm∙atm) = 195.16 Td，且随着CH4含量的增高ε0逐渐增大[19] 。
Table 1. Three kinds of common relationship of αre-ε and Mre-ε
表1. 三类常见的αre-ε、Mre-εa关系式
3.2.2. 三种关系内部的统一性
两种线性关系区别就在于倍增始点αre的值，L2对应5.73 Td/V而L1为0。下文将看到其实他们来源于同一种αre-ε关系式，只是近似级数不同而已。幂指数关系P1、P2的统一性就更明显了：P1就是P2中d = 1/2时的特殊情况，因此A3 = A4。自然指数关系E2是E1中B5 = ε0的特殊情况；适当的近似后E2和E3也可以统一起来，其系数之间的关系取决于近似条件。
3.2.3. 线性关系与幂指数关系的统一性
幂指数关系与线性关系之间的过度可借助图线说明。文献[22] 中Diethorn公式对P10的实验结果为A1 = ln2/23.6 = 0.02937 V−1，据此可以做出线性关系关系假设L1下，对应于不同d值的Mre-εa关系曲线如图1所示。
从图1可以看出，随着d的取值逐步接近1.0，Mre-εa关系曲线也越来越接近Diethorn公式。换句话说，线性关系L1是P2中d取值趋近于1时的特殊情况，线性关系L和幂指数关系P是统一的。
3.3. 三种αre-ε关系之间的统一性
1) 1985年Aoyama等[15] 提出的三参数αre-ε关系式：
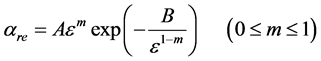(6a)
上式中A、B、m是与气体性质有关的常数，这样约化倍增因子就可写为
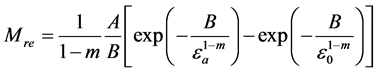(6b)
当m = 1时αre = A1ε此即线性关系L1；而当m = 0时得到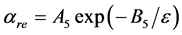
就对应自然指数关系E1；m = 1/2时做1级近似便得幂指数关系P1。对P10和Xe + 5% CO2气体，m = 12。
2) 1995年Segur等[23] 针对非均匀电场改进了三参数Mre-εa关系，提出场梯度模型
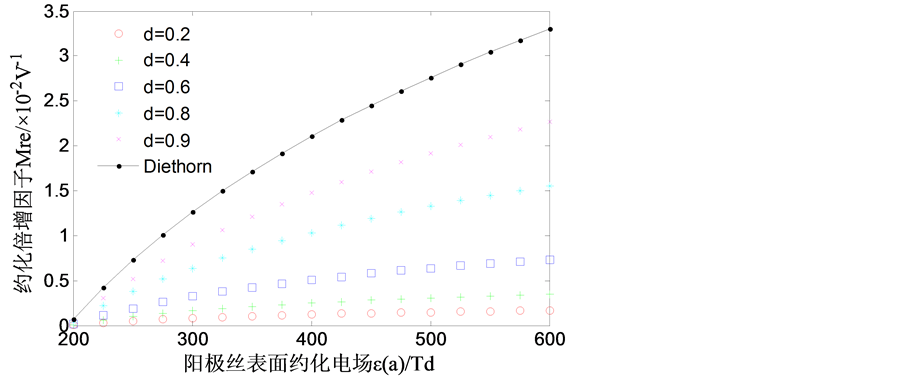
Figure 1. Curves of “Mre-εa” due to various “d” under exponential relationship
图1. 幂指数关系下不同d值对应的Mre-εa关系曲线
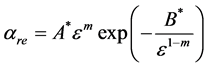(7a)
对应的约化倍增因子为
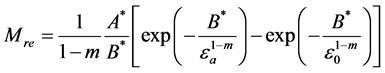(7b)
与(7)式不同的是，(8)式中的系数A*、B*不再是常数，他们依赖于气体的压强p。
3) 1999年Mazed等[19] 提出的半微观的αre-ε关系式：
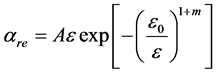(8a)
由此得出相应地的Mre-εa关系可写为
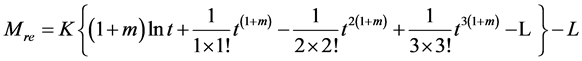(8b)
式中t = εa/ε0，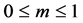
且最佳取值为2/3；K和L的值仅与气体种类、组分有关，对P10有K = 0.02004 V−1，L = 7.87 × 10−3 V−1。当m = 0时展开式(9a)得
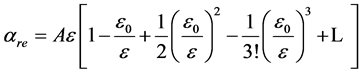(9)
不难看出零级近似对应着线性关系L1，一级近似对应着线性关系L2。可见上述三种关系均为以上三个通用关系在特定条件下的近似，这表明上述线性、幂指数和自然指数三种关系之间有着良好的一致性。
4. 约化汤森系数、约化倍增因子和约化电场关系图
4.1. 临界约化汤森系数
根据正比管中气体放大(倍增)的概念，正比计数管倍增也对该处的约化汤森系数αre有了对应的限制，限制条件取决于具体的αre-ε关系。从表1可知αre随ε增大而增大，从而正比管倍增中类似地也存在临界约化汤森系数Σ，且Σ = αre(ε0)。不难看出，表1中那些关系对应的Σ表达式依次为A1ε0，0，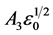
，
，
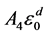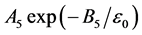，A6/e，A7/e。可见自然指数关系下Σ有固定的值，而线性关系是自然指数的一种特例，幂指数关系下Σ与具体所取的指数d (0 < d < 1)有关。
4.2. 常用αre-ε和Mre-εa关系图解
4.2.1. 常用αre-ε关系的系数确定
以P10气体充入正比计数管为例，ε0 = 195.16 Td，A1 = 0.02937 V−1，可得Σ = 5.732 Td/V。据此可得出对于这种气体在上述部分关系下对应的系数A列于表2：
4.2.2. 常用αre-ε、Mre-εa关系曲线图
对于表2中的关系L1、P1和E1-E3，取特定参数的正比计数管(V = 1 KV、b = 2 cm、a = 10 μm、p = 1 atm)后有εa = 13.16 V/(μm∙atm) = 530.6 Td。以P10气体填充时，可作αre-ε关系曲线如图2。
从式(1)可知，第一汤森系数是一个原初电子在其单位长度路径上产生的二次电子个数，而约化汤森系数αre = α/p，它可认为是特定气压下一个原初电子产生的二次电子个数。若将自然指数关系统一为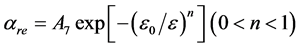
，则在相同约化电场处，参数n在减小的过程中αre随之减小，也就是说对一个原初电子其单位长度路径上产生的二次电子个数估计越来越保守。在这种估计中幂指数关系P1和线性关系L1均介于三个自然指数关系之间，可能因线性关系L1形式简单且更容易被人们接受，因而对应的Diethorn公式在计算平均倍增因子时得到了广泛的应用。
在表2中几种假设下，约化倍增因子随阳极丝表面约化电场的变化曲线如图3所示。
从图3可知：1) Mre随εa增大而增大；2) Mre随εa增加的速度因αre-ε关系而异；3) 不同αre-ε关系下得到某一εa下的Mre值相差不大。换句话说，只要正比管的尺寸和工作参数确定，倍增因子取值与具体选用何种假设关系不大，Diethorn提出的简单线性关系L1正是因此得到广泛应用。
5. 结论
本文首先提出了约化汤森系数、约化倍增因子、临界约化场强与临界约化汤森系数的概念，通过对三类约化汤森系数与约化电场的关系：线性关系、幂指数关系和自然指数关系的分析，得出如下结论：
1) 描述约化汤森系数、约化倍增因子和约化电场之间的三类关系具有良好的统一性；
2) 正比管中存在临界约化电场和临界汤森系数，其取值因αre-ε关系而异；
3) 正比管中约化倍增因子随阳极丝表面电场递增，其增速受αre-ε关系影响，但倍增因子取值变化很小。
Table 2. Common relationship of αre-ε and value of their coefficient
表2. 常见αre与ε关系式及其对应系数值
注：表中A5、B5的值用到了αre(ε0) = 5.732 Td/V、αre(εa) = 15.581 Td/V和εa = 530.6 Td。
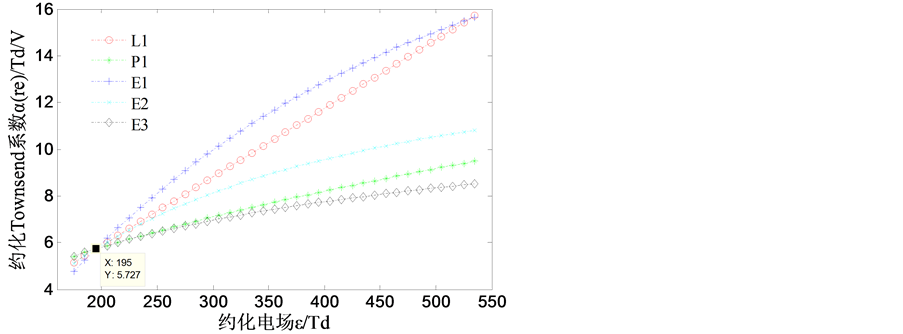
Figure 2. Curves of some relationships between reduced Townsend coefficient αre and reduced electric field ε
图2. 几种约化汤森系数与管内约化电场关系曲线
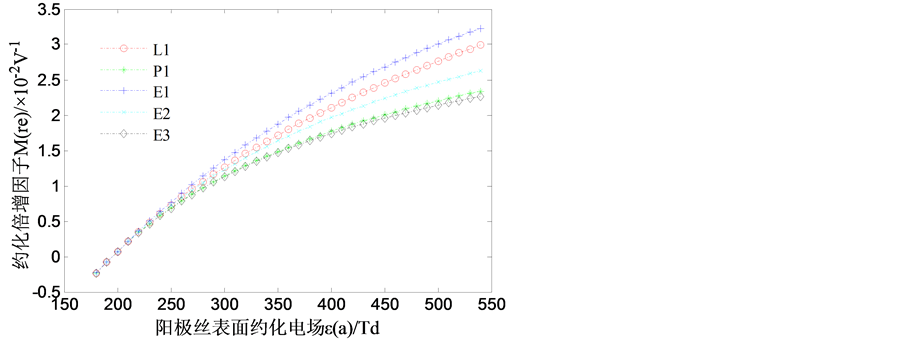
Figure 3. Curves of some relationships between reduced multiplication factor Mre and the reduced electric field on the anode surface εa
图3. 几种约化倍增因子与阳极丝表面约化电场关系曲线
正比管的倍增因子值与采用何种假设关系不大，因而Diethorn提出的线性关系得到广泛应用。
致 谢
本文获国家自然科学基金(41064002)资助，在此表示感谢！
基金项目
国家自然科学基金资助项目(41064002)。
NOTES
*通讯作者。