1. 引言
可拓学是研究事物的可拓性与开拓规律和方法的科学[1] [2] 。它的基本思想是利用物元理论和可拓集合理论，结合各应用领域的理论和方法去处理该领域中的矛盾问题，以化不可行为可行，化不可知为可知，化不属于为属于，化对立为共存。
物元是描述事物的基本元素，用一个有序三元组R = (N, c, v)表示，其中N表示事物的名称，c表示特征的名称，v = c(N)表示N关于c所取的量值[3] 。
一个客观的物有无数特征，用n维物元表示其有限特征及对应的量值，即
(1)
2. 基于可拓学的采场顶板稳定评价物元模型
影响采场顶板稳定性等级的因素有很多，最突出的实测RQD值、单轴抗压强度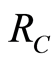
、节理裂隙频度J、采场暴露面积和岩体的声波速度V等诸多方面[4] -[6] 。在此，选取N作为表示采场顶板稳定的等级标准；
表示影响采场顶板稳定等级水平的特征因子；
表示该特征因子所对应的量值。根据n维物元的定义，采场顶板稳定等级物元可用下式描述：
(2)
待评物元模型的建立包括三方面的内容：确定经典域、节域和待评物元，分叙如下。
2.1. 经典域
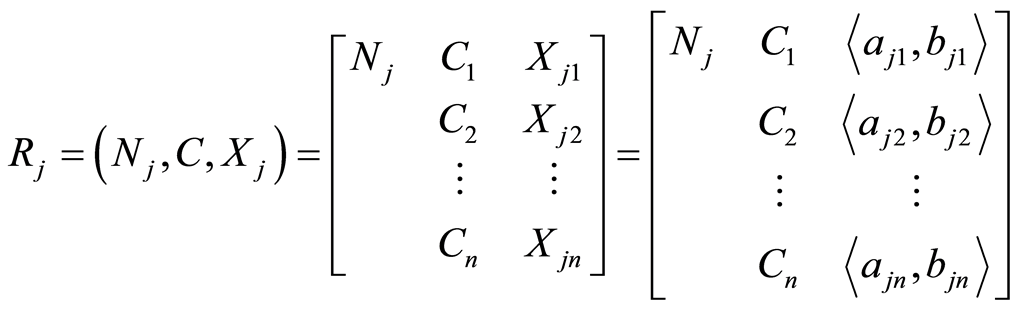(3)
式中：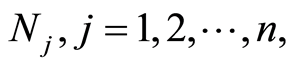
表示所划分的顶板稳定性等级水平；
表示影响等级水平的特征因子；
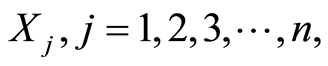分别为相应的顶板稳定性等级
关于
所确定的量值范围，即经典域
。
2.2. 节域
(4)
式中：P表示采场顶板稳定性等级的全体；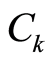
为P的特征参数，
表示
的所有取值范围，即经典域
。
2.3. 待评物元
把待评顶板稳定等级因子的作用资料用物元表示，就称之为采场顶板稳定等级水平的待评物元。
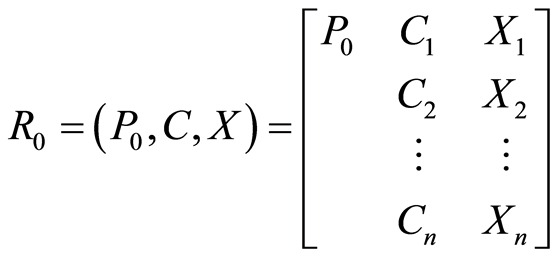(5)
式中：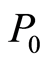
表示待评采场顶板的稳定性等级水平，
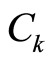为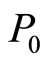
的特征参数，
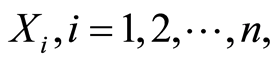表示特征参数
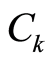的具体数值，即从待评采场所收集到的具体工程数据。
2.4. 计算关联度
1) 关联函数表示物元的量值取为实轴上一点时物元符合要求的程度，它可以是线性的，也可以是非线性的，在此，采用下面非线性函数作为关联函数：
(6)
其中：
，
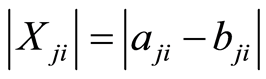
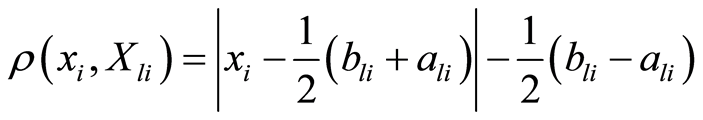
2) 根据可拓数学的关联函数，待评物元
关于采场顶板稳定性等级
的综合关联度为:
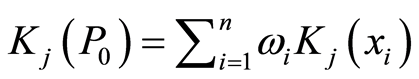(7)
式中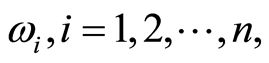
为多指标特征参数的权重系数，这里可以使用德尔菲法来确定。
表示待评物元
关于特征参数的具体值
属于顶板稳定性等级
的程度。
2.5. 采场顶板稳定性的综合评价标准
将在采场实际测得的数据资料分别代入公式(6)中，计算出相应的关联度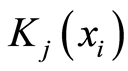
，然后再用公式(7)计算出待评物元
关于采场顶板稳定性等级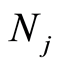
的综合关联度
。若
(划分了m个等级)，则评定待评物元的稳定性等级水平属于等级j。若对一切j有
，则表示待评物元的质量等级不在所划分的各质量等级之内，应重新调整特征参数和权重系数，再重复上述步骤。
3. 采场顶板稳定性评价实例
云南某矿区为一集钨、钼、铋等多种有色金属于一体的缓倾斜厚矿床，区内构造简单，主要为褶皱和断裂构造。矿体主要为花岗岩接触交代矽卡岩型钨矿、夹在变玄武岩层中的层状矽卡岩钨矿。其中I号矿体赋存的部位下盘为花岗岩，花岗岩的稳固性随风化程度的不同有很大差异，由松散极不稳固至坚硬稳固，f = 3~15，上盘多为变基性玄武岩、大理岩，局部为灰质白云岩，围岩稳固性较好，f = 10~15。而Ⅱ号矿体上下盘多为变基性玄武岩、大理岩，局部为灰质白云岩或矽卡岩，围岩稳固性较好，f = 10~15。矿体一般由矽卡岩矿石组成，矿石致密坚硬，稳固性好，f = 10。矿床水文地质条件以溶蚀裂隙充水为主，属于简单–中等类型。
3.1. 影响采场顶板稳定性因素的选取
影响采场顶板稳定性的因素大体上可以归结为两个方面，即自然因素和人为因素。自然因素主要包括地质构造、水文地质条件、岩体结构及其发育状况等；人为因素主要包括采场跨度、采场暴露面积以及所使用的采矿方法等[7] 。由于各个采场中每一个因素所起的作用大小不确定，故而在此选取7个有代表性的影响因素作为评价的指标。它们分别是：单轴饱和抗压强度、体积裂隙数、裂隙间距、RQD、采场允许暴露面积、应力折减系数和采场的当量尺寸。以上各指标对采场顶板稳定性的影响的单因素指标如下表1所示。
由表1可得顶板稳定性等级的经典域为：
Table 1. Single-factor evaluation index of roof stability
表1. 顶板稳定性的单因素评价指标
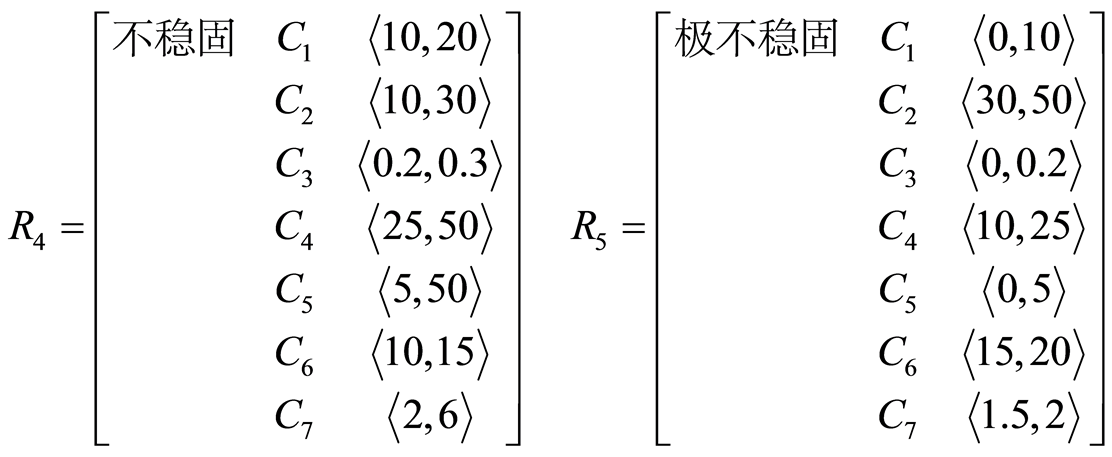
相应的节域为：
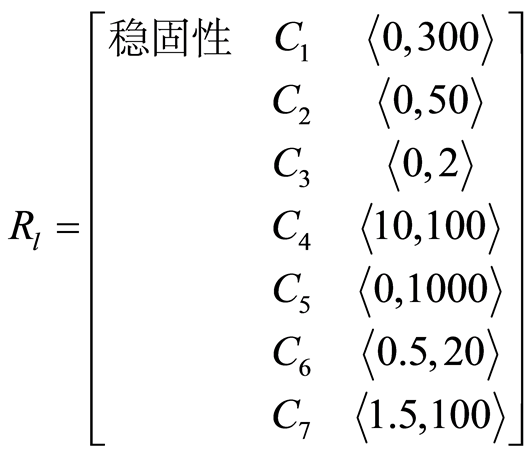
其中：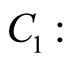
单轴饱和抗压强度(MPa)，
体积裂隙数，
裂隙间距(m)，
RQD(%)，
采场允许暴露面积(m2)，
应力折减系数，
采场的当量尺寸(m)。
3.2. 采场顶板稳定性评价分析
根据现场获取的四个采场的数据如表2所示。
将各采场表示为待评物元为：
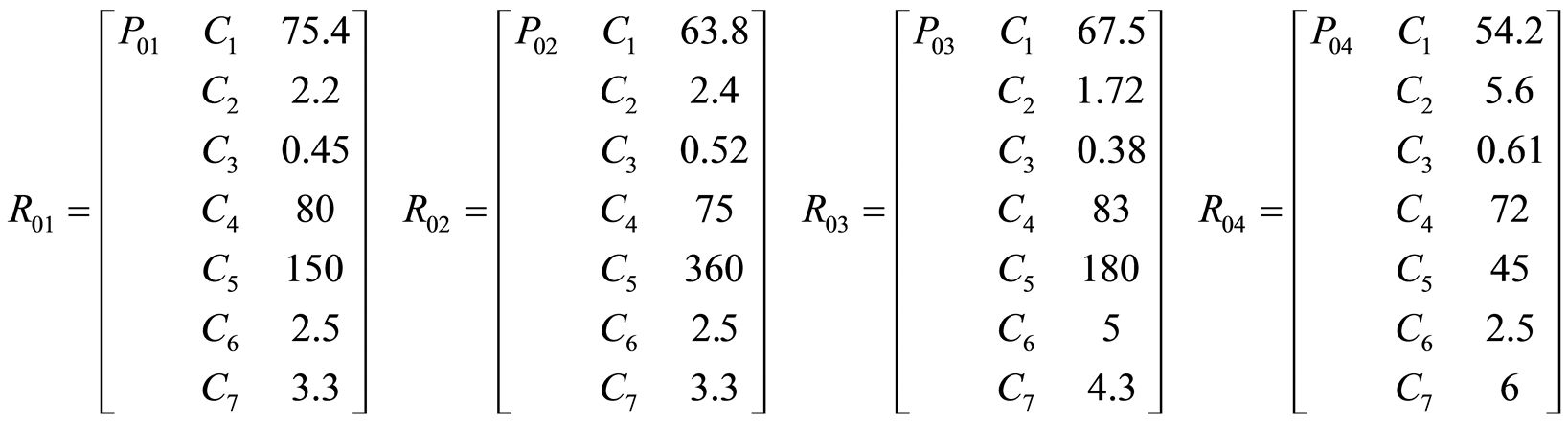
根据(6)式计算出各因素对采场顶板稳定性影响的关联度。其结果如表3所示。
Table 2. Evaluation index value of actual stopes
表2. 实际采场稳定性评价指标值
Table 3.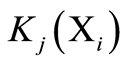 
{i = 1,2,3,4,5; j = 1,2,3,4,5,6,7}
表3.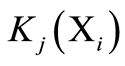 
{i = 1,2,3,4,5; j = 1,2,3,4,5,6,7}
根据参考文献[8] 中计算权重系数的德尔菲法，获得第二轮专家咨询统计结果，如下表4所示。
将以上各要素的平均分值进行归一化，以得到其权重系数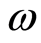
。故可得各权重系数分别为：0.203、0.164、0.155、0.138、0.200、0.066、0.074。
根据公式(7)计算出待评物元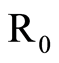
关于采场顶板稳定性等级
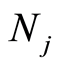的综合关联度。其结果如表5所示。
根据3.5中采场顶板稳定性的综合评价标准，可得以下结果：
，
，
，
，
。
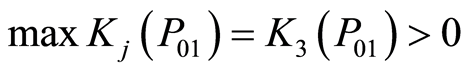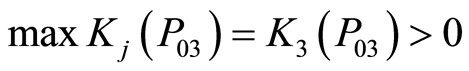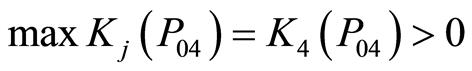根据以上结果可知：1号、2号和3号采场顶板稳定性均为中等稳固，而4号采场则不稳固。这与实际情况基本一致。同时根据关联度所反映的稳定性接近度，可以发现1号采场中等稳固趋于稳固状态，2号和3号采场中等稳固趋于不稳固，这也为采场的稳定性评价及工程实际提供了更加有效的参考依据。
Table 4. The second round statistical result of expert consultation
表4. 第二轮专家咨询统计结果
4. 结语
可拓学在岩体质量的评价方面已经得到广泛的应用，顶板稳定性评价所得到的结果比较接近实际情况，反映了其评价结果的客观性。但是在地质构造非常复杂的情况下，有可能使评价结果可能因岩体中的评价因素(指标)的信息缺失造成一定误差。为此，在条件允许下因该考虑尽可能多的评价因素(指标)，并采用主客观综合赋权重的方法来进一步完善可拓学在这一领域的应用。
基金项目
国家自然科学基金(编号：51204205)；教育部博士点基金资助项目(编号：20110162120056)。
NOTES
*通讯作者。