1. 引言
目前，随着我国“西电东送、南北互供、全国联网”电力发展战略的实施，大量特高压交直流输电系统相继开始建设或规划。西南至广东、华中和华东的特高压输电线路走廊均将途经山脉起伏、地形复杂、雷电活动频繁和山区土壤电阻率高的地区，并且由于特高压输电线路的杆塔较高，引雷面积较大，输电线路电压等级对耐雷水平要求影响显著，使得特高压输电线路的防雷设计面临严峻的考验[1] 。
防雷与接地技术关系密切，土壤电阻率对特高压输电线路防雷有很大的影响。研究土壤电阻率对雷击杆塔顶端时塔顶电位的变化规律对特高压输电线路的防雷设计有指导意义。为了能够更准确地计算土壤电阻率对塔顶电位的影响，首先需要建立准确的接地电阻模型。目前杆塔的冲击接地电阻通常由杆塔的工频接地电阻乘以冲击系数来得到[2] ，依此得到的冲击接地电阻为一个与土壤电阻率成正比的恒定值，显然不能反应杆塔冲击接地电阻随雷电流波过程变化的特性。在冲击电流下，杆塔的接地电阻显然不是常数，应是电流和时间的函数，并不是与土壤电阻率呈简单的线性关系，因此对土壤电阻率高的山区，做防雷计算时更应考虑冲击接地电阻随时间变化这一特性。因此本文采用考虑了火花效应和电感效应的接地体等效时变模型来模拟雷电作用下的接地电阻。
本文建立了接地体等效时变模型，建立了特高压输电线路雷击仿真计算模型，在此基础上分析了雷击杆塔顶端时土壤电阻率对塔顶电位的影响规律。
2. 仿真计算模型
为了研究雷击特高压输电线路杆塔塔顶时土壤电阻率对塔顶电位的影响规律，需要建立准确的冲击接地电阻模型，特高压输电线路杆塔的杆塔模型、线路模型，以及雷电流的模型。
2.1. 接地电阻模型
通常定义的接地电阻为工频接地电阻，是指一定的电流经接地极流入大地时，接地极与无穷远处零电位面之间的电位差V与电流I的比值[2] 。当接地装置流过雷电流时，它所呈现的冲击接地电阻一般并不等于它的工频接地电阻，这是由冲击作用下接地体的电感效应和火花效应所致。雷电流的幅值大(数十千安)，接地体的电位很高，会发生局部火花放电，土壤等效电导率变大，其效果相当于增大了接地体的尺寸，越靠近电流注入点接地体电位越高，土壤的击穿区域也就越大，即等值半径越大，因此接地极周围土壤的击穿区域形状呈锥形[3] [4] 。因此每一点处接地体的泄露电导和对地电容并不相同。
在冲击电流的作用下，接地体可以看成是由电感、电容、电导和电阻组成的梯形等值电路[5] ，如图1所示。图1中Ri和Li分别表示第i段接地体的自身电阻和电感，Ci和Gi分别表示各段接地体的对地电容和泄漏电导。
在计算水平接地体冲击接地电阻时，通常可取该电阻Ri为常数。本文取单位长度接地体电阻为0.05 Ω/m [5] 。其他几个参数的计算公式[6] 如下：
单位长度电感公式简化为：
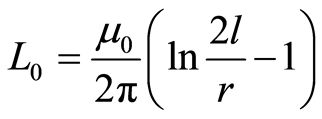(1)
单位长度伸长接地体对地电导为：
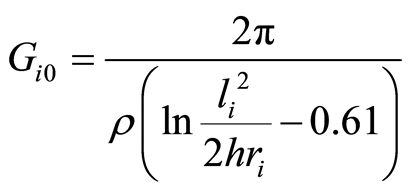(2)
各段接地体单位长度对无穷远零位面的电容为
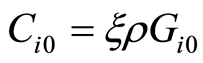(3)
式中：μ0为真空的导磁系数，r为接地体半径，l为接地体长度，Gi0为第i段伸长体单位长度的对地电导；li为接地体第i段的长度；ρ为土壤电阻率；h为接地体埋深。ε为土壤介电系数，在实用范围内ε = 9 × 8.86 × 10−12。
由于火花区域边界的电场强度为土壤的临界击穿场强，则各段导体考虑火花放电后的等值半径可通过式(4)求得[3] ：
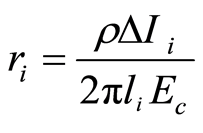(4)
式中：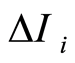
为通过第i段导体向大地流散的电流；Ec为土壤临界击穿场强。实时读取每段导体的散流电流来计算那个时刻的接地体等效电阻ri，将ri值代入式(2)和(3)即可获取各段接地体的泄漏电导Gi和对地电容Ci。进而可求出瞬时的接地电阻的值。这样便模拟出了冲击接地电阻的时变特性。
本文利用ATP-EMTP的TACS[7] 实现接地体对地电导Gi的控制(对地电导的影响比对地电容的影响大得多，这里仍把对地电容Ci作为不变量来处理)，这种方法充分考虑了土壤电阻率及流过接地体的电流幅值与频率对冲击接地电阻的影响。
2.2. 杆塔模型
由于特高压杆塔本身较高(一般在50 m以上)，波沿杆塔传播时，沿塔身的单位长度电感和单位长度
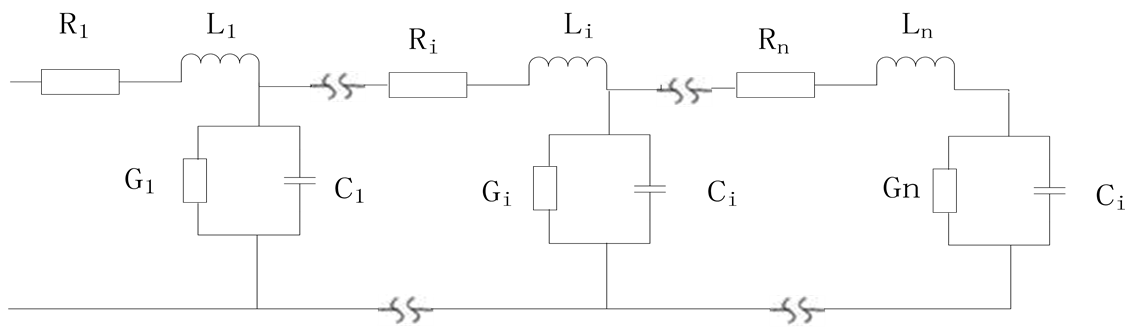
Figure 1. Representation of a grounding electrode with nonuniformly lumped parameters
图1. 非均匀分布的接地体等效电路模型
电容是变化的，沿杆塔分布的波阻抗也是变化的。采用集中电感模型和单一的波阻抗模拟杆塔亦会带来一定的误差。日本学者Yamada T.，Hara T.，西班牙学者Martinez，J.A.等对杆塔进行了冲击试验研究[8] -[11] ，测量了杆塔不同部位的阻抗值，在试验基础上建立了多波阻抗模型来模拟输电线路的杆塔，如图2所示。模型既计及了杆塔参数随高度的变化，又包含了波在杆塔上的传播特性，因此其计算准确度有很大提高。图3为±800 kV直流杆塔结构，而多波阻抗杆塔模型如图2所示，ZAi为杆塔横担波阻抗；ZTi为不同高度处杆塔主体的波阻抗；ZLi为不同高度杆塔支架的波阻抗。
2.3. 线路模型
由于雷电流波形中含有丰富的高次谐波，不同频率的谐波分量在线路中传播时的衰减和畸变各不相
Figure 2. Multi-wave-impedance model
图2. 多波阻抗模型
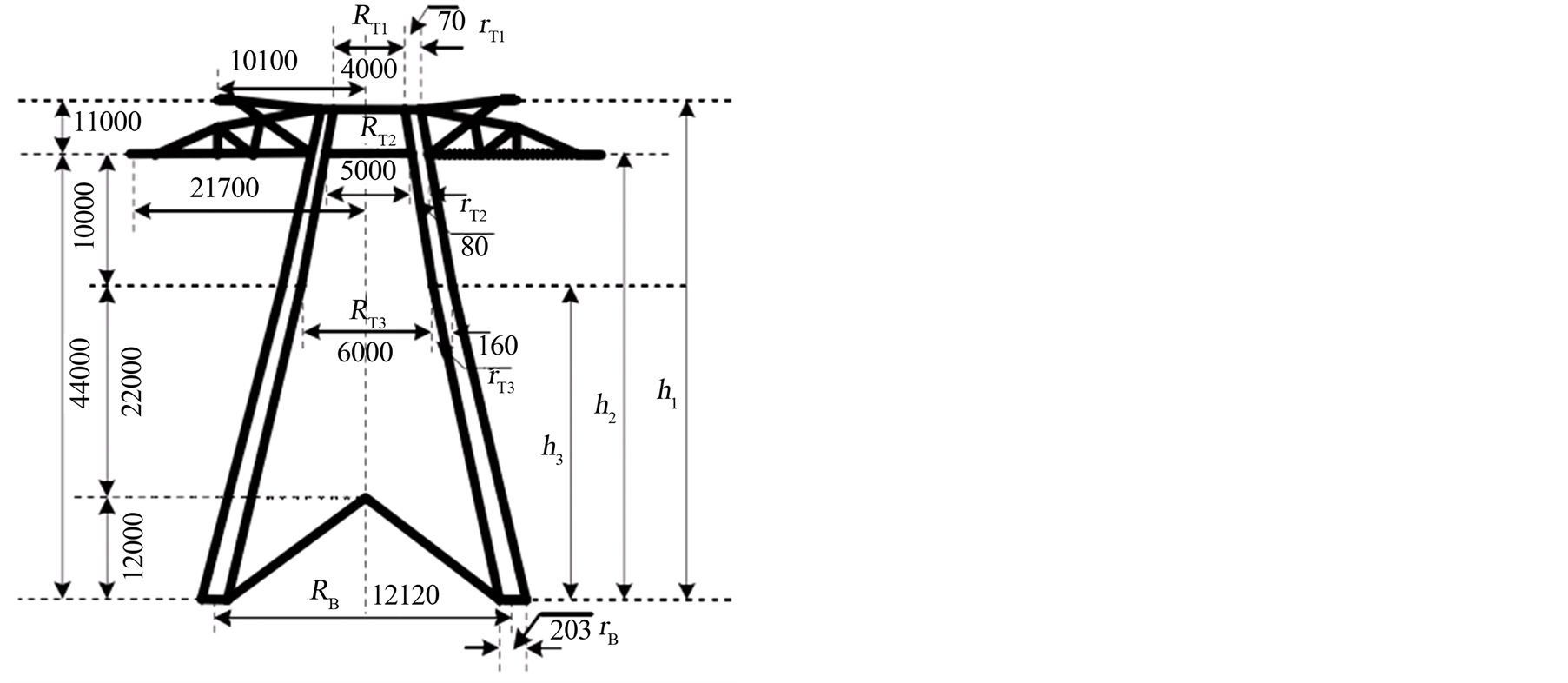
Figure 3. Geometry and dimensions of the ±800 kV transmission tower (unit: mm)
图3. ±800 kV直流杆塔结构及几何尺寸(单位：mm)
同，因此本文采用2条导线2条地线具有频率特性的架空线模型来模拟线路，由ATPDraw中的标准元件LCC计算模拟，能够直接用参数表示架空线内径、外径、水平和垂直位置等各种关系，并且能直接计算导线与地线间的耦合系数，具有较高的计算精度。本文所取的±800 kV线路参数为：导线型号为6 × LGJ630/45；避雷线型号选择LG120/25，档距选取500 m。
2.4. 雷电流模型
雷电波采用双指数表达式，波型为2.6/50 μs，负极性为主要波形，幅值为240 kA。雷电通道波阻抗取300 Ω。
3. 仿真结果及其分析
本文以±800 kV特高压直流输电线路为例，计算雷击塔顶时塔顶电位随土壤电阻率的变化情况。仿真中选取的土壤电阻率取值范围为100~2200 Ω·m。
根据上面建立的杆塔模型与冲击接地电阻等模型与参数，得到雷击特高压输电线路塔顶时，塔顶电位随土壤电阻率变化的规律如图4所示。
由图可知，当杆塔所受雷电流幅值和接地体的几何尺寸一定时，塔顶电位随土壤电阻率的增大而增大。
当土壤电阻率较小时，塔顶电位随电阻率增加而升高的速度较快，而当电阻率较大时，塔顶电位升高的速度减小。这是因为当土壤电阻率较小时，容易将电流散到土壤中去，随着土壤电阻率的增加，接地体周围场强增加的比较小，土壤的击穿程度不大，使冲击接地电阻变化接近线性，塔顶电位随土壤电阻率的改变比较明显。当土壤电阻率大于1000 Ω·m时，土壤的导电性能下降，只有通过击穿土壤形成火花区才能将冲击电流流散出去。随着土壤电阻率增加，使接地体周围的场强增加较多，导致接地体的等效半径增加较多，削弱了土壤电阻率对冲击接地电阻的影响，使得接地电阻的变化趋势变得平缓，从而使塔顶电位变化缓慢。
目前在工程上在高电阻率地区有时采用人工改善土壤的方案来降低冲击接地电阻，其中包括以下几种方法：用电阻系数较低的土壤进行置换、采用人工方法提高接地极周围土壤的导电率、使用降阻剂[12] 。或者采取将接地线牵引到低电阻率区域再接地的方案。当电阻率比较大时，如果接地点土壤电阻率降低的不是很明显，则可能会达不到明显的效果。比如，在山区土壤电阻率为2200 Ω·m，而接地点的土壤电阻率只能降低到1500 Ω·m，此时的塔顶电位仅仅下降了6.25%。因此应根据接地点的土壤电阻率情
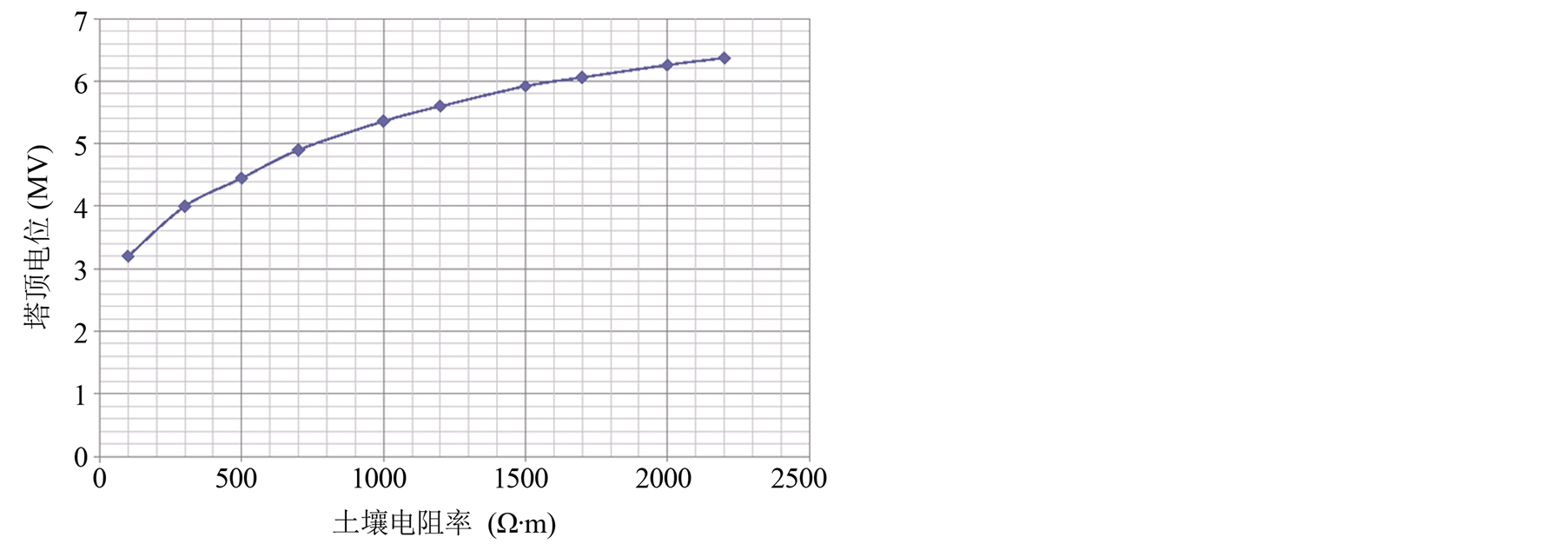
Figure 4. Tower potential varying with various soil resistivity
图4. 塔顶电位随土壤电阻率的变化规律
况来选取防雷方案，否则会达不到预期的效果，造成经济上的浪费。
4. 结论
本文在利用充分考虑火花效应和电感效应的接地体时变模型，并搭建考虑波传播过程的杆塔模型以及线路模型，对高电阻率地区特高压输电线路进行建模。在此基础上，研究了特高压输电线路雷击塔顶时塔顶电位随土壤电阻率变化的情况。得到以下结论：
1) 输电线路接地装置冲击特性的好坏直接影响线路的防雷性能。本文采用冲击接地电阻的时变模型，能更准确地计算雷击特高压输电线路在塔顶遭受雷击时塔顶电位随着土壤电阻率变化的规律；
2) 塔顶电位随土壤电阻率的增加而升高。当土壤电阻率较小时，塔顶电位随电阻率增加而增加的速度较大，而当电阻率较大时，增加的速度减小。这是由于不同的土壤电阻率情况下土壤火花电离程度不同引起的；
3) 特高压交直流输电系统，其线路走廊多通过接地电阻率高的山区，如果土壤电阻率比较高，通过更换接地点处的土壤或者将接地体牵引至低电阻率地区来降低接地点处土壤电阻率，从而来降低塔顶电位提高耐雷水平这种方案可能达不到明显的效果。这时应该采取其他的降低接地电阻的方案，因地制宜。