1. 引言
数据包络分析(DEA, Data Envelopment Analysis)是由A. Charnes、W. W. Coopor和E. Rhodes于1978年提出的一种系统分析方法,适合对若干同类型的具有多输入、多输出的部门(称作决策单元,即Decision Making Units,简记为DMU)进行相对效率评价和比较分析。DEA方法以相对效率概念为基础,以凸分析和线性规划为工具,应用数学模型计算比较决策单元之间的相对有效性(DEA有效)。目前,专家学者已经将DEA方法推广到具有不确定性或模糊性的多输入、多输出决策单元系统中,提出了不确定数据包络分析、模糊数据包络分析、粗糙DEA等多种模型(参见文献[1] -[4] );同时,这些模型被应用于许多领域(参见文献[5] -[7] )。本文通过实例讨论模糊DEA在高职院校办学效益评价中的具体应用。
2. 模糊DEA模型概述
对于基本DEA模型CCR(参见文献[1] [2] ),有“基于输入”和“基于输出”两种形式。“基于输入”是指在保持产出(输出)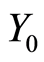 基本不变的情况下将投入(输入)
基本不变的情况下将投入(输入)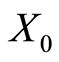 尽量减少;如果已经无法减少,则说明决策单元DMU0是有效的。“基于输出的CCR模型”,是在保持投入(输入)
尽量减少;如果已经无法减少,则说明决策单元DMU0是有效的。“基于输出的CCR模型”,是在保持投入(输入)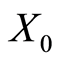 基本不变的情况下将产出(输出)
基本不变的情况下将产出(输出) 尽量扩大;如果已经无法扩大,则说明决策单元DMU0是有效的。当输入输出指标用模糊数(常用的是三角模糊数,参见[8] )表示时,相应的评价模型被称为模糊DEA(Fuzzy DEA)。
尽量扩大;如果已经无法扩大,则说明决策单元DMU0是有效的。当输入输出指标用模糊数(常用的是三角模糊数,参见[8] )表示时,相应的评价模型被称为模糊DEA(Fuzzy DEA)。
本文沿用文献[1] 中的记号,对于模糊数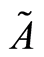 和实数
和实数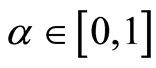 ,
,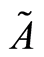 的
的 截集
截集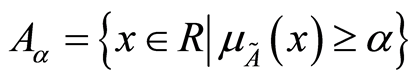 是实数域上的一个分明区间,记为
是实数域上的一个分明区间,记为 ,其中
,其中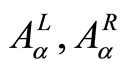 分别表示区间的左右边界。特别地,对三角模糊数
分别表示区间的左右边界。特别地,对三角模糊数 ,
, ,
,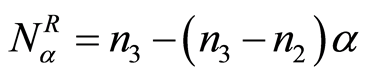 。
。
设有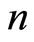 个决策单元DMUj
个决策单元DMUj ,每个决策单元的输入和输出的数目分别是
,每个决策单元的输入和输出的数目分别是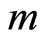 、
、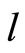 。基于输入的模糊CCR模型是对基于输入的确定性CCR模型的推广,即考虑决策单元DMUj
。基于输入的模糊CCR模型是对基于输入的确定性CCR模型的推广,即考虑决策单元DMUj 的输入输出指标由精确值变为模糊向量时的评价模型。此时,输入指标变为
的输入输出指标由精确值变为模糊向量时的评价模型。此时,输入指标变为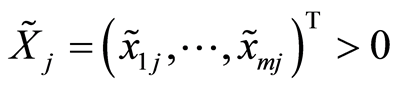 ,输出指标变为
,输出指标变为 时,被评价单元DMU0的相对有效性评价模型变为[1] :
时,被评价单元DMU0的相对有效性评价模型变为[1] :
 (M1)
(M1)
依据截集方法和DEA评价的思想,可将上述模型在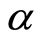 置信水平下分别转化为极大值规划和极小值规划(均为确定型线性规划):
置信水平下分别转化为极大值规划和极小值规划(均为确定型线性规划):
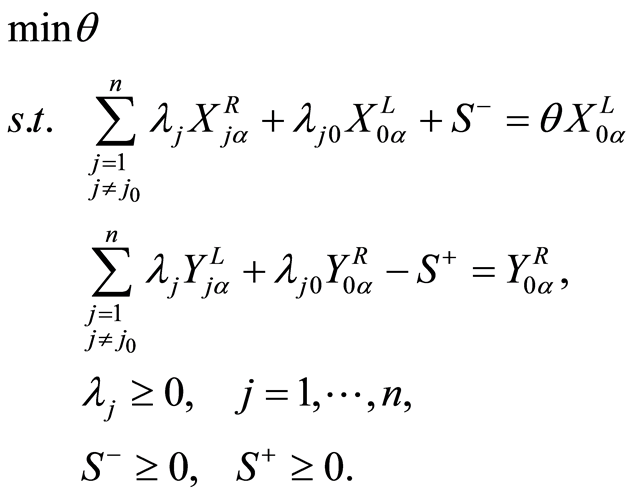 (M2)
(M2)
 (M3)
(M3)
设线性规划(M2)的最优值及最优解为 ,那么[1] :
,那么[1] :
当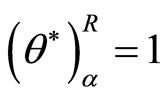 时,则被评价单元DMU0为
时,则被评价单元DMU0为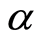 水平下的乐观弱模糊DEA有效的;
水平下的乐观弱模糊DEA有效的;
当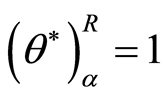 且
且 时,则被评价单元DMU0为
时,则被评价单元DMU0为 水平下的乐观模糊DEA有效的。
水平下的乐观模糊DEA有效的。
设线性规划(M3)的最优值及最优解为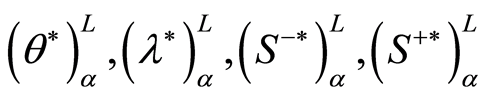 ,那么[1] :
,那么[1] :
当 时,则被评价单元DMU0为
时,则被评价单元DMU0为 水平下的悲观弱模糊DEA有效的;
水平下的悲观弱模糊DEA有效的;
当 且
且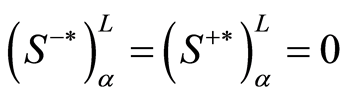 时,则被评价单元DMU0为
时,则被评价单元DMU0为 水平下的悲观模糊DEA有效的。
水平下的悲观模糊DEA有效的。
在应用上述基于输入的模糊DEA模型评价决策单元的相对有效性时,可以采用“平均置信有效性”方法对决策单元进行有效性排序,即
设在分等级置信水平 下(
下(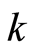 为事先指定的取点数量),决策单元相对有效性(对应前述模型M2、M3的最优值)分别为
为事先指定的取点数量),决策单元相对有效性(对应前述模型M2、M3的最优值)分别为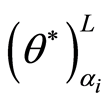 ,
, ,则决策单元的平均置信有效性为:
,则决策单元的平均置信有效性为:
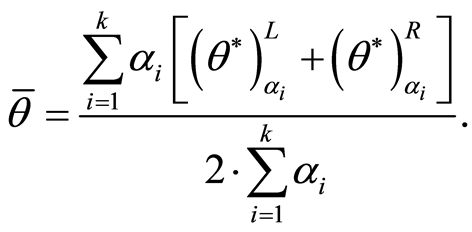
对于基于输入的模糊DEA模型来说,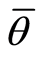 越大则决策单元的有效性越强。
越大则决策单元的有效性越强。
3. 模糊DEA应用于办学效益的评价
选择浙江省8所高职院校2012年的实际数据,应用模糊DEA方法并借助MATLAB软件进行详细计算。
3.1. 数据准备
本文使用的相关基本数据来自中国高职高专教育网(http://www.tech.net.cn/web/index.aspx)专栏“高等职业教育人才培养质量年度报告”(2012年)。尽管基本数据是真实的,但由于一些评价指标和权重具有主观性(且部分学校的个别数据缺失),为了不引起“对号入座”等不必要的麻烦,这里分别用DMU1~DMU8表示相关高职院校(不明确标示其对应学校的名称)。
3.2. 评价指标体系
将采用如下评价指标体系:三项输入指标,三项输出指标(含两项模糊指标)。
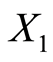 ——专任教师人数,单位:百人;
——专任教师人数,单位:百人;
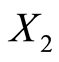 ——教职工总人数,单位:百人;
——教职工总人数,单位:百人;
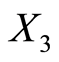 ——年度新增经费投入,单位:千万元;
——年度新增经费投入,单位:千万元;
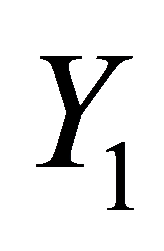 ——毕业生数量,单位:千人;
——毕业生数量,单位:千人;
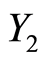 ——优质教学成果得分,用五分值评定、用[0, 5]上的三角模糊数表示;
——优质教学成果得分,用五分值评定、用[0, 5]上的三角模糊数表示;
 ——毕业生质量得分,用五分值评定、用[0, 5]上的三角模糊数表示。
——毕业生质量得分,用五分值评定、用[0, 5]上的三角模糊数表示。
对于上述输入输出指标数据,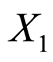 ,
,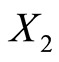 ,
,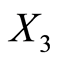 及
及 取自中国高职高专教育网公布的相关高职院校2012年度数据;
取自中国高职高专教育网公布的相关高职院校2012年度数据; 依据年度报告中省级以上精品课程、省级以上重点专业、示范实训基地及产学研基地、教学研究成果及获奖等信息综合考虑,给出评价数据(用三角模糊数表示);
依据年度报告中省级以上精品课程、省级以上重点专业、示范实训基地及产学研基地、教学研究成果及获奖等信息综合考虑,给出评价数据(用三角模糊数表示); 依据年度报告中毕业生就业率、就业去向、学生参加各种竞赛获奖、学生毕业设计及毕业实习等信息综合考虑,给出评价数据(用三角模糊数表示)。
依据年度报告中毕业生就业率、就业去向、学生参加各种竞赛获奖、学生毕业设计及毕业实习等信息综合考虑,给出评价数据(用三角模糊数表示)。
最后得到的8所高职院校各指标数据如表1所示,对于三角模糊数分别使用 ,
, ,
, ,
,
 来表示:
来表示:
3.3. 计算过程
以下采用“基于输入的模糊DEA”模型对上述8所高职院校进行办学效益评价。
根据表1中的数据,与高职院校DMU1相对应的模糊DEA评价规划为:称为(P1)

Table 1. Input and output indexes data of eight Vocational Colleges
表1. 八所高职院校输入输出指标数据

由于
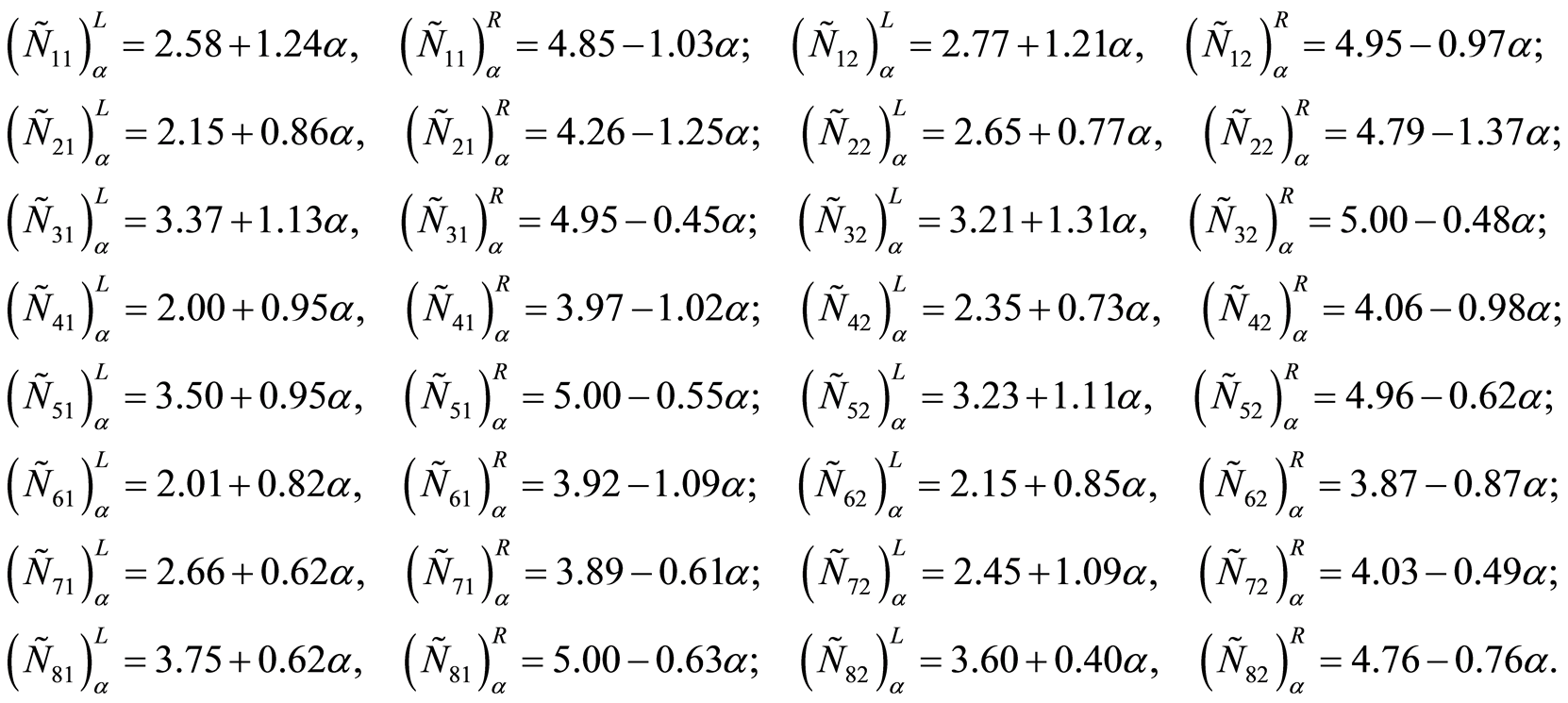
所以,依照取截集的方法,在置信水平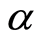 下,求解模糊规划问题(P1)可转化为求解如下两个普通线性规划问题:分别称为(P11)和(P12)
下,求解模糊规划问题(P1)可转化为求解如下两个普通线性规划问题:分别称为(P11)和(P12)
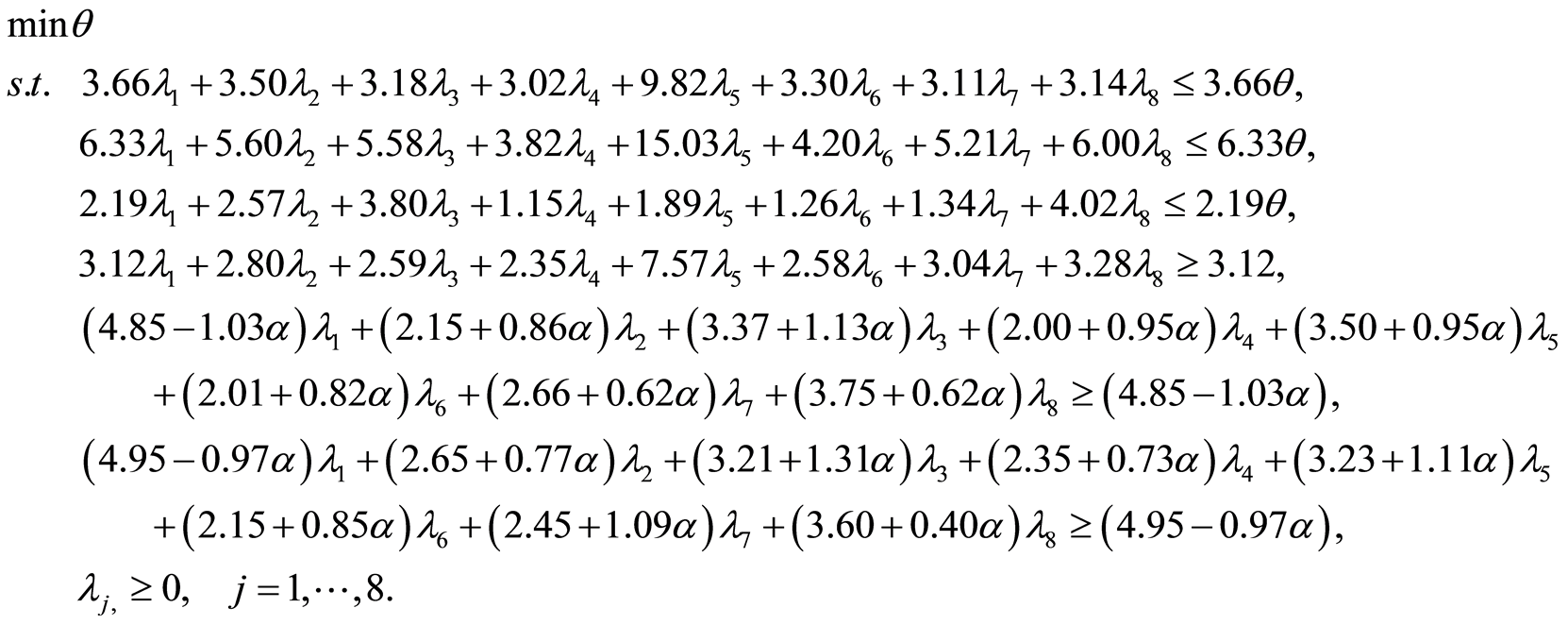
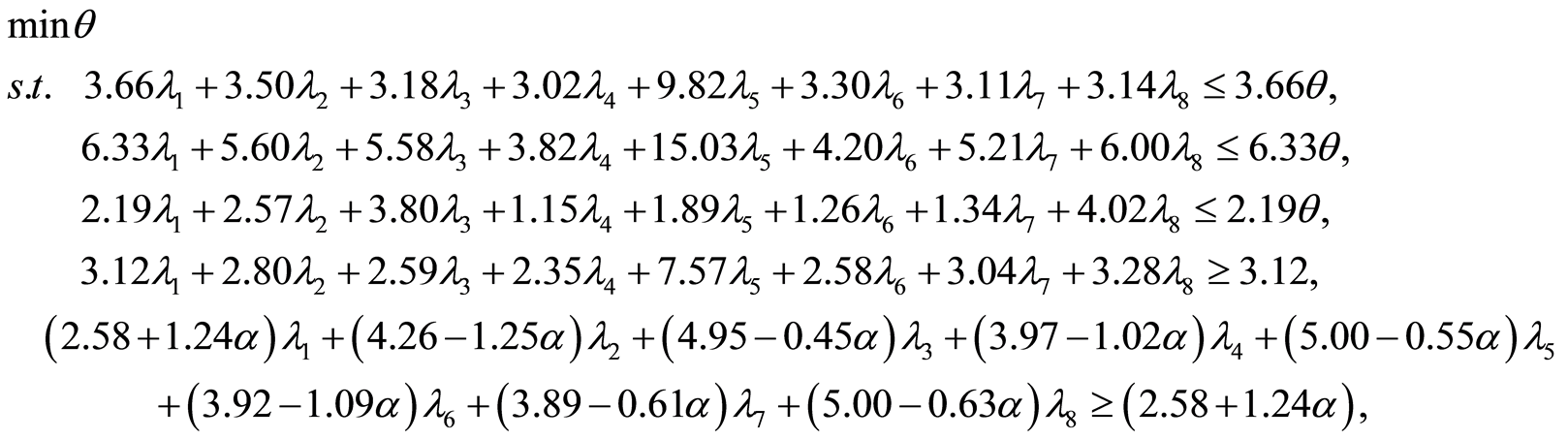
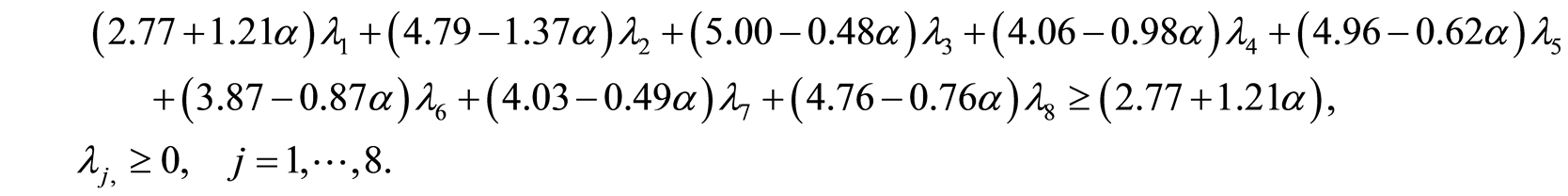
选取不同置信水平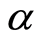 值,分别求解线性规划(P11)及(P12)可得到高职院校DMU1的模糊DEA有效区间
值,分别求解线性规划(P11)及(P12)可得到高职院校DMU1的模糊DEA有效区间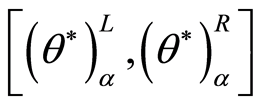 。比如,取
。比如,取 ,借助MATLAB求解(P11)、(P12)得到模糊DEA有效区间为:
,借助MATLAB求解(P11)、(P12)得到模糊DEA有效区间为: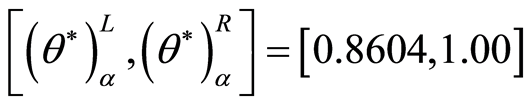 计算过程如图1及图2示。
计算过程如图1及图2示。
从图1、图2的计算结果可以看出,对于置信水平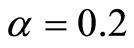 ,高职院校DMU1是“乐观模糊DEA有效的”,但不是“悲观模糊DEA有效的”。
,高职院校DMU1是“乐观模糊DEA有效的”,但不是“悲观模糊DEA有效的”。
类似地,分别取 ,0.6,0.8,1可得到高职院校DMU1的模糊DEA有效区间为:
,0.6,0.8,1可得到高职院校DMU1的模糊DEA有效区间为: ,
,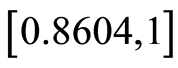 ,
, ,
,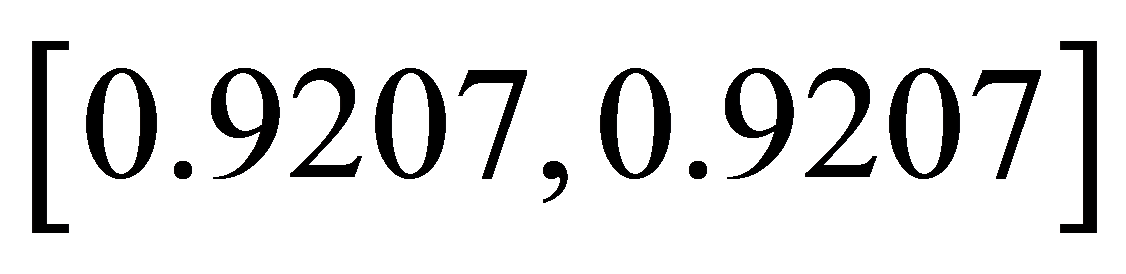 。
。
实际上,可在MATLAB中使用参数,重复使用同一段代码计算不同置信水平下DMU1的模糊DEA有效区间。含参MATLAB程序如下所示:
f = [0, 0, 0, 0, 0, 0, 0, 0, 1];
A = [3.66, 3.5, 3.18, 3.02, 9.82, 3.30, 3.11, 3.14, -3.66; 6.33, 5.6, 5.58, 3.82, 15.03, 4.2, 5.21, 6, -6.33; 2.19, 2.57, 3.8, 1.15, 1.89, 1.26, 1.34, 4.02, -2.19; -3.12, -2.8, -2.59, -2.35, -7.57, -2.58, -3.04, -3.28, 0; -(4.85-1.03*a), -(2.15 + 0.86*a), -(3.37 + 1.13*a), -(2.00 + 0.95*a), -(3.5 + 0.95*a), -(2.01 + 0.82*a), -(2.66 + 0.62*a), -(3.75 + 0.62*a), 0; -(4.95 - 0.97*a), -(2.65 + 0.77*a), -(3.21 + 1.31*a), -(2.35 + 0.73*a), -(3.23 + 1.11*a), -(2.15 + 0.85*a), -(2.45 + 1.09*a), -(3.6 + 0.4*a), 0];
lb = [0, 0, 0, 0, 0, 0, 0, 0, -inf]; ub = [];
b = [0, 0, 0, -3.12, -(4.85 - 1.03*a), -(4.95 - 0.97*a)];
linprog(f, A, b, [], [], lb, ub)
f = [0, 0, 0, 0, 0, 0, 0, 0, 1];
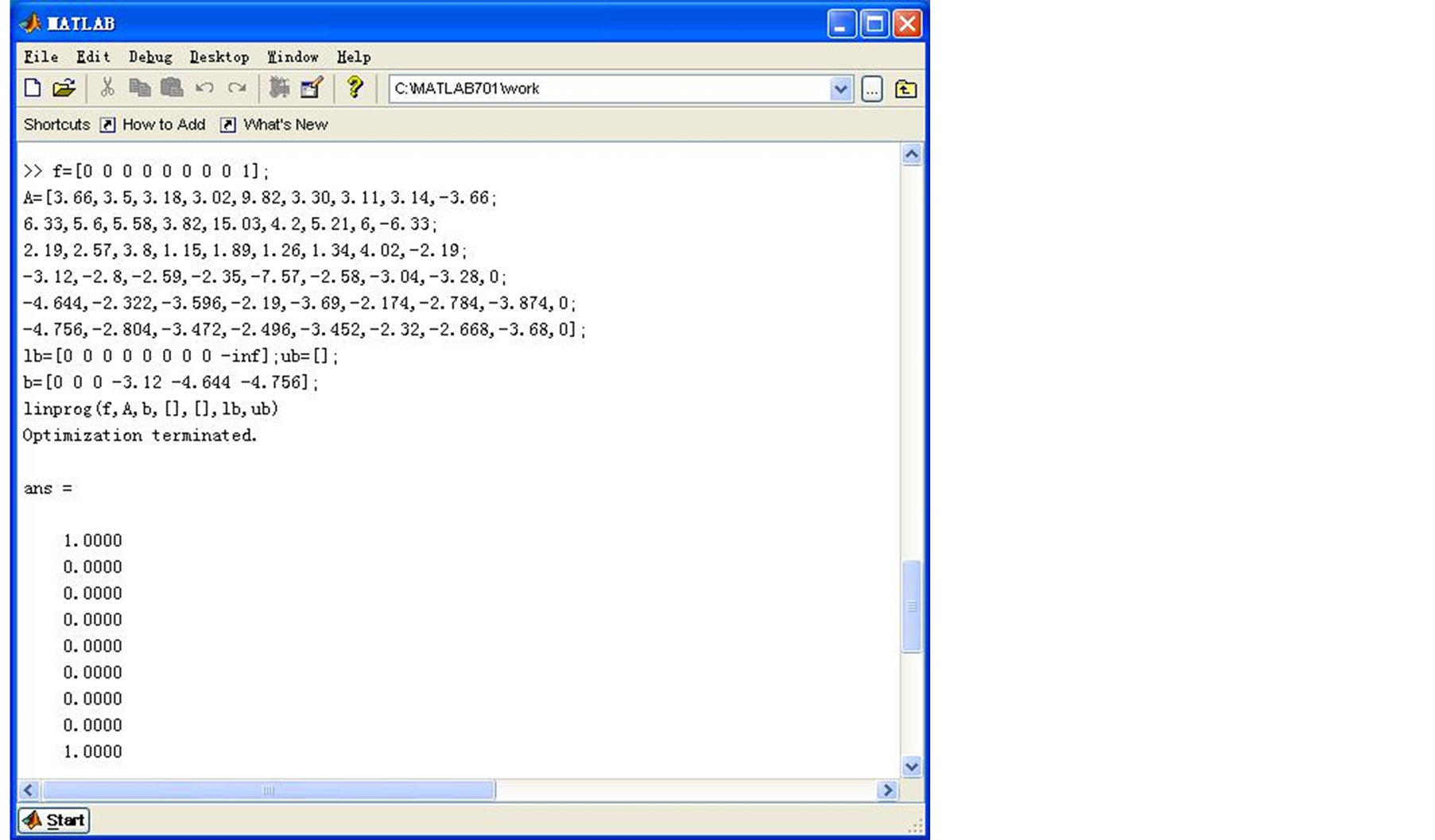
Figure 1. The calculation results by using MATLAB (1)
图1. 使用MATLAB的计算结果(1)
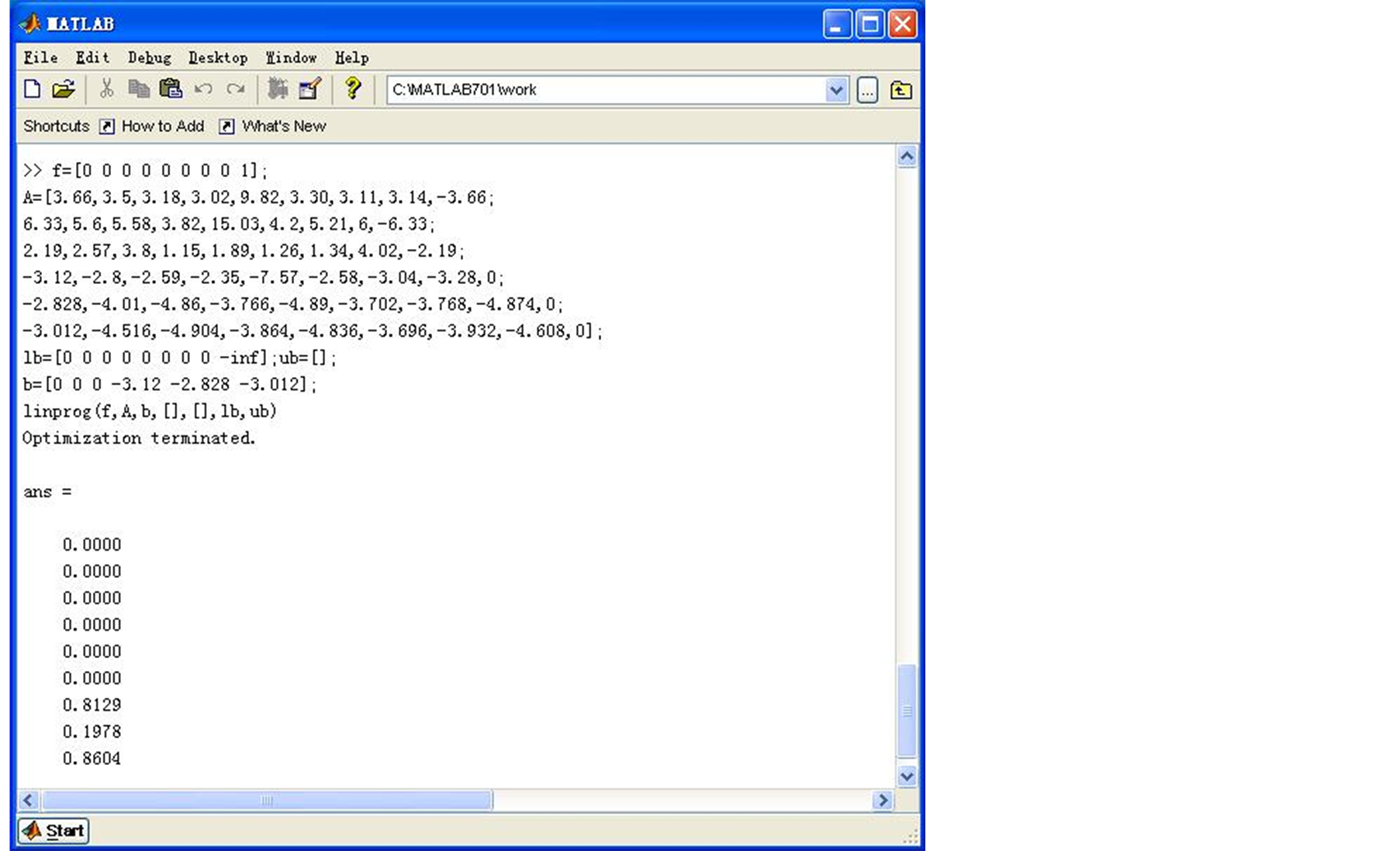
Figure 2. The calculation results by using MATLAB (2)
图2. 使用MATLAB的计算结果(2)
A = [3.66, 3.5, 3.18, 3.02, 9.82, 3.30, 3.11, 3.14, -3.66; 6.33, 5.6, 5.58, 3.82, 15.03, 4.2, 5.21, 6, -6.33; 2.19, 2.57, 3.8, 1.15, 1.89, 1.26, 1.34, 4.02, -2.19; -3.12, -2.8, -2.59, -2.35, -7.57, -2.58, -3.04, -3.28, 0; - (2.58 + 1.24*a), -(4.26 - 1.25*a), -(4.95 - 0.45*a), -(3.97 - 1.02*a), -(5 - 0.55*a), -(3.92 - 1.09*a), -(3.89 - 0.61*a), -(5 - 0.63*a), 0; -(2.77 + 1.21*a), -(4.79 - 1.37*a), -(5 - 0.48*a), -(4.06 - 0.98*a), -(4.96 - 0.62*a), -(3.87 - 0.87*a), -(4.03 - 0.49*a), -(4.76 - 0.76*a), 0];
lb = [0, 0, 0, 0, 0, 0, 0, 0, -inf]; ub = [];
b = [0, 0, 0, -3.12, -(2.58 + 1.24*a), -(2.77 + 1.21*a)];
linprog(f, A, b, [], [], lb, ub)
按照相同的方法,可以给出高职院校DMU2、DMU3、……、DMU8在置信水平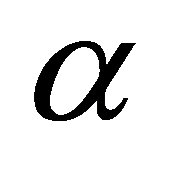 分别取0.2、0.4、0.6、0.8、1.0时的模糊DEA有效区间,最终结果如表2所示。
分别取0.2、0.4、0.6、0.8、1.0时的模糊DEA有效区间,最终结果如表2所示。
应用平均置信有效性公式,可以得到前述8所高职院校的平均置信有效值 分别为:0.927,0.893,0.979,1,1,0.999,1,1。
分别为:0.927,0.893,0.979,1,1,0.999,1,1。
据此,8所高职院校的办学效益排序为:DMU4,DMU5,DMU7,DMU8(并列);DMU6;DMU3;DMU1;DMU2。
4. 计算结果分析
依据上述结果,并对照表1中的原始数据,可以得到许多定性结论,这对于决策者提高办学效益、提升管理水平有重要价值,比如:
1) 比较两所学校DMU3和DMU4的数据就会发现,尽管其专任教师数量和毕业生人数相当,甚至DMU3的学生质量高于DMU4(可从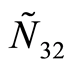 及
及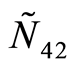 的数据看出),但DMU3的办学效益却低于DMU4。究其原因,主要是DMU3的经费投入、人员成本较高(专任教师在教职工中的比例较低);
的数据看出),但DMU3的办学效益却低于DMU4。究其原因,主要是DMU3的经费投入、人员成本较高(专任教师在教职工中的比例较低);

Table 2. Fuzzy DEA valid interval of eight Higher Vocational Colleges
表2. 八所高职院校的模糊DEA有效区间
2) 比较两所学校DMU1和DMU8的数据就会发现,尽管其专任教师数量、教职工总数、毕业生人数及质量相当,甚至DMU8的经费投入高于DMU1,但DMU8的办学效益仍高于DMU1。究其原因,主要是DMU8的优质教学成果得分明显高于DMU1(可从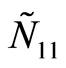 及
及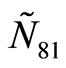 的数据看出)。
的数据看出)。
同时,对照实际情况,那些仅仅追求所谓的“大手笔”、硬件投入非常高的“豪华”学校,其办学效益往往很低。
以上这些结论表明,高职院校的办学效益本质上体现在学校的内涵建设上,如何练好高职院校的“内功”才是管理者需要认真考虑的问题。
致 谢
本文得到上海海事大学重点课程建设项目的资助,特此致谢!