1. 前言
2008年5月汶川地震、2013年5月庐山地震,给我们留下了深刻的印象,通过研究现场情况发现,威胁人们生命财产安全的首要因素就是建筑物倒塌,也就是建筑物的延性性能。同时给我们的设计者和科研人员提出了一个严峻的考验,如何保证建筑物的延性特征,如何更好的认识和了解建筑物的破坏形式,如何最大程度的避免此类事件的发生。
本文在试验的基础上提出了影响框架柱延性性能的几个特征,并得出了相应的结论,给我们的科研和设计人员提供了很好参考依据。
2. 试验方法及有线元模型的建立
2.1. 试验参数及模型的选取
本模型的北京市某住宅为设计原型,采用按比例调整,模型尺寸如下:取6 m × 6 m柱网横向为两跨的异型柱框架结构,并以轴压比较大的一榀框架为对象,底部3层,按1/3缩尺,并在第1层和第2层底部采用了带暗柱的异型柱。混凝土为C30细石混凝土,异型柱配筋采用:按照构造配筋,外包钢加固方法及试验模型如图1、图2所示。
试验加载情况:采用拟静力试验加载制度,在异形柱框架结构在边柱顶部与顶层梁交汇节点处施加低周反复水平荷载;在框架柱的顶部采用垂直千斤顶施加竖向轴力,垂直千斤顶与固定于静力台座的反力梁之间设置滚轴装置,可以保证柱顶端产生自由水平位移。试验开始时,首先在三根柱的顶部通过垂直千斤顶施加竖向轴力,其轴力为:中柱300 kN;边柱150 kN,竖向轴力一次加至指定值,试验过程中保持不变。横向力加在三层楼板位置,通过固定于反力墙上的水平拉压千斤顶对框架施加单向低周反复荷载,采用作用力和位移的混合控制加载。加载制度如图3所示。弹性阶段采用荷载控制,10 kN为一级,每级循环一次,直至达到屈服位移;弹塑性阶段采用位移控制,试件屈服后,以屈服时的水平位移Δy控制,每一级位移增加一倍Δy,每一级循环三次,直至水平荷载降至极限荷载的80%为止。
2.2. 有限元模型的建立
通过有限元分析软件ANSYS建立异性框架的有限元模型如下图4,图5所示。
3. 外包钢异性框架试验结果分析
3.1. 异性框架有限元分析[1]
计算完成后,进入ANSYS的后处理界面,利用APDL参数化设计语言编制的命令流提取位移加载

Figure 1. The schematic diagram of cladding steel reinforces special-shaped column
图1. 外包钢加固异形柱示意图

Figure 2. Effect chart reinforcement
图2. 加固效果图

Figure 3. Loading mode of the test
图3. 加载方式图
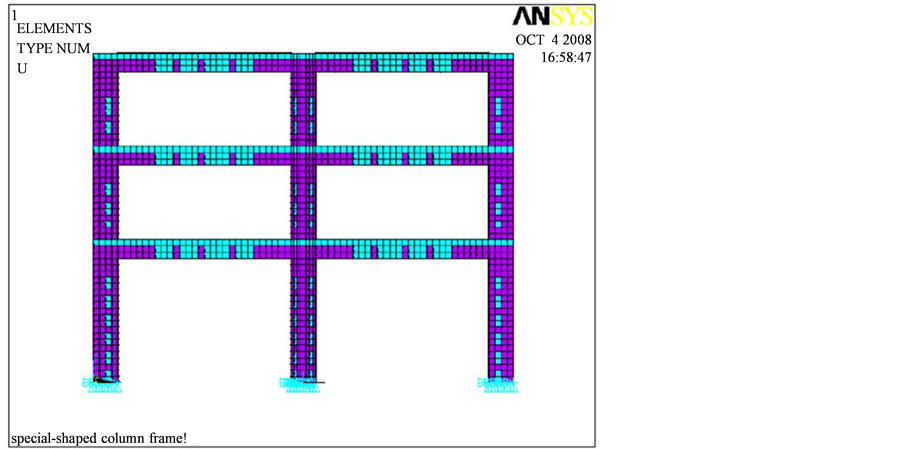
Figure 4. The mechanical model of the special-shaped column frame
图4. 异形柱框架的力学模型

Figure 5. The node of the finite element model
图5. 异形柱框架二层中柱节点的有限元模型
点的反力及柱顶位移值,即可得框架的滞回曲线。计算得到的框架滞回曲线及其骨架曲线和试验结果如图6~8所示。
在低周反复加载试验所获得的荷载—变形滞回曲线中,取所有每一级荷载第一次循环的峰值点(卸载点)所连接的包络线称作骨架曲线,它是每次循环的荷载—变形曲线到达最大峰点的轨迹。骨架曲线的形状大体上和单次加载曲线相似,但极限荷载略有降低。
由图6、图7可以发现,试验所得滞回曲线开始呈S行,而后和理论计算值比较接近,主要是由于,起始阶段外包钢和异型柱之间不能很好协调工作所造成的。由图8可以发现试验与理论所得P-△曲线比较接近,充分证明了计算模型选取的正确性。

Figure 6. The measured hysteresis curves at top-column in RC frame
图6. 框架实测的顶层P-△滞回曲线
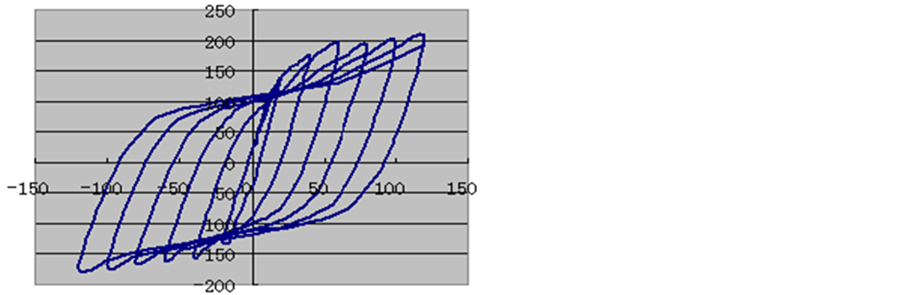
Figure 7. The theoretical hysteresis curves at top-column in RC frame
图7. 框架理论计算的顶层P-△滞回曲线
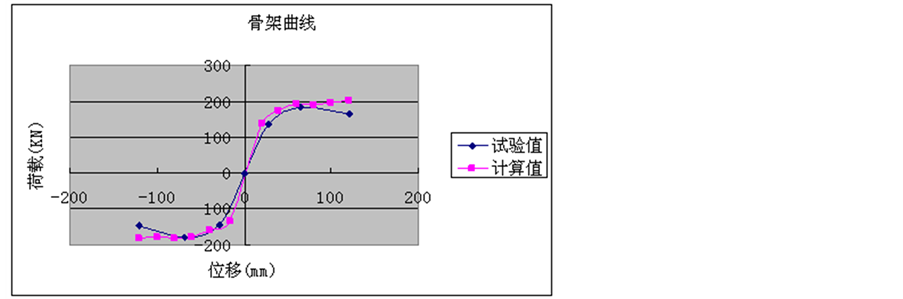
Figure 8. The comparison figure of the skeleton curves
图8. 钢筋混凝土异形柱框架实测和理论计算所得的P-△骨架曲线对比
3.2. 异性框架延性性能影响因素的有限元分析
3.2.1. 钢板厚度对延性性能的影响
采用所建立的有限元模型,变换框架柱的外包钢板厚度(分别采用3 mm,4 mm,5 mm,6 mm,7 mm,8 mm),对模型进行了分析如图9所示,由通用屈服弯矩法[2] ,算出位移延性系数,求出框架在相应钢板厚度的条件下的位移延性系数,其与钢板厚度之间的关系如图10所示。
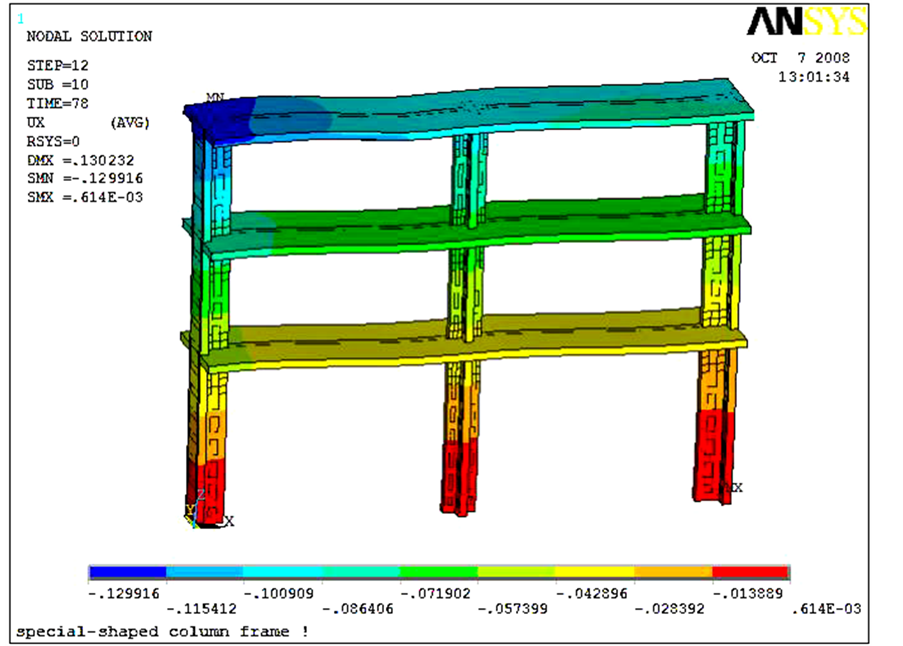
Figure 9. The plastic-hinge location (when the plate thickness is 3 mm)
图9. 塑性铰区发生位置图(钢板厚度为3 mm)
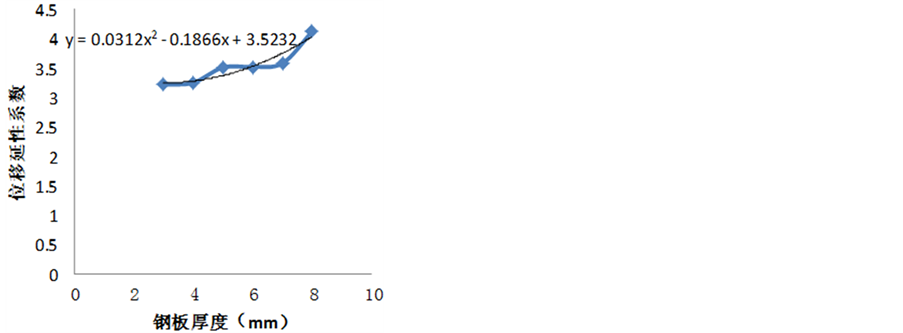
Figure 10. The relationship between displacement ductility ratio of frame and plate thickness
图10. 框架位移延性系数与钢板厚度之间的关系
3.2.2. 缀板间距对延性性能的影响
有限元模型,变换框架柱的缀板间距(间距分别取60 mm,120 mm,180 mm,240 mm,360 mm),对模型进行有限元分析如图12,由通用屈服弯矩法,算出位移延性系数,可以求出框架在相应缀板间距下的位移延性系数,其与缀板间距之间的关系[3] 如图11所示。

Figure 11. The relationship between displacement ductility ratio of frame and spacing of batten plates
图11. 框架位移延性系数与缀板间距之间的关系
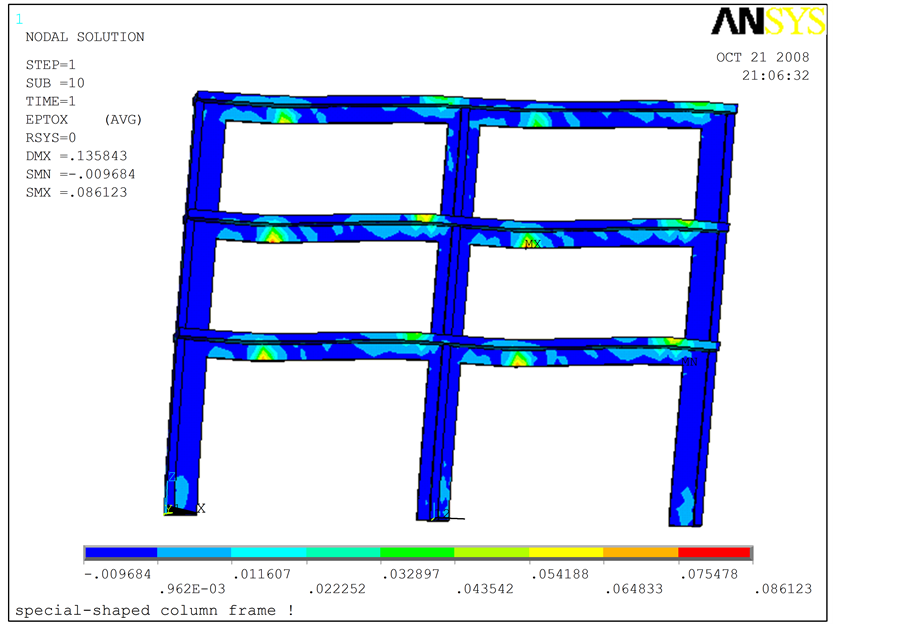
Figure 12. The plastic-hinge location (when the spacing of batten plates is 360 mm)
图12. 塑性铰区发生位置图(缀板间距为360 mm)
3.2.3. 轴压比对延性性能的影响
变换轴压比(轴压比分别为1) 边柱:0.1,中柱:0.2;2) 边柱:0.15,中柱:0.3;3) 边柱:0.2,中柱:0.4;4) 边柱:0.25,中柱:0.5;5) 边柱:0.3,中柱:0.6;6) 边柱:0.35,中柱:0.7;7) 边柱:0.4,中柱:0.8。对模型进行有限元分析如图14,由通用屈服弯矩法,算出位移延性系数,框架在相应轴压比(横坐标为边柱的轴压比,中柱轴压比为上述相应组合,以下同)下的位移延性系数[4] 如图13所示。
4. 结论
1) 由图9、图10可知,框架的延性随着框架柱的外包钢板厚度的增加而增大。当钢板厚度为3 mm时,框架的正向最大位移,塑性铰发生区域如图10所示,表明在本文所采用的加固方案下,模型仍能够

Figure 13. The relationship between displacement ductility ratio of frame and axial compression ratio
图13. 框架位移延性系数与轴压比之间的关系
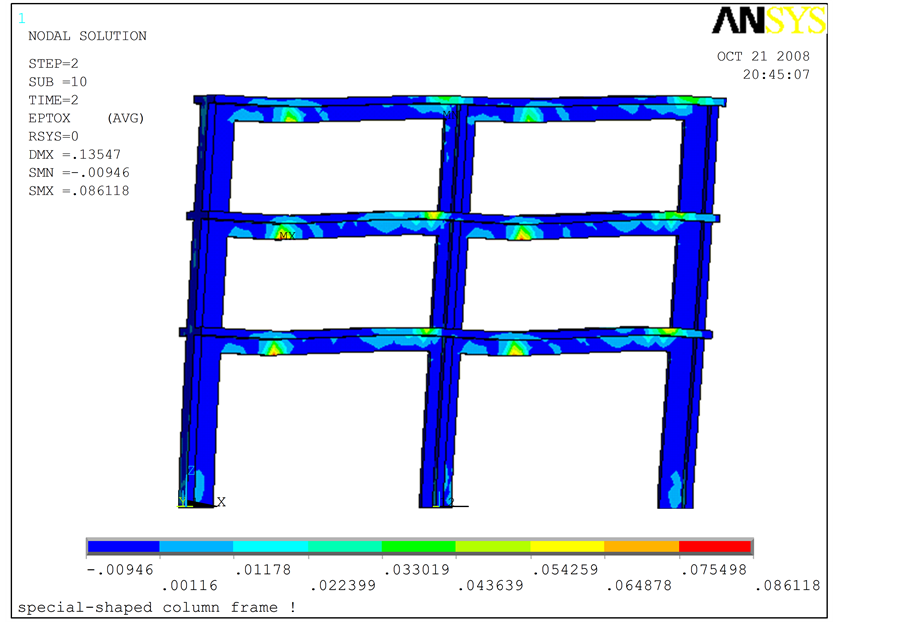
Figure 14. The plastic-hinge location (when the axial compression ratio is 0.8)
图14. 塑性铰区发生位置图(轴压比为0.8)
较好的实现梁铰延性框架机制,可以实现塑性铰向跨中转移;
通过线性回归可以发现:异性框架延性性能与加固板厚度的关系大概成线性增长,其线性关系为: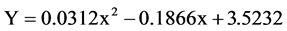 。
。
2) 由图11可知,框架的延性随着框架柱的缀板间距的增大而减小。塑性铰发生区域如图12所示,表明在本文所采用的加固方案下,模型仍热能够较好的实现梁铰延性框架机制,加固后的框架仍然为“强柱弱梁”的延性结构,可以实现塑性铰向跨中转移的设计思想;并且延性性能与缀板间距关系为: 。
。
3) 由图13可知,框架的延性随着框架轴压比的增大而减小。塑性铰发生区域如图14所示,表明在本文所采用的加固方案下,模型仍能够较好的实现梁铰延性机制;并且其延性性能与轴压比关系大致呈: 。
。
与普通矩形柱相比,异形柱构件的抗震性能较差,主要表现在其沿同一直线正反两个方向的承载力、延性差异较大,因此对轴压比更加敏感。而严格控制轴压比,将有助于减小这种延性差异,并保证异形柱构件具有较高的最低延性。异形柱框架结构的薄弱层基本出现在结构的底部一至二层。因此,应注意提高底部楼层的延性,提高其中的异形柱的延性尤为关键[5] 。
由图13可知:轴压比对截面延性有着决定性的影响。随轴压比增大,柱截面受压高度增加,极限曲率就会减小,从而截面延性下降,相应的框架延性显著下降。因此,为保证压弯构件有必要的延性,应尽量降低轴压比,如果轴压比较大,应采取一定的措施,有效的约束混凝土,配置足够的缀板以提高混凝土的极限压应变值,增加延性。因此,当被加固框架结构轴压比较小时,使用外包钢和粘钢复合加固可以保证在承载力提高的情况下,延性不会有太大降低,使之满足延性框架的要求。

NOTES
*通讯作者。