1. 引言
伴随着纳米摩擦学的发展，微/纳米粒子体在极端工况环境中的摩擦学性能引起了人们的兴趣。传统地，采用添加剂改善基础油的摩擦学性能主要是利用有机添加剂在摩擦时的微高温及机械剪切作用下会进行分解，使其在摩擦副表面形成一层保护膜，以改善其抗磨减摩效果[1] -[4] ，然而，有机添加剂在一些极压及高温等苛刻工况下依然会出现润滑失效现象。因此，在高温、高压工况环境中往往采用将某些金属或非金属超微固体粒子体添加进基础油中以制成高浓度脂类润滑剂，如：目前较为常用超微粒子添加材料主要有石墨、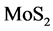
和
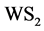等[5] -[7] 。
T. Hisakado等[8] 对粒径在30~500 nm的固体润滑油添加剂(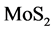
、石墨、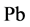
、
、
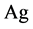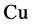等)的使用情况进行了研究，研究表明这些固体微粒在摩擦表面存在时显示了良好的极压润滑性能，且粒径越小减摩抗摩性能越好。Teterin [9] 在基础油中添加了0.1%的40~500 nm粒径
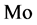粉，对比实验表明
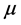值降低明显。美国Michigan大学的科研人员对常用微米固体添加剂与纳米添加剂的摩擦学性能进行的对比实验，结果表明纳米材料比传统固体润滑材料具有更出色的摩擦学性能。一些掺杂后的无机单质纳米润滑油添加剂(如
、
、
、
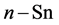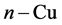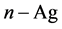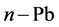等)和经改性处理各种高温化合物的纳米润滑油添加剂(如石墨、
、
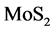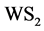等)已经有了小规模的商业应用。
上述研究工作主要是集中于润滑剂中微/纳米粒子对其摩擦学性能的改善与表面润滑膜的影响研究上，而关于微/纳米粒子润滑胶体特别是磁流润滑胶体流变性对多孔材料摩擦副间润滑影响的研究报道极少。
磁流润滑胶体作为多相胶体的一种，不考虑外磁场的作用，其在孔道中的流动过程属于典型的多相流范畴。对小孔直接进行实验数据的采集相当困难，本研究基于壁滑移机理及其对流变特性的影响，建立合适的小孔流变模型，辅以仿真分析对其流变特性进行研究。
2. 梯度流胶体柱端面形貌曲线方程
设在某一压力差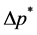
下，胶体在孔道中产生了梯度流和塞流，其塞流层端面与边壁处胶体前锋面高度差为
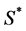，并在
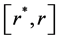内进行对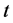
的一重积分，可求得胶体梯度区内胶体柱形貌的高度落差方程为：
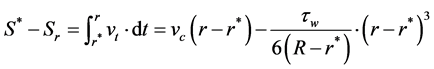
对上式移相后得到：
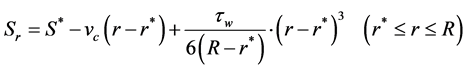(1)
上式表明，当全梯度流发生时，胶体壁面剪应力越大，孔道中的胶体前锋面越凸出。且当全梯度流发生时，最大胶体柱高度在孔道中心线处且与壁面剪应力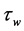
与孔道半径平方的乘积
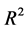成正比。
3. 梯度流层间剪切应力方程
定义孔道内壁处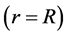
的壁面剪切应力为
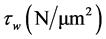，则得到了梯度区剪切应力函数的边界方程为：
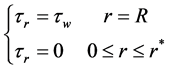(2)
由前面的讨论设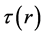
是关于半径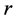
的一次函数，则由式(2)可得到
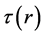的函数表达式如下：
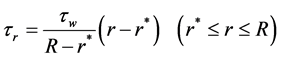(3)
其函数曲线如图1所示。
对上式进行分析：
(1) 上式表明，当孔道两端的压差足够大时，梯度流层将扩展至孔道全半径范围，此时孔道半径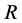
越小，胶体的流动阻力将越大。
(2) 事实上，考虑到非牛顿流体的剪切稀化和胶体在孔道中流动的摩擦热效应，此时壁面剪应力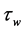
将随着流动而缓慢减小。直到胶体中的皂纤维破坏与重新生成速率、热量的生成量与扩传导散量达到新的平衡时，
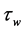才达到新的稳态值。
4. 模型验证与讨论
采用MATLAB工具可以分别仿真得到不考虑壁滑移作用时孔道半径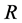
和塞流层半径
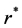对胶体平均流速
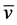的影响曲面
图2所示为不考虑壁滑移作用时孔道半径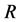
和塞流层半径
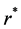对胶体平均流速
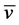的影响曲面，在本次仿真程序中胶体在孔道中流动时的修正壁面剪应力设定为
。
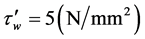由图2可知，由于在相同孔道压差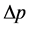
作用下胶体的粘度越大，塞流层半径
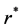越小，相应胶体在孔道中的流动速度越小；且由于没有壁滑移作用，孔道半径
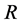越小，胶体通过孔道孔越困难。
在相同的塞流层半径下，孔道中的壁滑移层越厚，对多相润滑胶体流动性的改善作用越明显。但显然通过降低胶体的粘度来提高其在孔中的流动性是不明智的，原因在于：一方面，塞流层半径越小，意味着胶体中受剪切作用皂化纤维的比例越大，产生相漂移与组分分离的情况越严重，胶体在安定状态下所具有的流变特性、摩擦学性能、理化性有将同时发生改变；另一方面，降低胶体粘度对提高其在孔中的流动性的作用是极其有限的。
5. 本章小结
本章推导建立了相关剪应力方程、流速方程、胶体柱形貌方程和全流量方程。通过对模型方程的讨论与数值仿真分析，得到的主要结论如下：
(1) 多相润滑胶体在孔道中的非均匀剪切流动将会在孔道的内边壁附近产生一粘度显著降低的壁滑移层，而这一壁滑移层会引起胶体附加流速，从而有助于提高胶体在孔道中的流动性。
(2) 在相同的塞流层半径下，孔道中的壁滑移层越厚，对胶体流动性的改善作用越明显。但通过降低
Figure 1. Curve model
图1. 曲线坐标
胶体的粘度来提高其在孔中的流动性是不明智的，且作用有限。
(3) 当全梯度流发生时，理论上胶体的最大流速度速率将出现在孔道中心线处且最大速率仅与壁面剪应力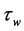
与孔道半径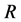
的乘积成正比。