1. 引言
由于电力系统负荷具有较强的随机性、波动性和时序性[1] [2] ,用单一负荷水平进行可靠性评估时,很难反映系统的真实可靠性水平,为此需要计入负荷曲线的影响。
在已有电力系统可靠性评估模型中,针对确定系统的分析,通常选取一个或几个典型的负荷曲线,如枯大、枯小、丰大和丰小等,进行相应的计算分析[3] -[5] 。然而不管采用多少种典型负荷类型,均是针对特定负荷曲线进行的分析研究,也没有计入各种负荷管理、调整措施的可靠性影响。如果能够采用合理的需求侧管理方法和调整措施,针对确定电量需求的电力系统,合理调整峰谷负荷的大小,显然可以改变系统的负荷率,进而改变系统的可靠性。
本文计入负荷曲线影响,结合常用的两种负荷调整策略,探讨电力系统可靠性随负荷率调整的变化规律。下面简单介绍负荷率的定义:
电力系统负荷率通常用数值或百分比表示,指在给定时间(如年、月、日等)内,系统实际用电量与假定连续使用设备的最大需求量的比值。通常,为计算方便,去除时间效应,用一天或一年中平均负荷与最大负荷的比值(或百分比)来表示负荷率。
图1给出IEEE-RTS 79测试系统[6] 年度各小时负荷曲线(已经采用最大峰值负荷归一化),系统总装
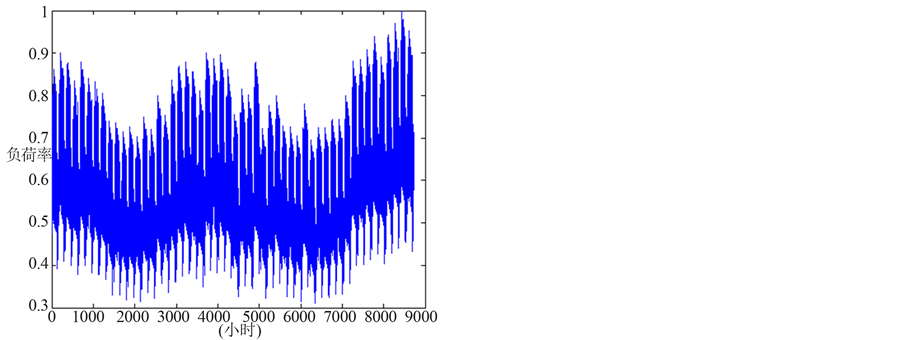
Figure 1. Annual load curve of IEEE-RTS 79 test system
图1. IEEE-RTS 79测试系统年度负荷曲线
机容量3405 MW,年最大峰荷2850 MW,年度平均负荷为1750.8 MW,负荷率为0.6143。
2. 负荷率调整策略
下面重点介绍本文提出的两种负荷率调整策略。
2.1. 削峰填谷调整策略及算法
削峰填谷是将电网高峰负荷的用电需求推移到低谷时段,同时起到削峰和填谷的双重作用。从电力系统运行角度看,它既可减少新增装机容量、充分利用闲置容量,又可平稳系统负荷、降低发电煤耗。对于电力严重短缺、负荷峰谷差距大、负荷调节能力有限的电力系统,一直把削峰填谷作为改善电网经营手段的一种重要工作。
计入负荷曲线对应的系统可靠性水平,是不同负荷水平时系统可靠性水平的期望值。为加强对比分析和提升系统可靠性,本文定义的削峰填谷策略是指:系统在确定时间段内,如:一天、一年等,在满足原负荷用电需求的情况下,合理改变负荷谷峰差,即在系统平均负荷不变的情况下合理改变系统最大负荷,以达到提高系统负荷率,进而提高系统可靠性水平的目的。
对某确定的电力系统(假设负荷曲线和负荷率已给定),下面给出基于二分法[7] -[10] 的负荷率调整策略,其包括削峰、填谷两个过程(其中,采用二分法计算的主要目的是确定新的负荷最小值,即用于填谷过程)。
基于二分法的负荷率调整算法:
1) 给定负荷数据、预调整的负荷率等;
2) 计算系统最大峰值负荷Pmax,计算原系统负荷率、最小负荷Pmin等;
3) 削峰过程:
将原负荷曲线中所有大于Pmax的负荷(集合A)修改为Pmax,形成新的负荷曲线,并记录整个过程各负荷电量改变量的总和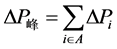 ;
;
4) 填谷过程;
4a) 计算中值负荷: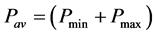 。其中,Pav表示系统平均负荷;
。其中,Pav表示系统平均负荷;
4b) 将新负荷曲线中所有小于Pav的负荷(集合B)均修改为Pav,并记录整个过程各负荷电量改变量的总和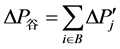 ;
;
4c) 计算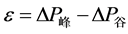 ,若
,若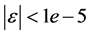 ,计算结束,此时形成的新负荷曲线即为给定负荷率负荷曲线;否则转第4d)步;
,计算结束,此时形成的新负荷曲线即为给定负荷率负荷曲线;否则转第4d)步;
4d) 若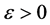 ,令
,令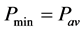 ,4a)步;若
,4a)步;若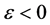 ,令
,令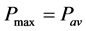 ,转第4a)步。
,转第4a)步。
对IEEE-RTS 79测试系统,其负荷率为0.6143。根据上述削峰填谷调整策略,将负荷率提高到0.7,则其对应的最大、最小负荷分别为0.8816、0.3814。经该策略调整后的新负荷曲线,如图2所示。
从图2可以看出:随着负荷率的提高,IEEE-RTS 79测试系统负荷曲线峰值负荷有所减少,低谷负荷有所提高,但其年消耗的电量保持不变。
2.2. 等比例调整策略及算法
2.1节所述的削峰填谷策略,其根本上是通过调整负荷的时间分布来达到提高负荷率的作用,其最大的特点是会改变负荷曲线的形状。本节提出一种新的负荷曲线等比例调整策略,其可以保留原负荷曲线的形状。换句话说,负荷调整过程中,负荷曲线只是经过压缩变换,二曲线的形状保持不变。
首先根据原系统负荷曲线、平均负荷和给定负荷率,计算系统峰值负荷需要调整的比例ξ:
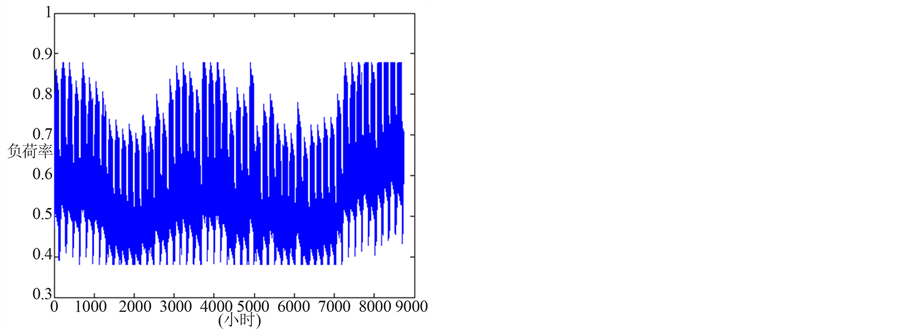
Figure 2. Changed annual load curve of the IEEE-RTS 79 using the strategy of reducing peak and filling valley (the load rate is 0.7)
图2. IEEE-RTS 79测试系统采用削峰填谷策略计算出的年度负荷曲线(负荷率为0.7)
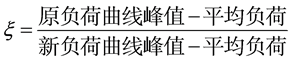 (1)
(1)
等比例调整策略是相对于平均负荷而言,即将原负荷曲线中所有大于平均负荷的部分全部缩小ξ倍;将原负荷曲线所有小于平均负荷的部分全部增加ξ倍。在时序负荷曲线图中,由于平均负荷以上的面积等于平均负荷以下的面积,因此,经等比例负荷率调整后,其负荷电量一定保持不变。
等比例调整策略算法:
1) 给定负荷数据、预调整的负荷率等;
2) 计算系统最大峰值负荷Pmax,计算原系统负荷率、平均负荷Pav和最小负荷Pmin等;
3) 计算负荷调整比例(设原系统最大负荷为1.0),则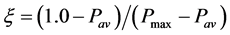 ;
;
4) 削峰过程:将原负荷曲线中所有大于Pav的负荷(集合C)按比例缩小,即: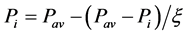 ,
,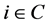 ;
;
5) 填谷过程:将原负荷曲线中所有小于Pav的负荷(集合D)按比例放大,即: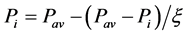 ,
,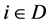 ;
;
6) 计算完成,得新负荷率下的负荷曲线。
图3给出负荷率为0.7时,IEEE-RTS 79测试系统采用等比例调整策略计算得到的负荷曲线。对比图1和图3可以看出,采用等比例调整策略计算出的负荷曲线可保留原负荷曲线的形状。
3. 可靠性随负荷率变化的三次样条插值模型
本节结合2.1节和2.2节负荷调整策略,研究电力系统可靠性随负荷率提高的变化规律。
需要指出的是,基于电力系统可靠性随负荷变化规律,结合样条插值函数[10] -[13] ,可快速估计各时段负荷对应的可靠性指标,即不需要建立多层负荷模型。然而,本文的研究重点是电力系统可靠性随负荷率的变化规律,如果一开始就采用样条插值函数估计可靠性指标,然后再用样条插值函数建立电力系统可靠性随负荷率的变化规律函数,将会使用两次插值过程,而根据误差分析理论[14] -[15] ,计算过程中过早的引入误差将对最终计算结果不利。因此,本节直接采用多级负荷模型进行可靠性评估计算,而非采用样条插值函数进行可靠性估计。三次样条插值过程如下:
设区间[a, b]有n + 1个节点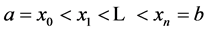 ,其对应的函数值为
,其对应的函数值为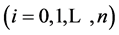
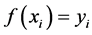 。
。
现求一定义在[a, b]上的函数S(x),使其满足:

Figure 3. Changed annual load curve of the IEEE-RTS 79 using the strategy of adjustment in equal proportion (the load rate is 0.7)
图3. IEEE-RTS 79测试系统采用等比例调整策略计算出的年度负荷曲线(负荷率为0.7)
①S(x)在每一个小区间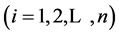
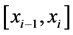 上为三次多项式;
上为三次多项式;
②S(x)在[a, b]上二阶连续可微,既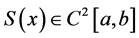 ;
;
③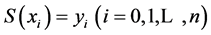 。
。
则称S(x)为f(x)的三次样条函数。
记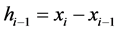 ,求S(x)的二阶导函数:
,求S(x)的二阶导函数:
 (2)
(2)
所以:
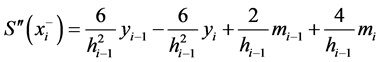 (3)
(3)
再利用S(x)在 上的表达式可计算出
上的表达式可计算出
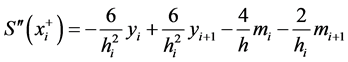 (4)
(4)
由S(x)二阶连续可微,既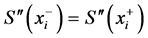 ,得
,得
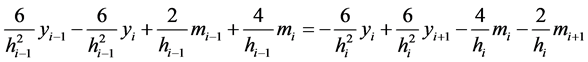
 (5)
(5)
记:
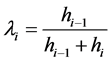 (6)
(6)
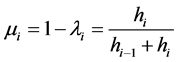 (7)
(7)
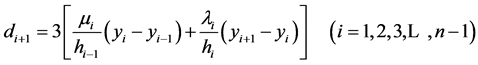 (8)
(8)
将上式整理得方程组
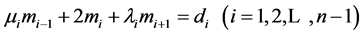 (9)
(9)
这是关于n + 1个未知量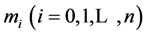 的
的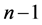 个线性方程组,该方程组有无穷多组解。在实际问题中,往往根据具体情况补充两个附加条件,即端点条件,便可唯一确定一组解,常见的端点条件有:
个线性方程组,该方程组有无穷多组解。在实际问题中,往往根据具体情况补充两个附加条件,即端点条件,便可唯一确定一组解,常见的端点条件有:
①曲线在两端点x0、x处的导数值已知,即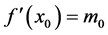 、
、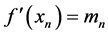 。方程组为
。方程组为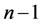 个未知数,
个未知数,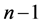 个方程,有唯一解。
个方程,有唯一解。
②函数f(x)在两端点x0、xn处的二阶导数为0,既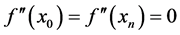 ,即:
,即:
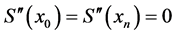 (10)
(10)
由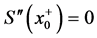 可得
可得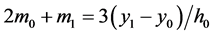 。
。
由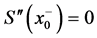 可得
可得 。
。
整理方程组
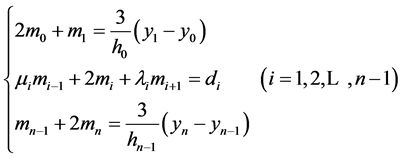 (11)
(11)
方程组也有唯一解。
③周期端点条件(当f(x0) = f(xn)):
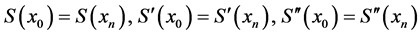 (12)
(12)
于是有:
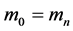 (13)
(13)
 (14)
(14)
与前面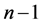 个方程联立,也可唯一求解
个方程联立,也可唯一求解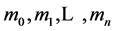 。
。
对于前面两种端点条件所对应的方程组,其矩阵形式为:
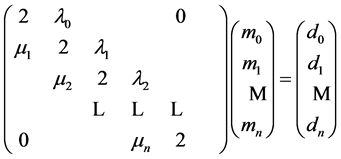 (15)
(15)
该方程组的系数矩阵具有严格对角优势(对角线元素的绝对值大于该行其他元素绝对值之和),其为非奇异阵,故方程组有唯一的解。
结合三次样条插值数学模型,设负荷率插值区间为[a¢, b¢]。假设插值区间已知n + 1个插值点,即插值区间中已知n + 1种负荷率及其对应的系统可靠性指标。设负荷率与可靠性指标变化规律函数为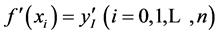 ,则可定义区间[a¢, b¢]上的三次样条插值函数S¢(x¢),其满足:
,则可定义区间[a¢, b¢]上的三次样条插值函数S¢(x¢),其满足:
①S¢(x¢)在每一个小区间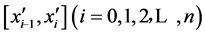 上为三次多项式;
上为三次多项式;
②S¢(x¢)在[a¢, b¢]上二阶连续可微,既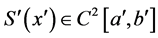 ;
;
③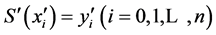 。
。
记: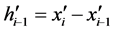
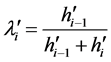 (16)
(16)
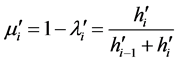 (17)
(17)
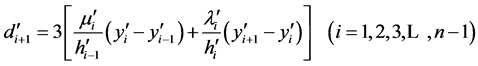 (18)
(18)
下面以发电系统LOLP指标为例,说明基于三次样条插值的系统可靠性指标随负荷率变化规律建模的步骤。其算法如下:
1) 选择边界条件,本文中均取自然边界条件,即插值区间端点处2阶导数等于0;
2) 设置插值区间[a¢, b¢]中的给定负荷率点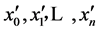 (共n + 1个),并结合削峰填谷法或等比例调整法求取给定负荷率对应的负荷曲线;
(共n + 1个),并结合削峰填谷法或等比例调整法求取给定负荷率对应的负荷曲线;
3) 基于机组追加法和多级负荷模型求取负荷率分别为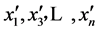 时系统对应的LOLP指标,分别为
时系统对应的LOLP指标,分别为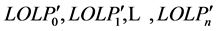 ;
;
4) 计算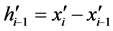 ;
;
5) 根据式(16)-(18)计算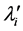 、
、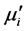 和
和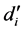 ,
,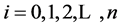 ;
;
6) 求解方程组,得到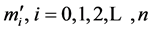 ;
;
7) 将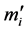 代入分段插值公式,求出各小区间
代入分段插值公式,求出各小区间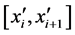 上的样条函数
上的样条函数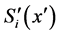 ;
;
8) 计算插值区间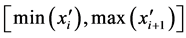 上的样条函数S¢(x¢)的值,计算结束。
上的样条函数S¢(x¢)的值,计算结束。
4. 算例分析
表1给出IEEE-RTS 79测试系统对应发电系统的可靠性评估结果。其中,负荷曲线均采用20级负荷模型。
假设负荷率分别为0.65、0.7、0.75、0.8、0.85、0.9、0.95时,表2给出了IEEE-RTS 79测试系统的LOLP、LOLF、EENS系统可靠性指标。
从表2可以看出:不管是采用削峰填谷法得到的负荷调整曲线,还是采用等比例法得到的负荷调整曲线,随着负荷率的增加,系统各类可靠性指标都有不同程度的减小,即系统可靠性水平均有不同程度的提高。
为了进一步加强对比分析,基于表2的计算结果,图4~图6给出了IEEE-RTS 79测试系统LOLP、LOLF、EENS指标随负荷率的变化规律插值曲线,插值间隔为0.01。
从图4~图6可以看出:
1) 随着负荷率的提高,测试系统可靠性得到明显改善。

Table 1. Reliability computation results of generation system of 3 test systems
表1. 三个测试系统发电系统可靠性评估结果

Table 2. Reliability indices varying with different load rates for generation system of the IEEE-RTS 79
表2. IEEE-RTS 79发电系统主要可靠性指标随负荷率变化规律
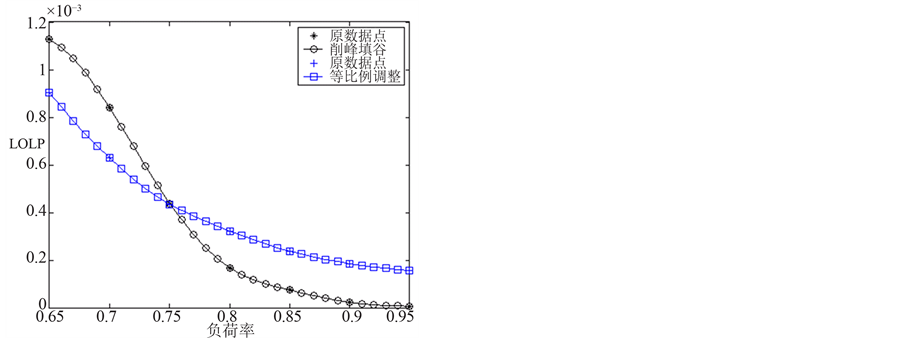
Figure 4. Curves of LOLP indices varying with different load rates for the generation system of the IEEE-RTS 79
图4. IEEE-RTS 79发电系统LOLP指标随负荷率的变化规律
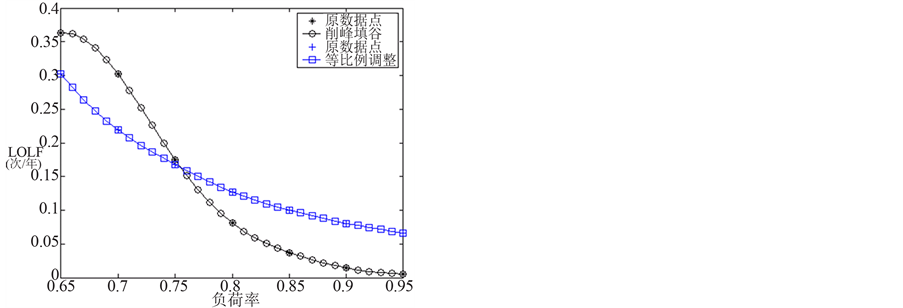
Figure 5. Curves of LOLF indices varying with different load rates for the generation system of the IEEE-RTS 79
图5. IEEE-RTS 79发电系统LOLF指标随负荷率的变化规律
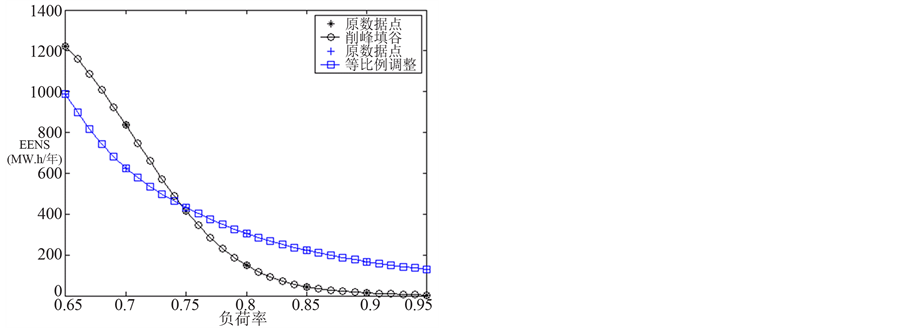
Figure 6. Curves of EENS indices varying with different load rates for the generation system of the IEEE-RTS 79
图6. IEEE-RTS 79发电系统EENS指标随负荷率的变化规律
2) 对系统可靠性指标而言,随着负荷率的增大,采用削峰填谷法和采用等比例法得到的系统可靠性对负荷率变化曲线均有交叉:交叉前等比例调整法得到的负荷曲线对应的可靠性相对较好,交叉后削峰填谷法得到的负荷曲线相对较好。这主要是因为:负荷率刚开始增加时,此时系统可靠性指标主要由峰值间段决定,由于等比例变化是对峰值负荷整体等比例缩小,所以改善效果较好;由于等比例削减是整条负荷曲线相对应平均负荷的等比例增大或减小,单个小时负荷曲线间的大小比例并没有得到实质性改善,即负荷曲线波动性仍然存在;对于削峰填谷负荷削减策略而言,开始时只有部分峰值负荷被转移到低谷负荷,系统可靠性改善有限,但随着负荷率的增加,大部分峰值负荷均被转移到低谷负荷,负荷曲线波动性得到明显改善,所以在平均负荷不变的情况下,与等比例调整方法相比,削峰填谷策略后期优势更为明显。
5. 结论
本文首先给出削峰填谷、等比例调整两种负荷率调整方法的基本原理和求解算法,并基于三次样条插值函数,给出系统可靠性随负荷率的变化规律建模思路。
采用IEEE-RTS 79测试系统进行算例分析,研究负荷率调整对系统可靠性的影响规律。算例分析表明:1) 对测试系统而言,随着负荷率的提高,不管是发电系统可靠性还是发输电组合系统可靠性,均得到不同程度的提升,但系统可靠性的提升并非呈线性变化;2) 相同负荷率下,削峰填谷法和等比例调整法得到的系统可靠性水平不尽相同,但二者对应的可靠性随负荷率的变化规律曲线均有交叉。