1. 引言
火星探测计划是中国航天工程中,继发射人造地球卫星、载人航天、探月工程之后的第四大领域,尤其是2011年11月9日,搭载中国的火星探测器“萤火一号”的俄罗斯的“福布斯–土壤”火星探测器任务失败,以及在2013年11月5日,印度成功发射了首枚火星探测器,都深深地影响了我国的火星探测计划,促使我国必须大力发展以火星探测为基础的深空探测活动[1] 。
火星作为太阳系中的行星,包括轨道高度、半径、质量、自转周期等各个特征都与地球极为相近,可以把火星和地球比作孪生兄弟。对火星进行探测,对我国乃至整个人类的深空探测活动都有着深远的意义。自1962年11月苏联发射“火星1号”探测器到如今,人类已经发射了超过40颗火星探测器,其中成功率接近50%,目前,包括好奇号在内的7个探测器仍然在火星及轨道工作。
在地球–火星往返轨道优化设计中,全世界通常采用的是基于二体动力学模型的能量等高线图,通过霍曼转移和有时间拘束的兰伯特问题的求解,进行圆锥曲线拼接,由此完成航天器整个地球–火星往返轨道的设计[2] 。然而,在地球–火星往返轨迹的设计中,通常可选的优化方案很多,寻找全局最优轨迹设计是核心问题[3] 。
本文从我国的火星任务发出,从我国的海南发射场发射一颗火星探测器,采用了一种静态参数优化与动态参数优化的全局一体化的火星探测轨迹组合优化算法进行轨迹设计[4] 。静态参数优化方法采用了全局搜索法;动态参数优化方法采用改进的动态规划法和共轭梯度法。首先,利用动态规划法和静态参数优化在任务时间内,搜索最优的发射窗口和返回窗口,并使航天器所需能量最小;同时,获得了一个次优方案;然后利用共轭梯度法来求解该两点边值问题,获得最优方案。通过长时间大规模数值仿真,验证了该组合优化算法是可行的,现详细介绍如下。
2. 问题描述
航天器地球–火星往返轨迹问题描述如下:
航天器的初始质量为m0 = 1500 kg,结构质量为md = 500 kg,燃料质量为1000 kg;推进器的比冲为Isp = 3000 s,推进的速度方向可以任意设定,推进器的开关时间和次数没有限制。航天器出发时间为MJD = 57112~57843 (2015年4月1日与2017年4月1日之间),在火星执行任务1至2年时间,然后返回地球。
优选发射窗口t0和初始速度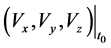 ,即需要优化静态参数
,即需要优化静态参数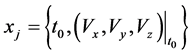 ,使得满足以下性能指标
,使得满足以下性能指标
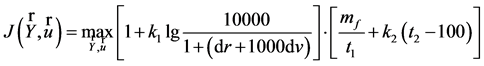 (1)
(1)
取最小,式中,mf为航天器返回地球时的剩余质量(kg);dr为航天器与火星交会时的位置误差(米);dv为航天器与火星交会时的速度误差(米/秒);k1 = 0.10,k2 = 0.02为指标加权系数;t1为任务飞行时间,即航天器从地球出发到火星+从火星出发返回到地球的飞行时间(天):
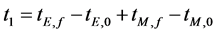 (2)
(2)
式中tE,0,tE,f,tM,0,tM,f分别是航天器离开地球的时间,到达火星的时间,离开火星的时间,到达地球的时间;t2为航天器在火星停留的时间(天):
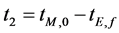 (3)
(3)
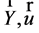 分别是需要优化的静态与动态参数:
分别是需要优化的静态与动态参数:
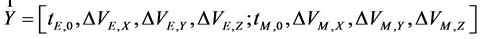 (4)
(4)
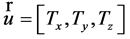 (5)
(5)
并满足以下约束条件:
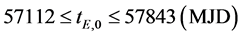 (6)
(6)
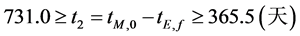 (7)
(7)
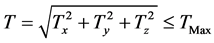 (8)
(8)
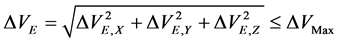 (9)
(9)
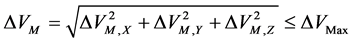 (10)
(10)
飞行器最大可用推力: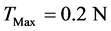 ;飞行器离开行星时的最大可用速度差:
;飞行器离开行星时的最大可用速度差: ,并且离开地球与离开火星时分别与这两颗行星的相对速度
,并且离开地球与离开火星时分别与这两颗行星的相对速度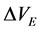 与
与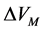 的获取而需的加速度所耗燃料,本问题中不作兼顾考虑,由其它子系统提供。
的获取而需的加速度所耗燃料,本问题中不作兼顾考虑,由其它子系统提供。
由(1)式可得,要使得性能指标最大,航天器与火星交会时的误差(dr,dv)最小,航天器返回地球时的剩余质量mf最大,任务飞行时间t1最短,同时航天器留在火星探测的时间t2最长。
地球和火星绕太阳运行采用多体动力学模型,详见文献[5] 。
3. 轨迹优化方法
关于组合优化算法,详见文献[6] 。
4. 仿真结果及分析
在J2000太阳坐标系中,探测器于tE,0 = 57429.628 (MJD)时刻从地球出发,飞离地球时,与地球的位置与速度为表1;探测器与火星相遇时刻为tE,f = 57664.968 (MJD),与火星的位置与速度为表2,此时探测器剩余质量为1221.8971 kg;探测器从火星出发返回地球的时刻为tM,0 = 58164.863 (MJD),飞行器与火星的位置与速度为表3;探测器到达地球的时间为tM,f = 58385.769 (MJD),探测器与地球的位置与速度为表4。

Table 1. The position (km) and velocity (km/sec) of detector from Earth
表1. 探测器从地球出发时的位置(km)和速度(km/sec)

Table 2. The position (km) and velocity (km/sec) of detector when arriving Mars
表2. 探测器达到火星时的位置(km)和速度(km/sec)

Table 3. The position (km) and velocity (km/sec) of detector from Mars
表3. 探测器从火星出发时的位置(km)和速度(km/sec)

Table 4. The position (km) and velocity (km/sec) of detector when arriving Earth
表4. 探测器达到地球时的位置(km)和速度(km/sec)
4.1. 地球–火星轨迹:
探测器从地球出发到达火星的最优4-D飞行轨迹、速度~飞行时间、推力控制~飞行时间、飞行器质量~飞行时间分别见图1~图4。
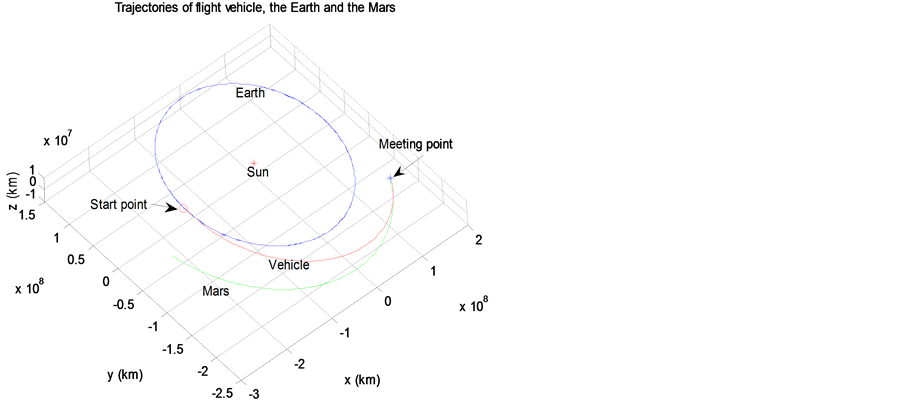
Figure 1. The optimal flight trajectory from Mars to earth
图1. 从地球到火星的最优飞行轨迹
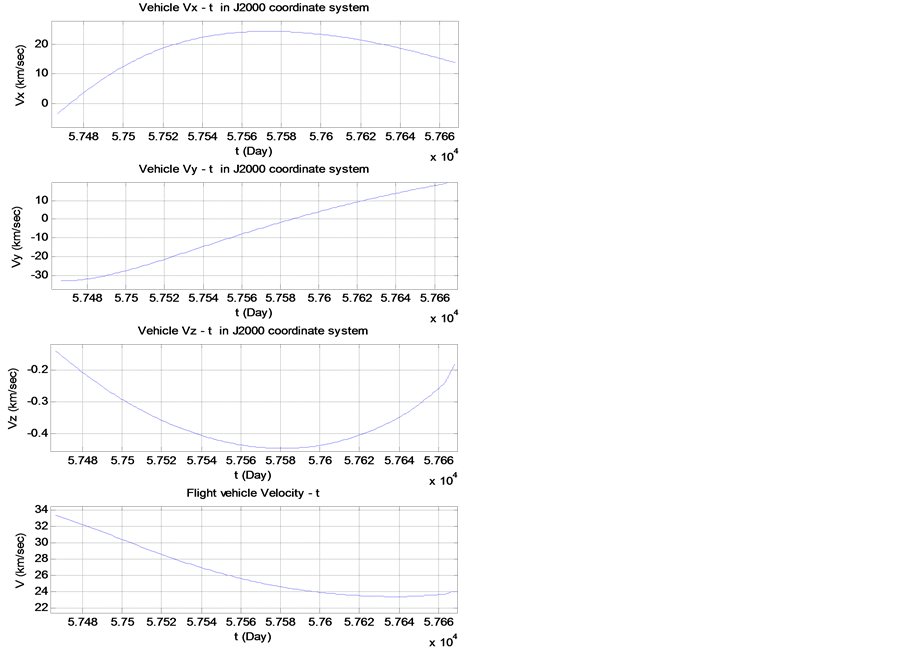
Figure 2. The velocity changes with time at starting
图2. 出发时速度随时间的变化
4.2. 火星–地球轨迹
飞行器从火星返回地球的最优4-D飞行轨迹、速度~飞行时间、推力控制~飞行时间、飞行器质量~飞行时间分别见图5~图8。
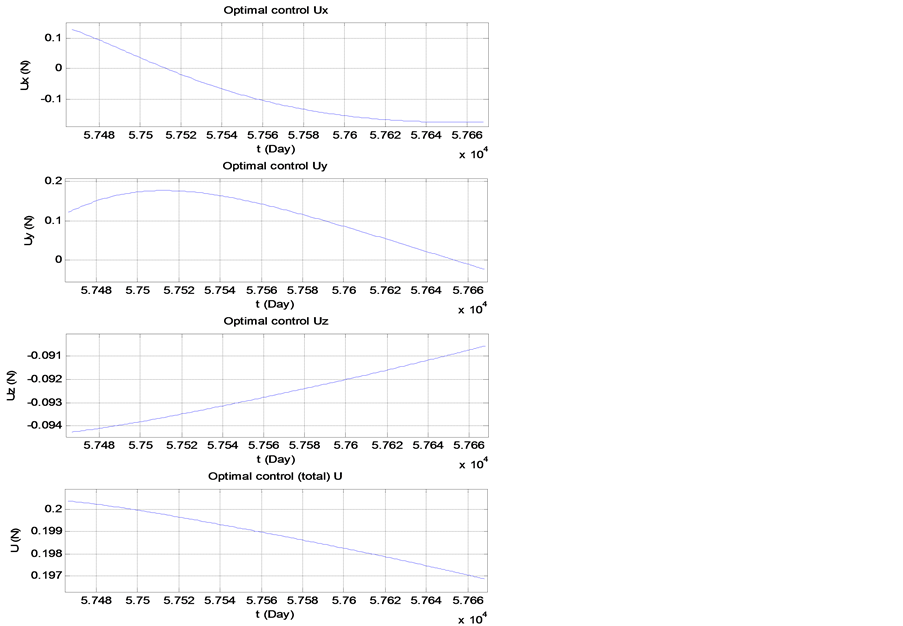
Figure 3. Change of control volume with time
图3. 出发时控制量随时间的变化
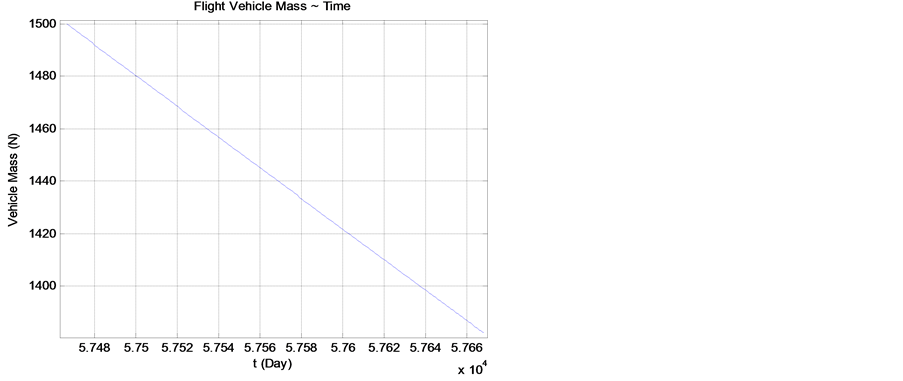
Figure 4. The change of mass with flight time
图4. 质量随飞行时间的变化
4.3. 仿真结果分析:
(1) 由仿真结果可以得到:
全部往返飞行时间为
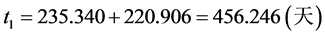
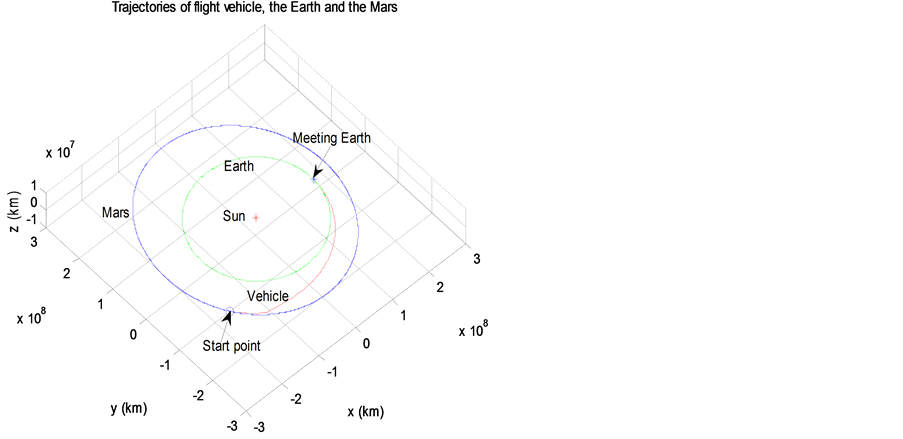
Figure 5. The optimal flight trajectory of detector from Mars to the earth
图5. 探测器从火星到地球的最优飞行轨迹
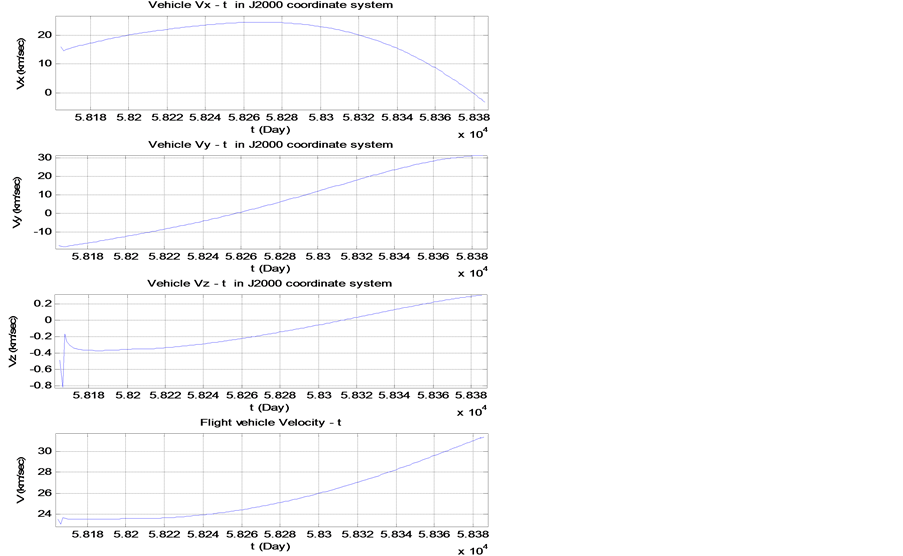
Figure 6. The changes of the velocity with time when returning
图6. 返回时速度随时间的变化
飞行器在火星上探测时间为:
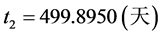
(2) 满足控制变量约束
从图3和图7可以看出,整个飞行任务过程中控制变量U小于0.2 N。
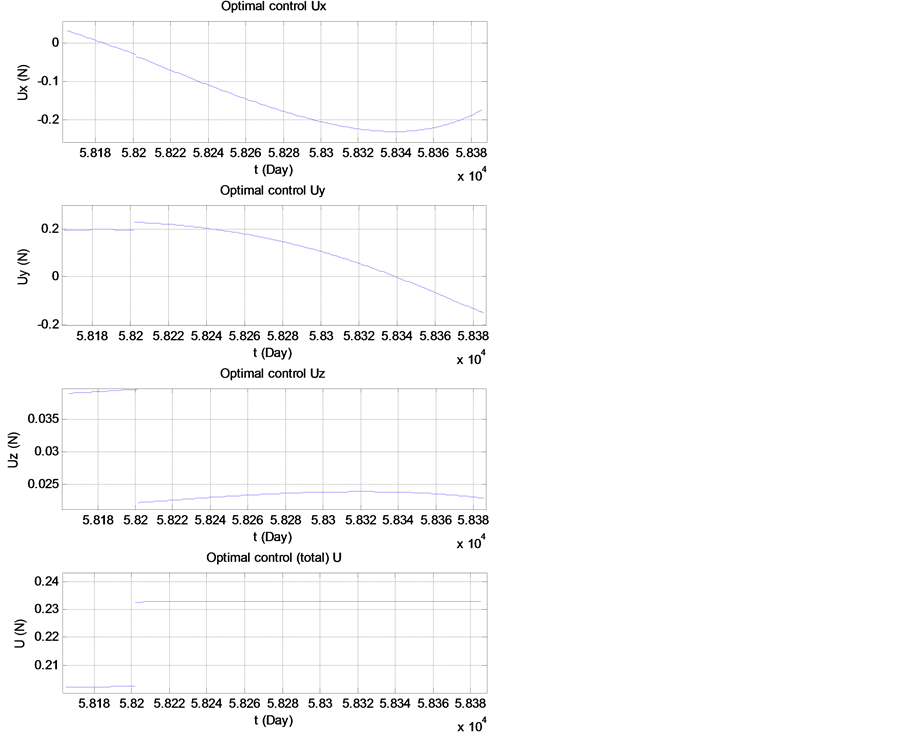
Figure 7. Change of control volume with time when returning
图7. 返回时控制量随时间的变化
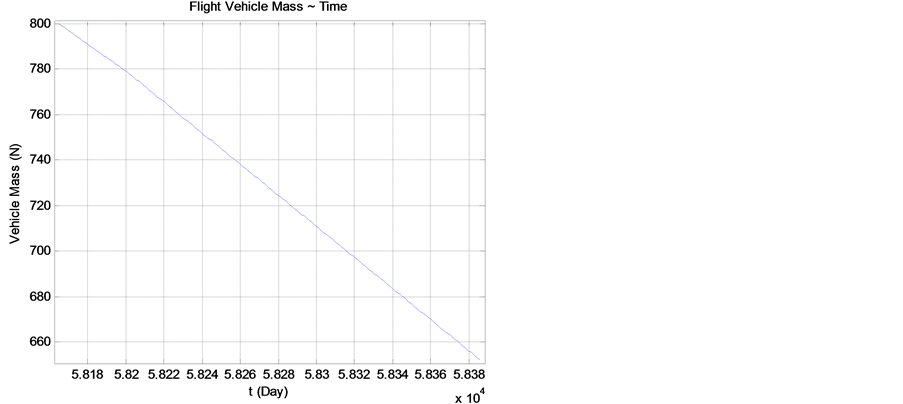
Figure 8. Quality change with time
图8. 质量随时间的变化
(3) 燃料消耗量
从图4和图8可以看出,探测器在整个飞行任务燃料消耗了850 kg,其中包括地球飞往火星消耗的燃料和从火星探测期间后返回地球飞行所消耗的燃料。
5. 结论
针对探测器在地球与火星之间的往返飞行轨迹的全局一体化优化设计问题,本文采用了一种航天器轨迹优化的组合算法,该算法是在各种约束条件下,静态参数优化+动态优化相互迭代的数值优化算法。经过大规模的数值仿真,得到了在地球与火星之间的最优往返飞行轨迹,该飞行数值仿真结果表明,该轨迹优化的数值仿真算法对航天器轨迹优化具有良好的通用性,具有明显的工程实用价值。