1. 引言
导线舞动是指高线电线在风的激励作用下的震荡运动，从某一小段导线看来，这种舞动可能同时存在相对于地球绝对坐标系的三维空间的扭转和平动。由于高压电线一旦舞动起来，其时间可能长达几个小时，以200米档距的来看，其单点的舞动幅值可能达到十几米，这种舞动对电网会造成严重的损害。因此我国研究人员早在五十年代就提出对导线舞动进行预防和治理措施[1] 。预防主要是对导线进行实时监测，由于高压电线和杆塔一般建在旷野或者山上，人员相对稀少，所以监测主要是依靠远程技术手段。现有的监测技术有视频监测和基于传感器的舞动轨迹监测。传统的基于加速度传感器的导线舞动检测技术能够提供测量点的加速度信息，经过计算之后可以得到测量点的位移。目前的加速度传感器是基于微机电技术，其优点是价格便宜，噪声小，容易集成到电路板上，封装容易，长时间使用性能可靠，其缺点是加速度计读数的变化并不一定是由于加速度造成的，扭转同样可以改变加速度计的读数，这就会带来一个问题，当测量点同时有比较大的扭转又有平动加速度时，仅仅从加速度计的读数无法区分扭转和平移分量。传统的仅仅基于加速度计的算法把测量点假设成一个质点，直接忽略舞动中的扭转，其位移估算结果很难保证正确性。
本文主要研究用传感器监测导线舞动的技术和方法。鉴于仅仅依靠加速度计测量导线舞动中存在的问题，本文提出用九轴传感器(九轴传感器包括三轴加速度计，三轴磁力计，三轴陀螺仪)测量导线舞动的方法。即应用现有的姿态估计算法(attitude estimation，本文中对姿态和扭转不加区分)，用三轴磁力计加上三轴陀螺仪组成的六轴传感器来估计舞动中的扭转，用三轴加速度计在扭转已经估计出来的基础上，对舞动过程中的平移加速度进行估计，进而通过二次积分得到平动位移。从而区别于传统监测技术(仅仅使用加速度传感器得到测量点的平动位移)，得到监测点的完全的舞动信息。
2. 导线舞动算法合理化约束和假设
本文中导线单点舞动为在受限制三维空间内可能同时存在相对地球绝对坐标系的测量点的扭转和平动，并且假设扭转和平动这两种运动形式相互独立。测量点的平动是指测量点在监测过程中自身坐标轴(body frame)相对于地球绝对坐标系(inertial frame) [2] 仅有平移而无转动，其位移可以等效为坐标系原点的位移，如图1(a)。而扭转则是有相对转动，如图1(b)中仅有扭转而无平动；图1(c)中则同时存在这两种运动。
由其定义不难得出如下公式：
(a) (b) (c)
Figure 1. Translation and reversion sketch map
图1. 平动和扭转示意图
1) 位移
(1)
其中
属于
，是三维向量，代表测量点在
时刻(时间起点从开始监测算法)相对于地球绝对坐标系(inertial frame)的位移。
2) 扭转角
(2)
其中
属于
代表测量点在
时刻(时间起点从开始监测算起)相对于地球绝对坐标系(inertial frame)的角位移。
我们除上述这两个约束(运动空间局限在一定范围内和导线测量点实际运动的位移和角位移都是有限值)之外，考虑到算法开发的复杂性和传感器组合的灵活性，我们给出如下合理化假设：我们使用的三种类型的三轴传感器，每个传感器的三轴之间是相互独立的，在不同的舞动形式下缺乏普遍的数学联系。因此测量点舞动监测算法应该是面向三维空间的，对运动空间维度进行限制(例如把三维降为二维，同时有一个轴得到的数据就完全噪声化，对其他两轴没有任何辅助作用)并不能使问题变得有丝毫简单。
3. 九轴算法架构论述
3.1. 九轴算法和传统算法的比较
在实际应用中，传感器测量装置总是和测量点固定在一起，随着测量点导线的舞动而一起舞动。假设测量装置与测量段导线在舞动过程中不发生相对运动。我们把测量点处一小段导线相对于地球绝对坐标系的运动分解为平动和扭转两种运动形式，若在
时刻(从开始测量算起)平动加速度为
，扭转为
则在不考虑向心加速度[3] 的情况下，加速度计的读数为
如式(3)，
为重力加速度，
为加速度计噪声。
为舞动中测量点的扭转。由公式可以看出，加速度计的读数并不单纯是平动加速度的函数，还和扭转相关。传统的只用加速度计的算法认为简单地忽略
，即认为实际平动加速度为
如式(4)。
(3)
(4)
我们举例说明传统算法可能导致的错误。如图2中，假设初始时传感器坐标(舞动监测点坐标)与地球
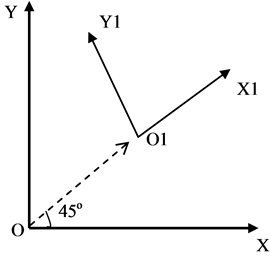
Figure 2. Reversion of measuring point lead to the inconformity of accelerate reading and true value
图2. 测量点的扭转导致加速度计读数与真实值不一致
绝对坐标系方位相同，都为OXYZ(Z轴垂直纸面向里)，测量点相对绝对坐标系的平动加速度为
，并且保持不变，则初始加速度计的读数为
如式(5)；由读数得到测量的平动加速度为：
，如式(6)。而当在
时刻，传感器随测量点绕Z轴逆时针转动45˚之后，虽然平动加速度仍为
，但此时加速度计的读数为
如式(7)；进而由读数得到测量的平动加速度为
如式(8)。显然在有扭转的情况下，仅用加速度计无法得到真实的平动加速度。
(5)
(6)
(7)
(8)
而九轴算法先通过六轴传感器得到姿态四元数，并将其转换为旋转矩阵，算出对
的估计值
，进而得到平动加速度为
如式(9)，
为九轴算法对平动加速度的估计噪声。在这个例子中，
我们可以看到，用九轴架构得到的平动加速度为真实值加上估计噪声。估计噪声的水平反应九轴架构的精度，取决于陀螺仪和磁力计以及加速度计本身的噪声水平以及六轴姿态估计算法的可靠程度，并且与实际平动加速度有关。我们可以通过降低传感器本身的测量噪声以及开发更可靠的算法来提高九轴架构对真实平动加速度的还原能力。我们将先介绍六轴姿态估计算法，之后用仿真实验证明，即使存在估计噪声，相比于传统算法，短时间内九轴架构仍能比较准确地还原舞动轨迹。
(9)
3.2. 六轴姿态估计算法
Sebastian O.H. Madgwick 2011年提出基于九轴和六轴传感器的姿态估计算法[4] ，其核心思想是将用加速度计和磁力计通过梯度下降法得到的姿态四元数，与由陀螺仪积分得到的姿态，进行线性融合，得到最优的姿态。由于我们的应用中只能使用磁力计和陀螺仪估计姿态，我们将其六轴IMU算法目标函数修改为
，如式(10)，其中：
。符号
代表四元数乘法(quaternion product)，
为传感器坐标系相对于地球绝对坐标系的单位姿态四元数，
为其共轭，
表示单位化的地磁场向量，
为校正后的单位化的磁力计读数。则由磁力计基于梯度下降法得到的姿态四元数为
如式(11)，其中：
。同时由陀螺仪估计得到的四元数为
如式(12)，其中：
为陀螺仪读数，
为采样时间间隔。融合部分的我们仍采用Sebastian 论文中的方法，最后得到的姿态四元数为
如式(13)，其中参数
需要根据传感器噪声水平通过实验进行确定。磁力计使用前，要进行校正，估算出硬铁和软铁矩阵[5] 。得到四元数之后可以通过公式转换成旋转矩阵。六轴扭转估计算法流程图如图3。
(10)
(11)
(12)
(13)
3.3. 速度与位移公式
得到平动加速度之后，进行二次积分，可以得到平动位移，如式(14)、(15)。由于实际数据时从传感器中采集的离散信号，所以将上述公式进行离散化得到迭代的计算公式，如式(16)、(17)，其中：
为采样时间间隔。
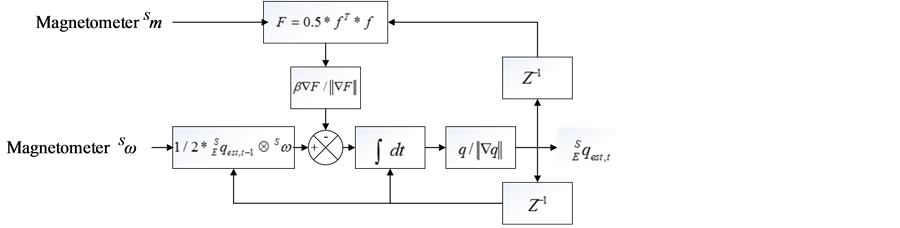
Figure 3. Six-axis reverse estimation algorithm flow chat
图3. 六轴扭转估计算法流程图
(14)
(15)
(16)
(17)
4. 实验
我们首先进行二维平面上的仿真模拟舞动实验，然后依据之前传感器各轴相互独立的假设，将结论推广到三维。
仿真实验：
因为缺乏试验系统记录测量点的扭转，我们借助MATLAB平台进行实验仿真，对比传统算法和九轴算法在舞动中存在较大扭转时的监测准确度，因为只有加速度计无法得到扭转，所以我们仅仅比较两种算法得到的平动位移的精确度。
我们使用论文[6] 中的误差分析建模传感器读数，分别为：
(18)
(19)
(20)
式中：na、nm、
均由三部分(即固定偏差、白噪声序列和不稳定偏差序列)组成。
仿真模拟的舞动位移数值为
如式(21)，波形图如图4。扭转欧拉角为
。仿真中初试位移
，初试速度
，初试扭转角
均为零。传统算法计算流程如图5，九轴算法计算流程如图6。
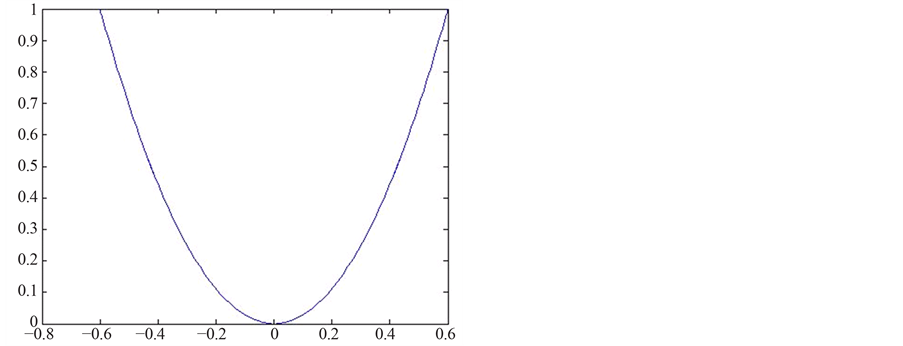
Figure 4. Simulation wave displacement (YZ plan)
图4. 仿真舞动位移(YZ平面)
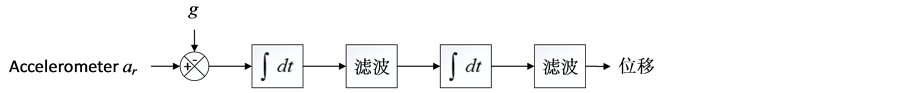
Figure 5. Traditional algorithm restoring flow chat
图5. 传统算法还原流程图
(21)
结果对比：只用加速度还原的运动轨迹如图7；用九轴还原的轨迹如图8。Maxangle取0度，30度，45度，60度，90度，120度。图中红线为真实轨迹。仿真时间T = 60秒，采样频率50 hz。
5. 总结
本文提出导线舞动监测的九轴架构，从算法理论和实验上证明了在存在比较明显的扭转时，九轴算法相比于传统算法在还原准确度上存在巨大优势，应该是后续基于微机电传感器的舞动监测的研究方向。我们仍应注意到，九轴架构在导线舞动监测上仍存在很多问题，例如陀螺仪、加速度计的积分初值难以确定，积分结果的随机游走等。我们将在后续的工作中予以进一步研究和探索。
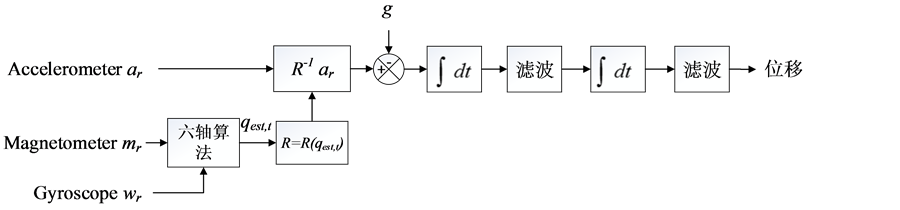
Figure 6. Nine-axis calculation restoring flow chat
图6. 九轴算法还原流程图
(a) (b) (c)
(d) (e) (f)
Figure 7. Contrast of traditional calculating displacement and true value
图7. 传统算法位移与真实值对比((a)、(b)、(c)、(d)、(e)、(f)依次为0、30、45、60、90、120度)
(a) (b) (c)
(d) (e) (f)
Figure 8. Contrast of nine-axis calculating displacement and true value
图8. 九轴算法位移与真实值对比((a)、(b)、(c)、(d)、(e)、(f)依次为0、30、45、60、90、120度)