1. 引言
内循环三相流化床具有结构简单、混合良好、能耗较低等优点,已被广泛应用在石油化工、印染工业、食品加工等领域的废水处理过程中[1] [2] 。但由于多相流过程的复杂性及多相流测量方法和成本的限制,现阶段的研究多集中于反应器中全床平均流体力学规律[3] [4] ,对各局部流体力学参数和相含率的轴径向分布的研究非常有限。近年来,随着计算机技术、数理方法和流体力学理论的发展,基于计算流体力学(Computational Fluid Dynamic, CFD)的数值模拟在反应器流场的研究中运用越来越多[5] -[7] 。相比于实验研究,数值模拟方法成本低、速度快。同时,模拟结果既可以得到反应器中的总体流动参数,又可以分析反应器中的局部流动特征。在掌握反应器内流动特性,优化反应器结构的分析设计中,利用计算机进行数值模拟是一种重要的研究手段。
本文基于CFD技术,利用Fluent商用软件对内循环三相流化床进行数值模拟。对反应器内局部的气、固相含率以及液相速度的轴径向分布规律进行分析。加深了对内循环三相流化床内部流场的认识,为内循环三相流化床的开发和设计提供参考。
2. 模型建立
2.1. 物理模型和网格的划分
内循环三相反应器主要尺寸如图1所示,反应器液面高度H = 980 mm,循环段高度Hd = 665 mm,反应器内径D = 105 mm,导流洞内径d = 70 mm,导流筒厚度为δ = 5 mm,底隙高度h = 20 mm。反应器主要分为顶部分离区、中部循环区、底部布气区。气相由底部气体分布器进入反应器,大量气泡通过升流段向上到达气液分离区逸出,少量气泡由液相带入降流段参与循环。升、降流段气含率形成压力差,推动液相和载体循环流动。
气、液相分别为标准状态下的空气、水,固相为人工高分子材料其密度为1320 kg/m3,直径为0.5~1 mm,反应器中固含率为总体积的2.5%。
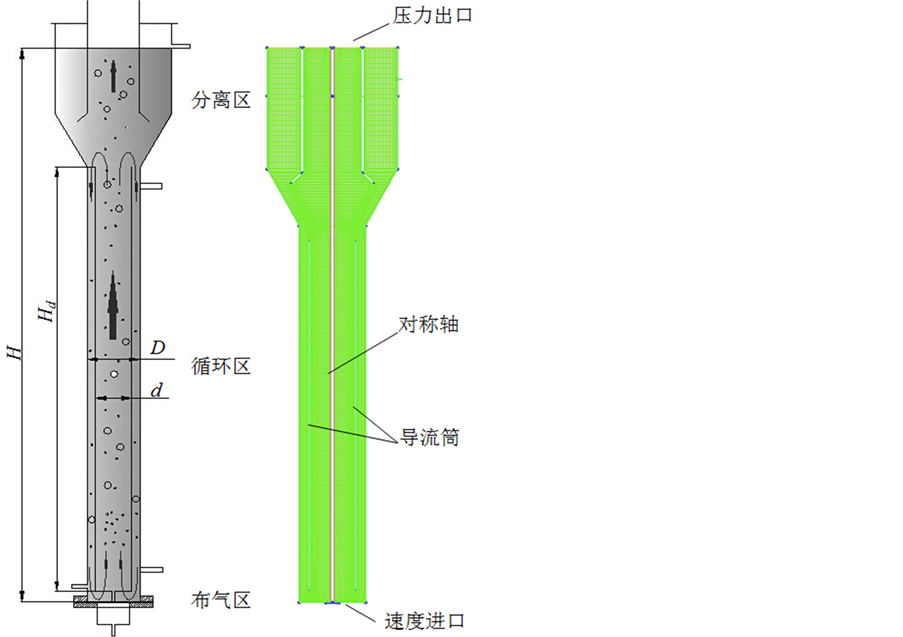
Figure 1. Structure diagram of internal loop three-phase fluidized bed and figure of meshing
图1. 内循环三相流化床结构示意图与网格划分图
根据反应器的轴对称结构特征,对计算流场进行合理简化,采用二维轴对称模型。利用前处理软件ICEM对反应器进行网格划分,结果如图1所示。经网格无关性验证,网格基本尺寸为1.5 mm,边界层尺寸为0.2 mm。网格数为37,819个。
2.2. 计算模型的确定
2.2.1. 计算模型及其假设条件
由于反应器流场包含气-液-固三相,所以采用Euler三相流模型对三相内循环流化床反应器中流场进行数值模拟。对计算模型进行如下假设:
1) 水为连续相,空气和载体颗粒为分散相,流动视为不可压缩的等温流动。
2) 气相和颗粒视为具有均匀直径的球体,其直径分别为3 mm和0.75 mm,通过粘度力考虑颗粒间的作用力。
3) 气-液-固三相,系统与外界之间没有质量交换。
2.2.2. 湍流模型的确定
由于三相流化床内循环的结构特征,在内部流场中会发生流线的弯曲,以及固相颗粒和气相的共同影响,而产生漩涡。故湍流模型采用Realizable k-ε模型[8] 。其控制方程如下:
 (1)
(1)
 (2)
(2)
2.2.3. 基本控制方程
质量守恒方程[8]
 (3)
(3)
动量守恒方程[8]
 (4)
(4)
2.2.4. 相间动量系数模型的选择
在气-液相间和液-固相间都是由牛顿粘性力相互作用。所以气-液相间动量系数采用symmetric模型,液-固相间动量系数采用Gidaspow模型;
气-固相在欧拉三相流模型中均作为分散相处理,由于在气泡附近的固体颗粒有随气泡运动的趋势,因此,气-固相间作用力可以采用类似连续相和分散相间作用力的处理方式 [9] ,故本研究中气-固相间动量系数采用Schiller and Naumann模型。
2.3. 边界条件和初始条件
反应器计算边界条件采用速度进口,分别对进气量为100~700 L/h (即进气速率Ug = 0.33~2.30 m/s)7个工况进行模拟;出口边界条件设置为压力出口边界;壁面边界条件选用默认非滑移边界条件;根据反应器进口边界条件初始化计算。
2.4. 求解参数设置
利用Fluent求解器进行数值求解。采用SIMPLE求解压力耦合方程组的半隐式方法;动量、湍动能以及湍流耗散率的离散方法采用一阶迎风差分格式,默认松弛因子。设置计算时间步长设为10−5 s,计算过程中根据收敛情况逐步增大时间步长到5 × 10−4 s,计算10万步以上。反应器运行时间20 s以上。在轴向高度H = 400 mm处设置监视截面,观察平均液速和平均气速的变化。
3. 结果与讨论
图2所示为进气速率为100 L/h (0.33 m/s)工况下,反应器H = 400 mm处的平均液速和平均气速的变化规律。由图可得,反应器运行8 s后,监视截面的平均液速和平均气速不再随计算时间而变化,说明反应器运行达到稳态。以下讨论结果取8 s后进气速率为400 L/h (1.31 m/s)的反应器运行状态进行分析讨论。
3.1. 气含率分布情况
图3所示为反应器升、降流区气含率轴径向分布情况。由图中可以看出:1) 气含率在径向分布不均匀,呈中心高,边壁低的特点,且气含率径向分布峰值偏离轴心。这主要是由于反应器的曝气孔主要集中在导流筒底部中心区域,气体进入反应器底部时受射流和降流区液相回流引起的缩口的共同作用,使气泡向中心区域聚集;气泡在导流筒上升过程中出现气泡摆动现象,从而导致峰值偏离轴心。2) 随轴向高度的升高,气含率的径向分布呈逐渐均匀的趋势,气含率峰值逐渐向边壁靠近。当轴向高度较小时,由于气体刚进入反应器,喷射动能较强,其射流宽度较窄,所以中心区域的气含率峰值较高;而随着轴向高度的增加,气体动能下降,气体射流的宽度增加,中心区域的气含率峰值下降,且峰值所对应的径
向位置更偏于内筒壁,气含率的径向分布逐步变得平缓;当轴向高度大于0.4 m后,气含率的径向分布基本保持不变。
3.2. 固含率分布情况
反应器中固含率的轴径向分布如图4所示。由图可知:固含率径向分布峰值位于边壁附近,而中心区固含率径向分布相对均匀,且不同轴向高度的径向分布形式接近。此时内循环流化床升流区表现出来典型的环核结构特点[10] 。在升流区的中心核心区域,由于固体载体在导流筒底部的加速非常快,所以在中部的气液固三相流很快达到了充分发展的状态,固含率在中心区域分布较为均匀;而在壁面附近的固含率相对较高,则是由于边壁效应所致[11] ,部分载体颗粒碰撞壁面产生径向运动的分量,但这部分载体能量不足以使它穿过轴向运动流体域到达反应器中心,从而在边壁附近颗粒团聚现象[12] ,因而在壁面附近的固含率相对较高。反应器降流区同样也是呈环核分布的特点。
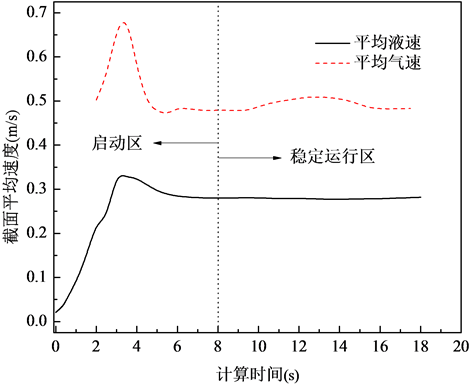
Figure 2. Average velocity of fluidized bed section with time
图2. 流化床截面平均速度随时间的变化
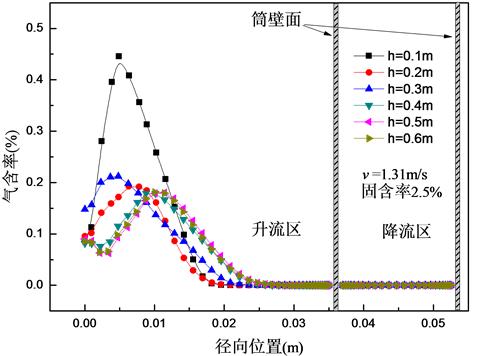
Figure 3. The radial distribution of gas holdup on different heights
图3. 不同高度位置处气含率的径向分布
3.3. 液速的分布情况
图5表示升降流区液相速度的轴径向分布规律。由图可得:1) 反应器升、降流区液相速度分布基本呈中心对称形式,对称轴中心液速最大,向壁面方向逐渐减小降为0;2) 在轴向上,升流区液相速度随轴向高度的增加,径向分布更加均匀,当轴向高度大于0.5 m升流区液速充分发展,液速分布基本保持稳定;降流区液速径向分布则不随轴向高度的增加而变化。究其原因,反应器轴向高度较低时气含率径向分布集中于导流筒中心区域,气液相间作用力较强,液体速度较大,随着轴向高度的增大,气相向导流筒边壁分散,使得液相流速径向分布更加均匀。降流区气含率极低,即在此区域没有气泡或只有少量气泡进入,气液相间作用小,所以降流区液速径向分布不随轴向高度的变化而改变。
4. 结论
利用CFD数值模拟软件,采用Euler三相流模型对内循环三相流化床进行数值模拟,计算结果能够
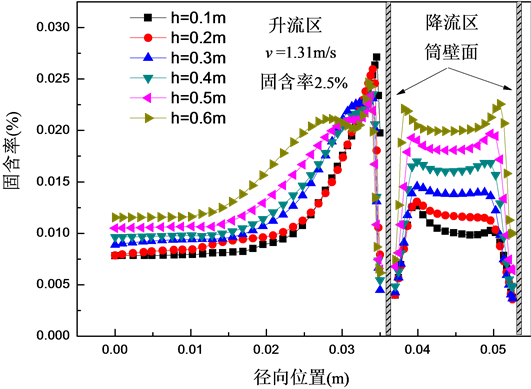
Figure 4. The radial distribution of solid holdup on different heights
图4. 不同高度位置处固含率的径向分布
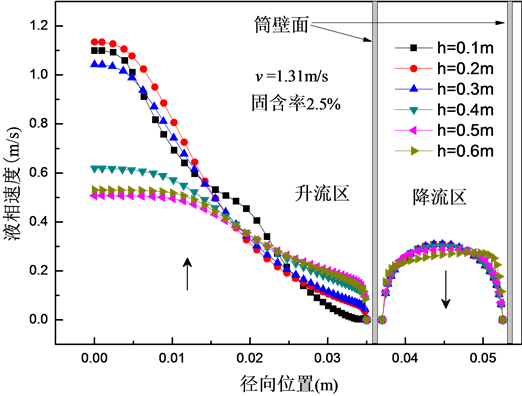
Figure 5. The radial distribution of liquid velocity on different heights
图5. 不同高度位置处液相速度的径向分布
较好的表征反应器中各相的局部流体力学行为。得到如下结论:
1) 内循环三相生物流化床反应器在循环段的气含率径向分布呈中心高边壁底的特点,且峰值出现在偏离轴线位置的地方。气含率随轴向位置的升高分布更加均匀,当轴向高度大于0.4 m后,气含率的径向分布基本保持不变。
2) 反应器升流区和降流区的固含率径向分布峰值位于边壁附近,而中心区固含率径向分布相对均匀;不同轴向高度的径向分布形式相似,且随高度增加而变大。
3) 反应器升流区液相速度径向分布不均匀,呈中心高而边壁低的抛物线规律,且随轴向高度的增大不均匀性减弱,当轴向高度增加到0.5 m时,液速径向分布基本保持不变;降流区液速径向分布呈明显的管流特征,且不随轴向高度的改变而变化。