1. 引言
传统的自动化立体仓库每存放或者取出一个托盘时，都需要堆垛机进入货架内部进行作业。每进行一次存货或者取货任务，堆垛机进行一次这样的任务，而且一般一次只能够取一个托盘，或者取两个位置相近的货物。这样，自动化立体仓库的工作并不能够节约时间。
以动力贯通式货架和提升穿梭车为核心的高密度敏捷配送系统能够实现托盘的敏捷出库和敏捷入库。在本仓储系统中，托盘能够实现连续地存放，这样极大地提高了仓储系统空间利用率，同时能够极大地提高出库效率。系统中存放多种大批量的货物，不同货物具有多种不同的属性。具体的某种货物具有具体的某种属性，而对于这些货物，应该哪一种货物存放在哪一个货道中，才能够提高本仓储系统的出入库效率，减少物流的总成本，同时保持货架的稳定性，这就涉及到货位分配的问题。
如果货位的分配是散乱随机的，就达不到敏捷配送的目的。为了方便货物能在现有的条件下更快的出入库，需要把相应的货物存入合适的货位，这就涉及到货位优化。数量大的货物放在高层货架，每次存取货都执行高层货架的存取货动作，也是十分费时的。因此，进行合理的货位优化是非常有意义的。
进行货位优化时，要同时考虑货物的出入库频率、货物的重量和数量等多个因素，因此，这是一个多目标组合的优化问题。设计合适的货位分配方式Atmaca和Ozturk [1] 建立了一个仓储货位分配的数学模型并使用模拟退火算法进行了求解。Mansuri [2] 提出了一种AS/RS系统货位分配的循环时间评估模型。Malmborg和Al-Tassan [3] 提出仓储管理方面的一个数学模型，评估库存管理系统的吞吐能力、库存服务水平和快速响应能力。Berg和Zijm [4] 提出了一个随机的仓储管理模型。Lee等人 [5] 设计了一种自动存储系统的货架结构。Tunç等人 [6] 通过优化拣货策略来改善仓储系统的拣货作业时间。Moccia等人 [7] 提出了一个处理时间段的动态分配模型。Azzi等人 [8] 提出了一个计算旅行时间的新方法。Petersen和Aase [9] 测试了拣选、仓储和路径优化三个过程对决策的影响。Potrc [10] 提出了一种AS/RS系统中评估时间的旅行时间模型。石梦竹 [11] 根据动力贯通式货架的自动化立体仓库的特点，建立了货位分配和入库调度的数学模型，分别采用遗传算法和蚁群算法进行了求解。
所有的研究在一组特定的假设下讨论货位分配模型：考虑到的AS/RS设计参数的变化范围广，这一论文建立了系统整体的分析。
2. 问题概述
以动力贯通式货架和提升穿梭车为核心的高密度敏捷配送系统能够实现托盘的敏捷出库和敏捷入库。动力贯通式货架是一种连续的贯通式货架，同时基于货架滚轮和自行轨道车的结构设计，它能够实现在内部提供动力，这样，货物在货架的内部就能够实现连续地前移。在本仓储系统中，前方的托盘出库后，后面的托盘能够自动地运行至货架的出库端位置，同时后面的托盘能够自动地运行至前方托盘位置，有效地避免了传统货架货位空缺的现象。
本系统中，位于一层的货架位置能够实现托盘的连续出库和连续入库。对于高层的货架，只能够进行单一托盘的存取货操作，同时执行高层货架的存取货任务时还需要提升穿梭车执行提升动作。因此相比第一层的货架，高层货架的存取货效率要低得多。重量大的货物都存放在了高层，重量小的货物存在了第一层，会使得货架整体的重心位置偏高，使货架的稳定性得不到保证。
进行货位优化时，要同时考虑货物的出入库频率、货物的重量和数量等多个因素，因此，这是一个多目标组合的优化问题。
3. 多目标优化问题
不解决含有多个目标和多约束的优化问题称为多目标优化问题。在工程实际应用中，工程优化的问题大多数是多目标优化问题，有时需要使多个目标在给定的区域内都达到最优，而目标之间却是相互冲突。如本文中的货位优化问题，希望货物的出入库频率最高的位于最下层，数量大的位于最下层，重量大的位于最下层，有时重量小的反而出入库频率高。这种多目标优化问题一般的数学模型可以描述为
(1-1)
式中，
表示向量的极小化，即目标函数中各个子目标函数都尽可能达到最小化。
设是多目标优化模型的约束集，是多目标优化时向量目标函数，且有。若
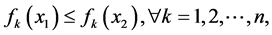
且
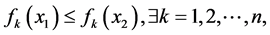
则称解x1比解x2优越。
设是多目标优化模型的约束集，是多目标优化时向量目标函数，且有且x1比X中所有其它的解都优越，则称是多目标优化模型的最优解。由此可知，解使得所有(
)都达到最优，但实际中一般不存在这样的解。
设是多目标优化模型的约束集，是多目标优化时向量目标函数，且有且不存在比更优越的解x，那么称解是多目标优化模型的Pareto最优解。由此可知多目标优化模型的Pareto最优解是问题的一个可以接受的“非劣解”。且在一般的实际问题中，往往存在多个Pareto最优解。
对于求解多目标优化问题的Pareto最优解，目前已经由了多种基于遗传算法的求解方法，权重系数变换法是一种在实际应用中经常用的方法。对一个多目标优化问题，给每个子函数(
)赋予权重，其中是相应在多目标优化问题中的重要程度，那么各个子目标函数的线性加权和表示为
(1-2)
如果将此函数作为多目标优化问题中的评价函数，则多目标优化的问题就可转化为单目标优化的问题了，可以利用单目标优化的遗传算法来解决多目标优化问题。
4. 货位分配模型的建立
论高密度敏捷配送系统中动力贯通式货架的货位分配需要考虑不同种类货物的出入库频率、货物的数量和重量、货架的稳定性，同时考虑库区的分配策略，这是一个多目标组合优化问。
动力贯通式货架的平面布局如图1所示，货架是多层的立体货架，每一层货架具有多个货道，货道是连续贯通的，针对一个固定的货道只存放一种类型的货品。有两台提升穿梭车分列在货架的两端分别进行出库和入库的作业，出入库的站台分别在货架两端提升穿梭车的外侧。
由于动力贯通式货架的每一个货道只存放同一种货物，并且当货品进入端口位置后，系统能够实现让货品自动运行至出口端。因此在进行货位分配时，可以将一个货道作为一个量表示，不需要考虑货品在货道中的位置，只需要考虑货物存放于货架的第几层第几列。
以某太阳能产品配送中心作为工程背景，研究某光伏产品零件的特征，建立相应的货位分配优化模型。根据其产品特点，可以忽略产品相关性对货位分配模型的影响；同时由于采用标准托盘，同时货架的设计能够满足所有产品的尺寸要求，也可以忽略产品尺寸对模型的影响；同时，各个零件的腐蚀性、保存期限和易碎程度也相差不大，也可忽略这些属性对模型的影响。而对建立高密度敏捷配送系统货位优化模型影响最大的因素是托盘货物的重量、数量和出入库频率。
假设动力贯通式货架具有p列q层，从下至上是第1层至第p层，从左至右是第1列至第p列。第1层能够实现敏捷配送，越往上，出库效率越低；而第1列是最方便出库的位置，位置越靠由，出库的效率越低。第x列y层的货道为
(见图2)。各货道的高度、宽度和长度相同，忽略提升穿梭车启动和制动的时间。由于托盘使用标准托盘，尺寸相同，则每个货道能够存放托盘的最大数量相同，为。货道的高度为H，其中货道的高度包括了货物承载层高度和轨道车运行层的高度，宽度为W，长度为L。
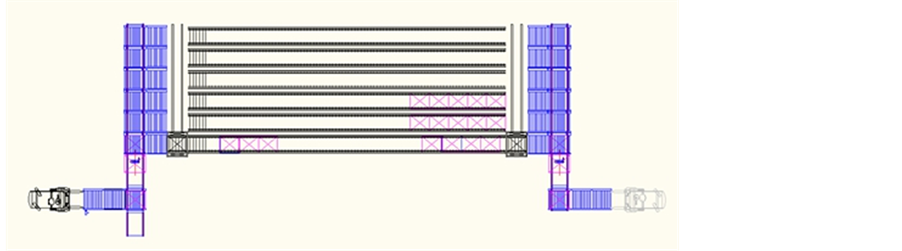
Figure 1. The plan of power drive-through rack
图1. 动力贯通式货架平面图
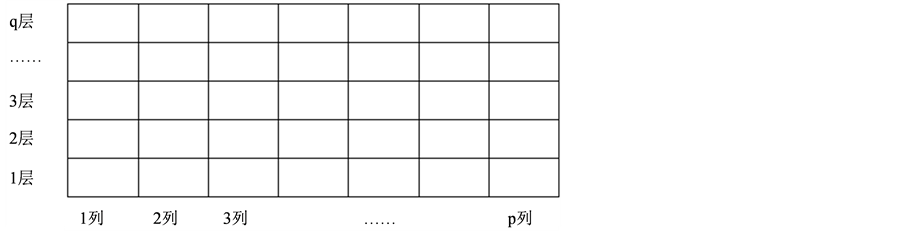
Figure 2. The diagram of power drive-through rack
图2. 动力贯通式货架货位示意图
1) 考虑货架的稳定性，使其上轻下重，受力均匀，目标函数为：
(1-3)
式中——处于货道
上单一货物的重量；——货道
中货物的数量。
考虑到货架的稳定性，使其重心降低，货架整体的高度一般小于其整体的宽度。故有
(1-4)
2) 假设进行单个货物的入库作业，且每完成一个工作任务，系统都回到初始状态。如果进行单个货物出入库操作的效率最高，那么在进行连续出入库操作时，本货道作业同样能够效率最高。考虑货物出入库频率大的货物优先入库，使货架上货物出入库效率与提升穿梭车运行时间的乘积之和即货物总的出入库时间最小，建立数学模型
(1-5)
其中：
(1-6)
式中——处于动力贯通式货架中
货道上货物的出入库频率；——货道
上的货物入库所用时间；——提升穿梭车水平方向平均运行速度；——提升穿梭车竖直方向平均运行速度。
综上所述，高密度敏捷配送系统的货位分配优化模型为：
(1-7)
约束条件为：
且
是整数。
5. 货位分配方式改进
为使高密度敏捷配送系统在进行出库作业时达到更高的效率，并且方便出库，同时缩短客户的等待时间，可在原有分配方式的基础上改进。前面的数学模型，综合考虑了货架的稳定性和货物的出入库频率，能够达到较优的货位分配方式。
在实际的工作中往往会出现这种情况，客户需要货品时，会提前几天或一天进行货物的预定，到那一天时再进行货物的配送，而这一批货物中却会有多种不同类型的货品。在这种情况下，如果等到货物配送时再进行货物的出库，则需要提升穿梭车在动力贯通式货架的不同货道间往复运行，而自行轨道车也在货架的货道内部不断地往复运行，尤其有时种类很多，但是每种只取1个托盘时，提升穿梭车和自行轨道车更需要不停地运行，这在一定程度上浪费了很多时间。而有些时候货物出库是很集中的，这在一定程度上增加了等待时间。而有些时候货物的出库任务是很少的，系统处于闲置状态。这样使得整个的工作时间并不协调。
为了协调系统的出库工作，节省系统总的出库时间，提高出库的效率，进一步减少客户的等待时间，在货位原有的分配基础上做了如下改进。在动力贯通式货架的第1层货架中选取1个或者2个货道作为备货货道。其它的货道进行正常的货位分配。如图3所示，这是一个3层6列的动力贯通式货架，货道内的数字是对货道的编码，从第3号货道到第18号货道按照上面的数学模型进行货位分配，而备1和备2作为备货货道。
在前一天下午的空闲时间，可以根据第二天订单的先后出货顺序，将第二天将要出库的不同种类的货物提前存放在备货货道中，并且按订单的顺序进行排放。
出库时，按照订单的顺序，先将备1货道中的货物按前后的顺序进行出库，备1货道中的货物出库完成后，再将备2货道中的货物出库。按先后顺序将提前准备的订单货物全部完成出库后，继续进行出库任务时，即可按照正常的出库流程进行出库。以表1中的订单信息进行说明。
表1中的订单信息为第二天早上出库的货物信息，在前一天的空闲时间，系统将订单中的货物A、B、C、D、E五种类型的货物按订单的顺序分别从五种货物所对应的货道中取出，存入备货货道中。那么根据订单的信息所确定的货物排放顺序就是A-A-B-C-C-B-B-C-C-D-D-D-A-B-C-D-D-E。
由于系统能够实现货物的自动前移，那么第一批货物A-A-B-C-C完成出库后，第二批货物B-B-C-C-D-D-D就自动前移到出库端的前面等待出库，出库时也能够很快完成作业。同时多个托盘还能够实现连续出库，当订单的数量小于自行轨道车所能推动托盘的最大数量时，自行轨道车的一次取货操作就能够将订单中的货物完成出库操作；订单数量大时也只需进行几次操作就可以了。
6. 结论
论文中讨论了高密度敏捷配送系统的货位分配模型并提出了新的分配模型。该模型通过分析动力贯通式货架的货位分配解决了多目标优化问题并确定了货位分配的原则。效率优先原则和先进先出原则是最重要的原则。
论文通过数学模型和货位分配原则得到了以下结果：当货架为3层6列时，将货位1和货位2设为备用货道可以大大减少出库时间并使其他货道正常执行出库任务。
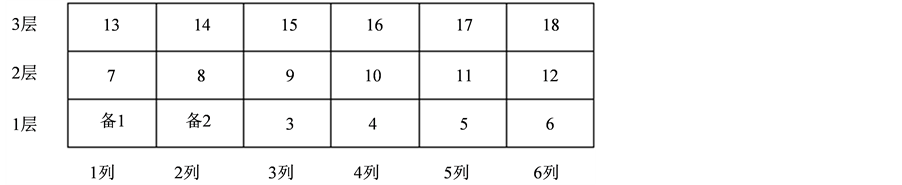
Figure 3. The diagram of location improvement of power drive-through rack
图3. 动力贯通式货架货位分配改进示意图
Table 1. Order information for the next morning
表1. 第二日早晨订单信息
该模型考虑了货位分配。基于类的货位分配原则可以对系统的行程时间有显著的影响(Manzini等人 [12] )。为了这个原因，可以建立一个新的模型来研究高密度敏捷配送系统货位分配的影响。另一个领域的研究，关于动力贯通式货架，并使用蚁群算法来处理货位分配优化的研究。由于蚁群算法强大的功能，这个新的系统是比传统的行程时间更理想。