1. 引言
1957年,Craig首次提出了插值的概念[1] 。在此后的研究中,研究者们发现Craig插值在命题逻辑、命题可满足性(SAT)问题[2] [3] 、无量词一阶逻辑问题[4] 、可满足性模理论(SMT)问题[5] 、软件模型检测[6] 和抽象优化[7] [8] 等领域有广泛的应用,因此,其中所涉及的插值的求法成为研究的热点。当前最常用的求插值的方法为DPLL法[9] ,它因易操作、高效等优点被广泛使用。由DPLL的研究可知,它可与理论T结合,因此插值的研究可扩展到理论中去。
近些年来,由于实际研究的需要,理论插值的研究越来越广泛。研究的理论包括线性不等式理论[10] 、数组理论[11] 、未解释函数理论[12] 等。但这些都局限于对单个理论的研究,当面对两个或两个以上理论时,就无法高效地求出插值了。本文研究的是两种理论结合下的插值,即线性不等式理论(Linear Inequality,简称LI)和未解释函数理论(Uninterpreted Functions,简称UF)结合下的插值,这里将这种结合理论称为LIUF理论。LIUF理论中非协调公式对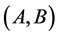 的插值
的插值 满足:(1)
满足:(1)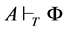 ,(2)
,(2) ,(3)
,(3) 中的符号都是
中的符号都是 公有的。
公有的。
LIUF理论在软件模型检测中有十分重要的应用。同时,当已知LI理论的插值时,可通过结合理论下的插值算法求出UF理论的插值,反之亦然,这大大减少了工作量。然而,现有的工作仅研究了无量词公式在LIUF理论中的插值算法,量词公式的插值算法仍是一个未解决的问题。
LIUF理论量词公式插值求解面临两大问题,即如何消去量词以及如何消去插值中由量词消去引入的新变量。针对所面临的问题,本文提出了LIUF理论量词公式的插值算法,并通过实例详细地说明了如何在LIUF理论中求出量词公式的插值。
2. LIUF理论
在LIUF理论中,项是单个变量或 ,这里
,这里 是项,
是项, 是
是 元函数符号。形如
元函数符号。形如 的线性组合称为算术项,其中
的线性组合称为算术项,其中 是项,
是项, 为整数常量,且
为整数常量,且 ,
, 。原子谓词指单个命题变量或不等式
。原子谓词指单个命题变量或不等式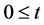 (这里
(这里 是算术项)或等式
是算术项)或等式 (这里
(这里 是项)。原子谓词本身或原子谓词的否定构成文字,文字的析取构成子句,子句通常用“
是项)。原子谓词本身或原子谓词的否定构成文字,文字的析取构成子句,子句通常用“ ”表示,将包含文字集
”表示,将包含文字集 的子句记作
的子句记作 ,空子句记作
,空子句记作 。
。
序列是有限公式集的序列对,记为 ,其中
,其中 为公式集(本文中为文字集或子句集),
为公式集(本文中为文字集或子句集), 为公式的合取,
为公式的合取,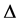 为公式的析取。现设本文所讨论的插值均有如下形式:
为公式的析取。现设本文所讨论的插值均有如下形式: ,其中
,其中 为公式对,括号中的
为公式对,括号中的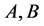 也可表示为
也可表示为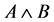 ;
; 代表与
代表与 有关的插值,当
有关的插值,当 为空子句时,
为空子句时, 就是
就是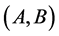 的插值,这里的插值以及下文所提到的插值均为Craig插值。通常,
的插值,这里的插值以及下文所提到的插值均为Craig插值。通常, 满足:
满足: ,
,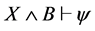 。需要说明,文中所有的小写字母都代表公式,大写字母都代表公式集。
。需要说明,文中所有的小写字母都代表公式,大写字母都代表公式集。
现给出证明规则,使用这些规则可得到 的证明过程。
的证明过程。
HYP  COMB
COMB 
RES 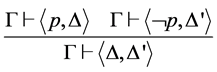 TRANS
TRANS 
CONG  (*) EQNEQ
(*) EQNEQ 
LEQEQ  EQLEQ
EQLEQ 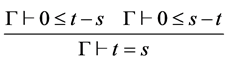
本文中(*)表示出现在“ ”右侧的符号也出现在其左侧。
”右侧的符号也出现在其左侧。
例 设 ,
, ,试写出
,试写出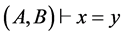 的证明过程。
的证明过程。
1  (HYP) 2
(HYP) 2  (HYP)
(HYP)
3  (HYP) 4
(HYP) 4  (HYP)
(HYP)
5  (COMB1, 3) 6
(COMB1, 3) 6  (COMB2, 4)
(COMB2, 4)
7  (EQLEQ5, 6)
(EQLEQ5, 6)
3. LIUF无量词理论公式的插值
上节介绍了 的证明过程,而插值正是从这个证明过程中推出的,那么如何从中提取出插值呢?这正是本节所要讨论的内容:介绍LIUF理论中三个无量词公式理论插值的定义,引入插值规则,讨论插值的求法。
的证明过程,而插值正是从这个证明过程中推出的,那么如何从中提取出插值呢?这正是本节所要讨论的内容:介绍LIUF理论中三个无量词公式理论插值的定义,引入插值规则,讨论插值的求法。
定义1(不等式插值)将形如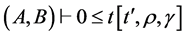 序列的称为不等式插值,其中
序列的称为不等式插值,其中 为文字集,
为文字集, 为项,
为项, 为公式。它是有效的,满足:
为公式。它是有效的,满足:
(1) ;
;
(2) 且
且 ;
;
(3) ,
, ,
, 。
。
这里,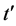 为插值。符号“
为插值。符号“ ”在
”在 中表示
中表示 中所有的变量和未解释函数符号都出现在
中所有的变量和未解释函数符号都出现在 中;在
中;在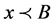 中表示
中表示 中所有的变量和未解释函数符号都出现在
中所有的变量和未解释函数符号都出现在 中,此时称
中,此时称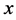 是全局项;否则,称
是全局项;否则,称 是局部项。在不等式理论中,
是局部项。在不等式理论中,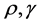 总为
总为 。
。 表示
表示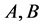 中不等式的线性组合,
中不等式的线性组合, 表示对
表示对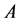 中不等式相加后得到的结果。
中不等式相加后得到的结果。
定义2(子句插值)将形如 的序列称为子句插值,这里
的序列称为子句插值,这里 是子句集,
是子句集, 是文字集,
是文字集, 是公式。它是有效的,满足:
是公式。它是有效的,满足:
(1) ;
;
(2)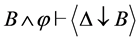 ;
;
(3) 。
。
这里, 表示
表示 中文字的原子谓词出现在
中文字的原子谓词出现在 中,
中,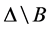 表示
表示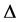 中文字的原子谓词不出现在
中文字的原子谓词不出现在 中。在子句插值中,
中。在子句插值中,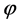 就是插值。
就是插值。
定义3(等式插值)将形如 的序列称为等式插值,其中
的序列称为等式插值,其中 是文字集,
是文字集,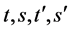 为项,
为项, 为公式。它是有效的,满足:
为公式。它是有效的,满足:
(1) ;
;
(2) 
①  ;
;
②  ;
;
(3) ,
, ,如果
,如果 ,那么
,那么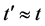 ,否则
,否则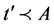 ,
, 同理。
同理。
这里,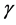 为插值。为了得到
为插值。为了得到 ,首先建立
,首先建立 的等式链
的等式链 ,等式链中的等式来自于
,等式链中的等式来自于 或
或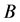 ,设
,设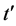 代表等式中最左侧的全局项,
代表等式中最左侧的全局项,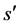 代表等式中最右侧的全局项。当等式中有全局项时,由
代表等式中最右侧的全局项。当等式中有全局项时,由 可推出
可推出 ,
, ;当等式中无全局项时,有
;当等式中无全局项时,有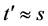 ,
, 。在TRANS规则中,
。在TRANS规则中,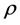 总为
总为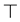 。
。
下面介绍几种插值规则,运用这些规则,就可以得到插值。
首先介绍前提(HYP)规则:
HYP-A 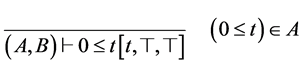 HYP-B
HYP-B 
HYPC-A  HYPC-B
HYPC-B 
HYPEQ-A 
其中
 ,
,
HYPEQ-B 
HYP规则应用在插值算法的最开始,主要作用是将 中的公式写成
中的公式写成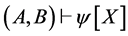 的形式,方便下面的运算。
的形式,方便下面的运算。
下面介绍其余插值规则,这些规则的使用并无固定顺序,可根据实际需要选择恰当的规则计算插值。
COMB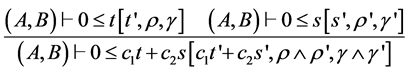 ,
,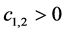
RES-A ,
, 不出现在
不出现在 中
中
RES-B ,
, 出现在
出现在 中
中
TRANS1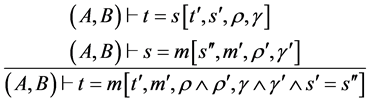 ,
, 且
且
TRANS2 ,
, 或
或
其中 ,
,
CONG1 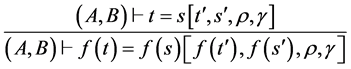 (*),
(*),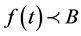 或
或
CONG2  (*),
(*),
LEQEQ1 ,
, 或
或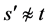
LEQEQ2 ,
,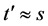 ,
,
EQLEQ-BB 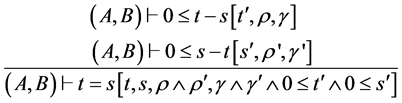 (*),
(*), ,
,
EQLEQ-AB 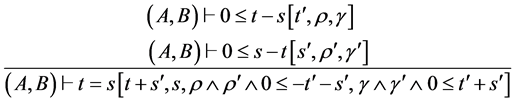 (*),
(*), ,
,
EQLEQ-AA  (*),
(*), ,
,
4. LIUF理论量词公式的插值算法
4.1. 面临的挑战
通过上一节的介绍可以很容易证明出LIUF理论无量词公式插值系统的完备性和可靠性。但在某些情况下,无量词公式插值通常是不存在的。例如: ,
, ,
, 的插值为“存在
的插值为“存在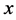 ”,这是量词的表达方法。因此,对于单纯的整数域上的LIUF理论无量词公式,并不能得到完备的系统,这就需要研究带有量词公式的LIUF理论插值系统。
”,这是量词的表达方法。因此,对于单纯的整数域上的LIUF理论无量词公式,并不能得到完备的系统,这就需要研究带有量词公式的LIUF理论插值系统。
LIUF理论量词公式的插值求解过程中,如何消去量词成为首个要面临的问题。量词包括存在量词和全称量词。存在量词可用斯科拉姆化法[13] 消去,这是很容易做到的;但消去全称量词就有些复杂了,全称量词的消去过程会引入新的变量,那么新变量的选择就变得至关重要,如果选择不当,就会增加不必要的计算量,而且当公式中同时含有存在量词和全称量词时,必须考虑先消去哪种量词,这关系到整个插值过程的工作量。
当消去量词后,原公式变为无量词公式,然后求出无量词公式的插值。应注意:消去量词后得到的公式可用无量词公式插值算法计算。但此时求出的插值并不是所要求的量词公式的插值,因为其中含有由量词消去所引入的新变量,这时需要考虑如何消去新变量,且保证不会影响插值的整体形式。
针对上述问题,要求出LIUF理论量词公式的插值,需要满足:
1) 确定消去存在量词和全称量词的顺序和方法;
2) 找到无量词公式插值中引入的新变量的消去方法。
4.2. LIUF理论量词公式插值算法
对于上述问题,我们给出LIUF理论量词公式插值算法。该算法可以解决上节所提出的两个问题,并能成功求出其插值。对于量词公式对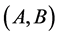 ,若仅出现一种量词,就用相应的方法消去量词,若两种量词同时出现,则先消去存在量词,然后再消去全称量词,并将公式变为无量词的情况
,若仅出现一种量词,就用相应的方法消去量词,若两种量词同时出现,则先消去存在量词,然后再消去全称量词,并将公式变为无量词的情况 ,然后通过已有的插值算法先求出
,然后通过已有的插值算法先求出 的插值
的插值 ,再由文献[1] ,将
,再由文献[1] ,将 中由量词消去引入的新变量用存在或全称量词替换,就得到了
中由量词消去引入的新变量用存在或全称量词替换,就得到了 的插值。算法的具体过程如算法1所示。
的插值。算法的具体过程如算法1所示。
算法1. LIUF理论量词公式的插值算法
4.3. 算法实例
使用LIUF理论量词公式插值算法可以求出量词公式的插值。下面以具体例子进行说明。
例 设 ,
,  ,求
,求 的插值
的插值 。
。
1) 用斯科拉姆化法消去存在量词,并把公式变为全称前束范式。
 ;
;

2) 消去全称量词,将 中的项
中的项 实例化,分别引入新变量
实例化,分别引入新变量 和等式
和等式 ,将量词公式对
,将量词公式对 化为无量词公式对
化为无量词公式对 。
。
 ;
;
 ;
;
3) 由LIUF理论无量词公式的插值算法求出 的插值
的插值 。
。
具体步骤如下:
(1)  (HYP-A)
(HYP-A)
(2) 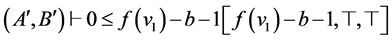 (HYP-A)
(HYP-A)
(3)  (HYP-A)
(HYP-A)
(4) 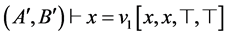 (HYPEQ-A)
(HYPEQ-A)
(5)  (HYP-B)
(HYP-B)
(6)  (HYP-B)
(HYP-B)
(7)  (HYP-B)
(HYP-B)
(8)  (HYPEQ-B)
(HYPEQ-B)
(9) 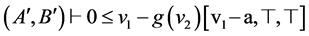 (COMB1, 5)
(COMB1, 5)
(10)  (COMB2, 6)
(COMB2, 6)
(11)  (LEQEQ2 4)
(LEQEQ2 4)
(12)  (LEQEQ1 8)
(LEQEQ1 8)
(13)  (COMB9, 11)
(COMB9, 11)
(14) 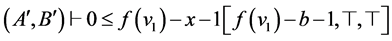 (COMB10, 12)
(COMB10, 12)
(15)  (COMB13, 14)
(COMB13, 14)
(16)  (COMB3, 7)
(COMB3, 7)
(17) 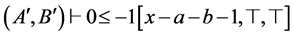 (COMB15, 16)
(COMB15, 16)
所以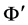 为
为 。
。
4) 因为 中不含有新变量,所以不需要将变量替换为量词。
中不含有新变量,所以不需要将变量替换为量词。
所以, 的插值
的插值 为
为 。
。
有了上述算法,无量词公式的插值规则都可以应用在带有量词公式上,这就使插值有了更广泛的应用。
5. 结语
本文在无量词理论插值算法的基础上,介绍了LIUF理论量词公式的插值算法,解决了之前无法求解量词公式插值的问题,从而使插值有了更为广泛的应用。但这种方法只能应用在已知的无量词插值算法的基础上,并不能独立使用,进一步的工作是要改进出适用范围更广的插值算法,这将使插值计算更加智能化和高效化。