1. 引言
Al-Mg系具有中等强度，加工性能和焊接性能好，耐腐蚀性能良好，广泛应用于交通运输、建筑装饰、瓶罐制造等领域[1] -[3] 。金属塑性变形过程中的流变应力值决定了加工时设备所需施加的载荷值及能耗，金属高温变形行为受合金化学成分、变形温度、变形程度和应变速率的影响，是变形体内部显微组织演变的综合反映 [4] - [6] 。近年来物理模拟和数值模拟技术在金属热加工领域获得了越来越广泛的应用，为了提高金属热加工数值模拟精度，合理制定材料热加工工艺，必须了解合金高温变形时的流变行为及精确的流变应力值 [7] - [10] 。为此，本文作者以热粗轧态Al-4.5Mg-0.6Mn铝合金为研究对象，采用高温圆柱体等温压缩法研究其流变行为，建立该合金的高温流变应力本构方程，为Al-Mg系合金热加工工艺的制定提供参考。
2. 实验材料与方法
实验用材料为已完全再结晶的Al-4.5Mg-0.6Mn合金热粗轧板材，板材经机加工成Φ10 × 15 mm的圆柱体试样。在Gleeble-3800热模拟机上进行等温压缩实验，压缩温度分别为300℃、400℃、500℃，应变速率分别为0.01、0.1、1、10 s−1，变形量为50%，压缩时试样两端添加石墨片并均匀涂上润滑剂(75%石墨 + 20%机油 + 5%硝酸三甲苯脂)以减小摩擦的影响。加热温度为5℃/s，保温2 min，变形后立即水淬，以保留其高温变形组织。
3. 实验结果与分析
3.1. 流变应力曲线特征
Al-4.5Mg-0.6Mn铝合金在不同变形条件下的流变应力曲线如图1所示。从图1可以看出，峰值流变应力随着应变速率的增加而增大，随着变形温度的升高而降低。在一定变形条件下，Al-4.5Mg-0.6Mn铝合金热压缩真应力随着应变的增加而迅速增大，当应变量超过一定数值时，流变应力随应变的增大变化非常小，应力值趋于稳定，甚至在一些变形条件下，随着应变量继续增大流变应力出现降低现象。总体上来说，图1所示的真应力–应变曲线可以划分为加工硬化阶段、过渡阶段和稳态阶段3个部分。在开始变形阶段，位错不断增殖，并且相互之间交错，随着位错密度的增加，回复的驱动力增大，使得动态
(a) (b)
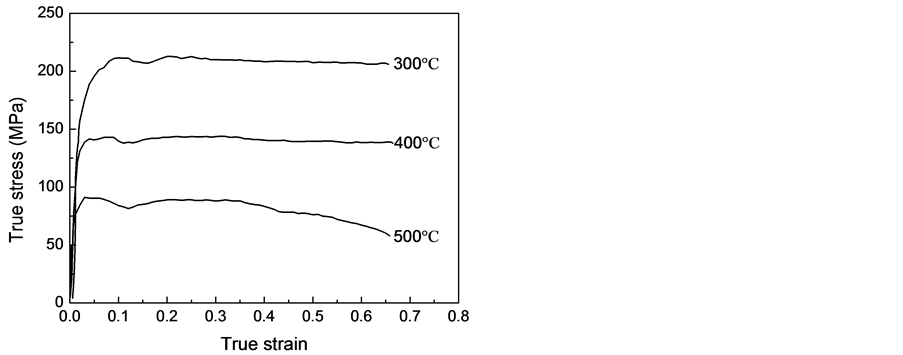
(c) (d)
Figure 1. True stress-true curves of Al-4.5Mg-0.6Mn aluminum alloy under different deformation conditions: (a) έ = 0.01 s−1; (b) έ = 0.1 s−1; (c) έ = 1 s−1; (d) έ = 10 s−1
图1. Al-4.5Mg-0.6Mn铝合金不同变形条件下的真应力–真应变曲线：(a) έ = 0.01 s−1；(b) έ = 0.1 s−1；(c) έ = 1 s−1；(d) έ = 10 s−1
回复的速率也相应增大。当应变量增加到某一个值时，加工硬化和回复软化达到动态平衡，此后的位错密度将保持稳定，这时流变应力也保持不变。值得注意的是，当变形条件为500℃，变形速率为10 s−1时，应力达到峰值后出现明显下降现象，这是发生了动态再结晶的表现。由图1还可知，在同一应变速率下，随变形温度的增大，真应力水平明显下降；在同一变形温度下，随应变速率增加，真应力水平升高，说明Al-4.5Mg-0.6Mn铝合金在该试验条件下具有正的应变速率敏感性。
3.2. 本构方程模型
材料高温变形过程中流变应力、变形速率、变形温度间的关系可用如下关系式进行描述 [11] [12] ：
(1)
其中：A为与温度无关的常数；Q为热变形激活能；R为摩尔气体常数；T为变形温度；f(σ)与应力水平有关的函数。
在低水平应力(ασ < 0.8)下，
(2)
在高水平应力(ασ > 1.2)下，
(3)
整个应力范围内：
(4)
式(2)~(4)中，α、β、n均为与温度无关的常数，且α = β/n。
在所有应力状态下，式(1)可表示为：
(5)
应变速率和变形温度关系可用Z参数表示 [9] [10] ：
(6)
当变形温度T或应变速率
不变时，流变应力σ及其对数与应变速率
的对数(lnσ-ln
, σ-ln
, ln[sinh(ασ)]-ln
)，流变应力σ的对数与温度T的倒数(ln[sinh(ασ)]-1/T)，流变应力σ的对数与Z的对数(ln[sinh(ασ)]-lnZ)之间均满足线性关系。图2~5所示为实验合金在不同变形条件下各关系的线性回归图，由各图中直线斜率的平均值可求得本构方程所需常数，计算得到A = 1.1336 × 1013 s−1，α = 0.0102 MPa−1，n = 6.1407，Q = 178.962 KJ/mol。
将求得的A、α、n、Q等参数代入式(5)，可得Al-4.5Mg-0.6Mn铝合金的流变应力本构方程为：
(7)
为了检测上述本构方程的准确性，根据求得的Al-4.5Mg-0.6Mn铝合金峰值流变应力本构方程，将不同变形条件下的材料参数代入式(7)中计算出不同变形条件下的流变应力。
图6所示为实测流变应力曲线和本构方程计算值的对比。可以看出实测曲线与本构方程预测曲线吻合较好。为了更清晰的评价实测值与计算值之间的误差情况，可引入以下误差分析表达式：
(a) (b)
Figure 2. Relationship between strain rate and flow stress for Al-4.5Mg-0.6Mn alloy: (a) lnέ-σ; (b) lnέ-lnσ
图2. Al-4.5Mg-0.6Mn铝合金的应变速率与流变应力的关系：(a) lnέ-σ；(b) lnέ-lnσ
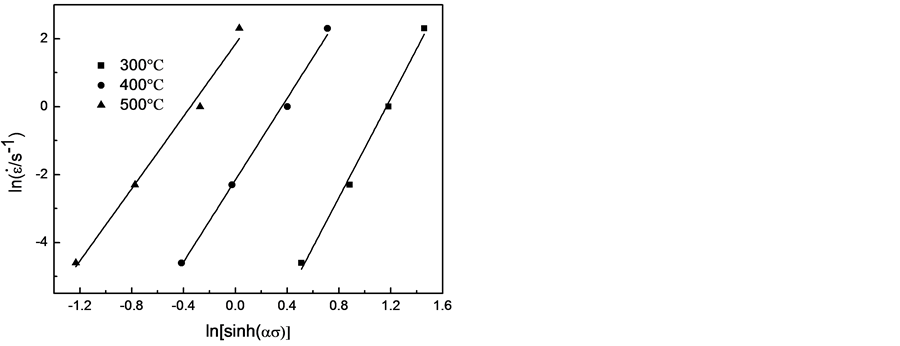
Figure 3. Relationships between flow stress and rate of Al- 4.5Mg-0.6Mn alloy
图3. Al-4.5Mg-0.6Mn铝合金流变应力与应变速率的关系
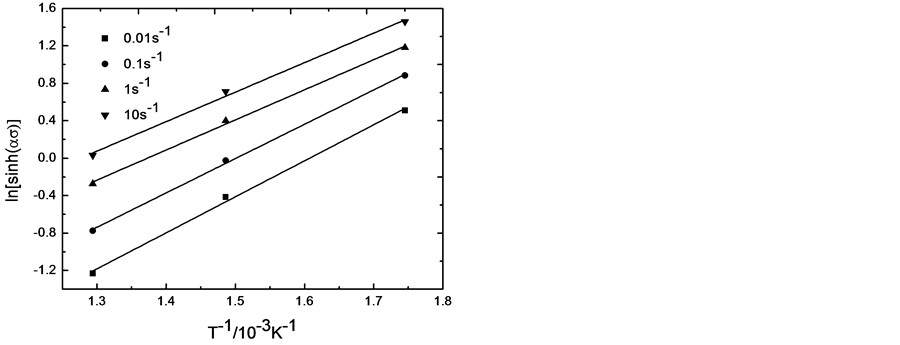
Figure 4. Relationships between flow stress and deformation temperature of Al-4.5Mg-0.6Mn alloy
图4. Al-4.5Mg-0.6Mn铝合金流变应力与变形温度的关系
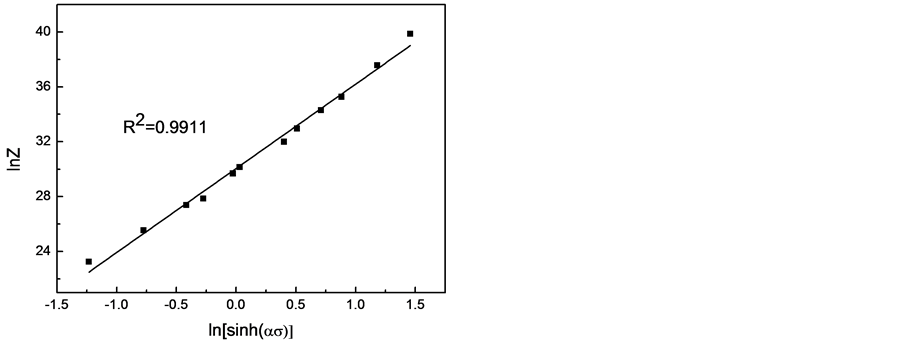
Figure 5. Relationship between flow stress and Zener- Hollomon parameter
图5. Al-4.5Mg-0.6Mn铝合金流变应力与Z参数的关系
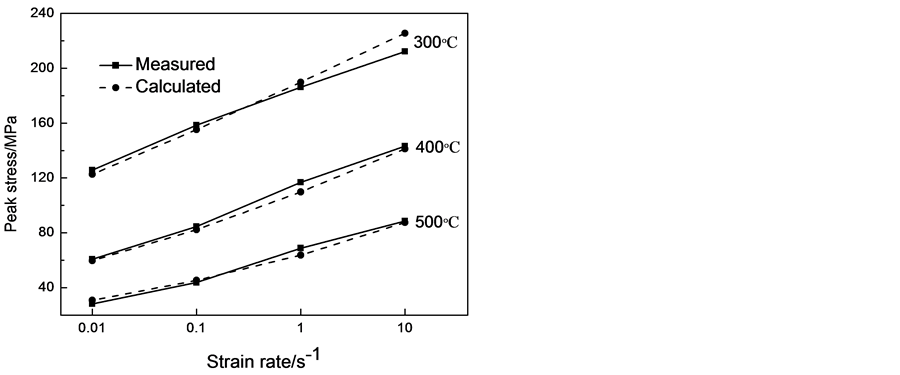
Figure 6. Comparison between measured and calculated value of Al-4.5Mg-0.6Mn aluminum alloy at train rate of 1 s−1
图6. Al-4.5Mg-0.6Mn铝合金在应变速率为1 s−1时实测应力与计算应力值的对比
(8)
(9)
式中：σE为流变应力实测值；σC为本构方程计算值；Rerr为相对误差值；Rave为平均相对误差值。
根据式(11)和(12)的计算可得，本构方程的计算值与实测流变应力值的平均相对误差仅为3.85%，且误差值都在10%以下。
4. 结论
1) Al-4.5Mg-0.6Mn铝合金峰值应力随应变速率的增大而增加，随着变形温度的升高而降低；真应力–应变曲线可以划分为加工硬化阶段、过渡阶段和稳态阶段3个部分；当变形温度为500℃，变形速率为10 s−1时，合金发生了动态再结晶。
2) 可以用包含Z参数的双曲正弦函数关系来描述Al-4.5Mg-0.6Mn铝合金高温变形时的流变应力行为，其材料常数A、α、n和Q分别为1.1336 × 1013、0.0102 MPa−1、6.1407和178.962 KJ/mol。
基金项目
广西科技计划项目(编号：桂科重14122001-5、1598001-2)。