1. 引言
在过去几年,许多农民采用农药控制、生物控制或者物理控制治理害虫。随着科技的发展,害虫治理有了更加合理的办法,如通过释放该害虫的自然天敌来遏制害虫的生长。最近,不少学者建立了具有脉冲害虫治理的捕食种群模型,并进行动态行为分析[1] -[9] 。Jiao等 [1] 建立了一类在不同脉冲时刻捕捞和释放的捕食-食饵模型,给出了害虫灭绝周期解的局部稳定性、全局稳定性和系统持久性的充分条件。Kunwer等 [2] 建立了不同年龄阶段天敌的三种群模型,获得了害虫灭绝周期解稳定性存在的充分条件和模型的持久性。Paul等 [3] 建立了一类在不同脉冲时刻脉冲扰动的植物害虫天敌模型,研究了模型正周期性的存在性以及稳定性存在的条件。
另一方面,现实世界中种群环境通常是随时间周期变化的,考虑具有周期系数模型更加符合实际。Yang [4] 建立了具有脉冲周期系数和Holling III类功能反应的捕食系统,并得到了系统的持续生存性、周期解的存在唯一性和全局吸引性。Liu等 [5] 研究了一类具有周期系数的单种群模型,得出了模型稳定性的条件。Tang等 [6] 研究了一类具有周期系数的捕食模型,获得了周期解稳定性的充分条件。
据作者所知,同时考虑在不同时刻进行收割庄稼、喷洒农药和释放天敌,并具有周期系数的捕食-食饵模型几乎未见报道,其动态性质研究显得非常重要。
本文建立了一类在不同脉冲时刻收割庄稼、喷洒农药和投放天敌,且具有周期系数的植物–害虫–天敌的脉冲控制模型如下:
 (1)
(1)
其中, 表示
表示 时刻植物的密度;
时刻植物的密度;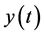 表示
表示 时刻害虫的密度;
时刻害虫的密度; 表示
表示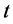 时刻天敌的密度。
时刻天敌的密度。 为植物的密度变化的内禀生长率,
为植物的密度变化的内禀生长率, 为植物的的环境容纳量函数,
为植物的的环境容纳量函数,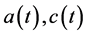 分别为植物和害虫的功能反应函数,
分别为植物和害虫的功能反应函数, 分别为植物和害虫的转化率及功能反应乘积函数,
分别为植物和害虫的转化率及功能反应乘积函数, 分别为害虫和天敌的死亡函数;其中
分别为害虫和天敌的死亡函数;其中 ,且都是
,且都是 周期函数;
周期函数; 表示释放天敌、喷洒农药和收割庄稼的周期;
表示释放天敌、喷洒农药和收割庄稼的周期; 表示
表示 时刻植物的收割率,
时刻植物的收割率, 分别表示
分别表示 时刻喷洒农药对害虫和天敌的损失率;
时刻喷洒农药对害虫和天敌的损失率; 表示
表示 时刻释放天敌的数量。
时刻释放天敌的数量。
我们主要利用线性化方法、脉冲微分方程的比较原理以及Floquet原理,讨论周期系统(1)的两个害虫灭绝周期解局部稳定性和全局稳定性的一些充分条件。
2. 预备知识
为了获得本文主要结论,本节将给出一些引理。
考虑脉冲微分方程
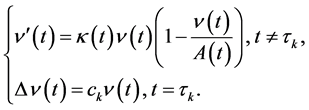 (2)
(2)
假设上述系统是T周期的,即存在 使得
使得
 (3)
(3)
且满足:
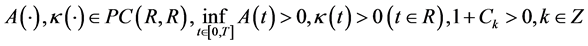 (4)
(4)
引理2.1 [10] 假设条件(3),(4)成立,若
 (5)
(5)
则系统有唯一的全局渐近稳定的正周期解 满足
满足 和
和 ,其中
,其中
 或者
或者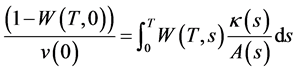 。
。
引理2.2 [11] 考虑如下的脉冲控制系统
 (6)
(6)
其中 。则系统有唯一的周期解
。则系统有唯一的周期解 ,且任意解
,且任意解 ,当
,当 有
有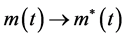 ,其中
,其中

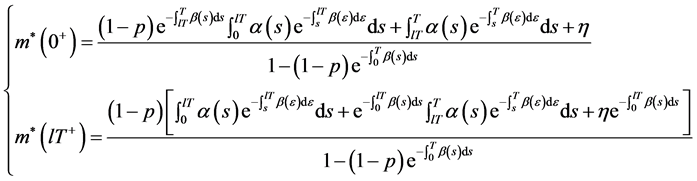
证明 由系统(6)有

利用系统(6)的第二个和第三个式子,我们得到
 (7)
(7)
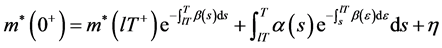 (8)
(8)
通过(7)和(8),有
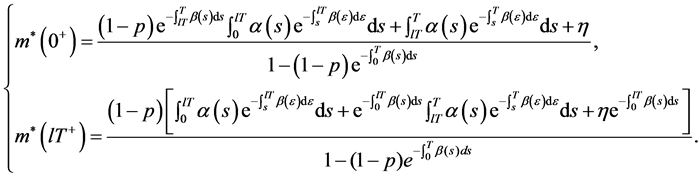
所以,可得系统(6)的周期解:

证毕。
3. 害虫灭绝周期解的稳定性
本节分析周期系统(1)的害虫灭绝的周期解的存在性,并给出周期解局部稳定性和全局稳定性的充分条件。
首先讨论系统(1)害虫灭绝周期解,即令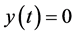 ,那么系统(1)将变为:
,那么系统(1)将变为:
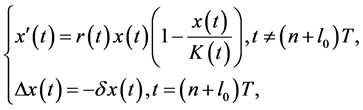 (9)
(9)
 (10)
(10)
根据引理2.1,如果

那么系统(9)有正周期解
 (11)
(11)
其中 。
。
利用引理2.2有系统(10)的周期解
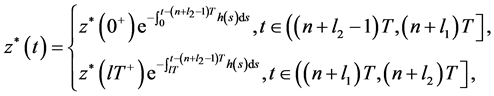 (12)
(12)
其中

由此可得系统(1)的两个害虫灭绝周期解 和
和 。下面我们分别讨论它们的稳定性问题。
。下面我们分别讨论它们的稳定性问题。
定理3.1 假设当 时,周期系统(1)的害虫灭绝周期解
时,周期系统(1)的害虫灭绝周期解 是局部稳定的;当
是局部稳定的;当 时,周期系统(1)的害虫灭绝周期解
时,周期系统(1)的害虫灭绝周期解 是不稳定的。
是不稳定的。
证明 假设 系统(1)的任意解,令
系统(1)的任意解,令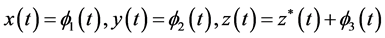 。将系统(1)在点
。将系统(1)在点 线性化得:
线性化得:
 (13)
(13)
设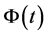 是系统(13)的基解距阵,则有
是系统(13)的基解距阵,则有

考虑系统(13)的脉冲部分,有

和

令

则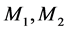 的系统乘子为
的系统乘子为
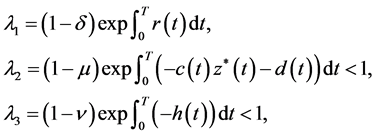
根据脉冲微分方程Floquet原理知,当 ,即
,即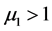 时害虫灭绝周期解
时害虫灭绝周期解 是局部稳定的。当
是局部稳定的。当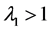 ,即
,即 时周期解
时周期解 是不稳定的。证毕。
是不稳定的。证毕。
下面我们讨论当 时,系统存在周期解
时,系统存在周期解 的稳定性。
的稳定性。
定理3.2 假设 ,如果
,如果
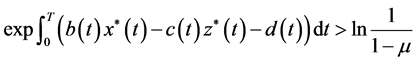 (14)
(14)
成立,则系统(1)的害虫灭绝周期解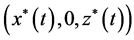 是不稳定的;如果
是不稳定的;如果
 (15)
(15)
成立,则系统(1)的害虫灭绝周期解 是局部稳定的。
是局部稳定的。
证明 类似定理3.1,将系统(1)在点 线性化的基解距阵有
线性化的基解距阵有
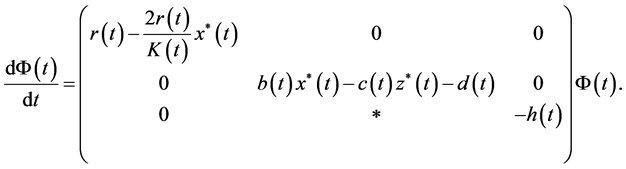
其中 且充分小。则
且充分小。则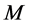 的系统乘子为
的系统乘子为

根据脉冲微分方程Floquet原理知,若 害虫灭绝周期解
害虫灭绝周期解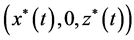 是不稳定的;若
是不稳定的;若 害虫灭绝周期解
害虫灭绝周期解 是局部稳定的。证毕。
是局部稳定的。证毕。
下面我们进一步得到 全局稳定性的充分条件。
全局稳定性的充分条件。
定理3.2 假设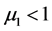 ,如果
,如果

成立,则系统(1)的害虫灭绝周期解 是全局渐近稳定的。
是全局渐近稳定的。
证明 假设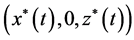 是系统(1)的任意解,则系统(1)可写作:
是系统(1)的任意解,则系统(1)可写作:
 (16)
(16)
由系统(16)第1个式子,得其比较系统
 (17)
(17)
由引理2.1和比较定理,有系统(17)存在周期解 且满足
且满足 当
当 ,其中
,其中 为方程(18)任意解。即存在整数
为方程(18)任意解。即存在整数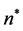 ,使得所有满足
,使得所有满足 ,且存在充分小的
,且存在充分小的 ,有
,有

类似地,考虑系统
 (18)
(18)
利用引理2.2,得系统(18)存在周期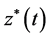 且满足
且满足 ,当
,当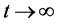 ,其中
,其中 为方程(18)任意解。
为方程(18)任意解。
即存在整数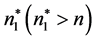 使得所有
使得所有 ,
,

从系统(1)的第二和第四个式子,我们得到
 (19)
(19)
那么

其中 。由脉冲的连续性,我们得频闪映射
。由脉冲的连续性,我们得频闪映射

其中 。
。
由条件 得
得 ,有
,有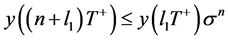 所以当
所以当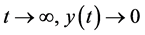 。因此存在一个充分小的
。因此存在一个充分小的 ,使得对所有的
,使得对所有的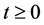 有
有 。
。
由系统(1),得到
 (20)
(20)
类似的,用比较原理和引理2.1,存在一个充分小的 且存在
且存在 使得
使得
 (21)
(21)
其中
同理我们可以得到
 (22)
(22)
类似的,存在一个充分小的 且存在
且存在 使得
使得
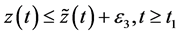
其中

不难得到当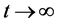 时,有
时,有 和
和 。证毕。
。证毕。
基金项目
国家自然科学基金(11471061);重庆市自然科学基金(No. CQ CSTC 2014JCYJA4004);重庆市高校创新团队计划(No. KJTD201308)。