Gale-Ryser型刻划定理的一个推广

A Generalization of the Gale-Ryser Type Characterization Theorem

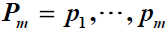
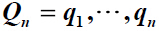
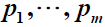
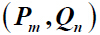
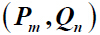
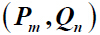
摘要: 设及 是两个由非负整数构成的不增序列。如果存在一个简单X，Y-二部图使得X中的顶点的度分别为 且Y中的顶点的度分别为 ，那么称序列对 是二部可图的。如果二部可图且任何两个来自不同部集的顶点之间最多连有t条边，那么称是t-二部可图的。本文给出一个t-二部可图序列的刻划定理。事实上，该定理是Gale-Ryser型刻划定理的一个推广。

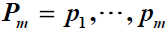
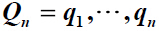
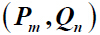
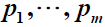
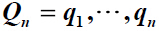
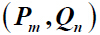
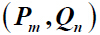
Abstract: Let and be two non-increasing sequences of nonnegative integers. The pair is said to be bigraphic if there is a simple X,Y-bigraph such that the vertices of X have degrees and the vertices of Y have degrees . is said to be t-bigraphic if it is bigraphic and no two vertices from different partite sets are joined by more than t edges. In this paper, we give a characterization for to be t-bigraphic. In fact, it is a gen-eration of the Gale-Ryser type characterization theorem.

1. 引言

设及是两个由非负整数构成的不增序列。如果存在一个简单-二部图使得中的顶点的度分别为且中的顶点的度分别为，那么称序列对是二部可图的。以下是著名的Gale-Ryser型关于二部可图序列的刻划定理。

定理1 (Gale [1] , Ryser [2] )设及是两个由非负整数构成的不增序列且满足条件，则序列对是二部可图的当且仅当对于任意的整数，，有

如果二部可图且任何两个来自不同部集的顶点之间最多连有t条边，其中t是正整数，那么称是t-二部可图的。本文给出一个t-二部可图序列的刻划定理。事实上，该定理是Gale-Ryser型刻划定理的一个推广，当时下面的定理2即为定理1。

定理2 设及是两个由非负整数构成的不增序列且它们满足条件，则序列对是t-二部可图的当且仅当对于任意的整数，，有

(1)

2. 定理2的证明

必要性。设是实现的一个t-二部图，其部集为和。考虑关联到中的个顶点的所有边。由于是t-二部图，因此每个最多关联到这些边中的条，而且也最多关联到这些边中的条。于是，是关联到的任意个顶点的所有边的条数的上界，这个界在度为的那些顶点上取得。

充分性。设有两个非增非负整数序列及，它们满足(1)式。首先，我们构造一个t-二部图，其部集和满足条件及。定义一个临界指标，它是满足条件且的最大的下标。我们将逐步去掉顶点处的差额而保持及。我们从个顶点的空图开始，此时，除非对于所有的都有，在这种情况下结论已成立。为了方便，记为顶点与之间的边所构成的集合，。对于顶点，由于，因此一定存在顶点使得。

情形(1) 对于某个和，，且存在某个使得。当时，在顶点与之间去掉一条边，在与之间连上一条边。当时，分别在与，与之间去掉一条边，分别在与，与之间连上一条边，其中。

情形(2) 对于某个和，且。当时，在与之间连上一条边。当时，在与之间去掉一条边，分别在与，与之间连上一条边，其中。

若以上两种情形均不能应用，则

由(1)知，又，故。重复上述步骤可得到图，满足且。又因为，从而有。因此就是想要的t-二部图，即是t-二部可图的。

基金项目

海南省自然科学基金资助项目(20151004)。