1. 引言
采用旋压工艺来生产各种贮箱封头(半球体壳体),其具有成形精度高、研制周期短等优点 [1] [2] 。旋压工艺分为强力旋压和普通旋压两种类型,强力旋压过程中毛坯的变形程度大。在旋压过程中,旋压成型工件能否符合预先规定的形状(即贴膜度大小),是旋压过程中重点考虑的因素。材料在旋压过程中经历复杂的多道次局部加载与卸载和不均匀变形,使得易出现形状尺寸精度低、环筋、金属堆积、壁厚过度减薄等缺陷 [3] ,严重影响工件的使用。
旋压过程中合适的工艺参数保证了较高的旋压件质量及尺寸精度。在铝合金半球壳体的旋压过程中,研究旋压成形的变形规律及工艺参数对旋压过程的影响,对理解半球体壳体的实际旋压操作有着重要的意义。文献中报道的有较多的旋压过程的数值模拟方面的研究 [3] - [8] ,例如吴统超等人对大型复杂薄壁壳体的第一道次旋压成形进行了分析 [3] ;吴松林等对气瓶旋压过程进行了模拟研究 [4] ;阴中炜等人以铝合金为材料进行了半球壳体的旋压成型工艺研究 [5] 。旋压过程中工艺参数的确定至关重要,不适当的工艺条件下,旋压件的尺寸精度差,其中旋压件与芯模之间的间隙(旋压间隙)不仅影响工件的尺寸精度及成型质量,同时对工艺过程中的变形有着非常重要的影响。旋压间隙对贴膜度的影响最大 [6] - [8] 。文献中报道的铝合金的半球壳体旋压研究里大多集中于工件的成型性及可能出现的缺陷进行分析研究 [2] [9] - [12] ,而较少关注旋压间隙对工件尺寸精度的影响以及对应力、应变变化规律影响程度。本文以铝合金为材料研究板料强旋过程中壁厚偏离(不同偏离率对应不同的旋压间隙)对金属变形以及应力分布规律的影响,通过对不同壁厚偏离率下的旋压过程模拟,研究旋压毛坯的变形规律,对减小旋压过程产生的金属堆积、形状尺寸精度低等缺陷具有积极的改善作用。
2. 建立模型
2.1. 模型描述
采用直径1200 mm、厚度20 mm铝合金板料,材质为2219退火态铝合金(模型中定义为弹塑性材料,杨氏模量为73,800 MPa,泊松比为0.33,密度为2.84 g/mm3)。利用大型非线性有限元软件SuperForm/Marc对半球壳体的旋压成形过程进行模拟。主要对三种旋压工况进行有限元模拟,壁厚偏离分别为0,−8%,+5%,三种工况分别对应不同的旋轮运动轨迹,分析其中的变形规律和特点,重点分析强旋过程的变形规律及壁厚偏离率对旋压的影响。
旋压过程是典型的三维变形问题,变形过程非对称,必须建立完整的旋压模型。旋压初始时模具的配置及尺寸如图1所示。旋轮攻角为30˚,在坐标第一象限,旋轮的圆角的初始坐标为(81.57, 509.26),半球形芯模半径476 mm,尾顶直径160 mm。在SuperForm中绘制旋轮、芯模及尾顶的型面,并在模型中将其设置为刚性面。旋轮和尾顶的旋转速度为60 r/mim。
为将单元数目控制在合理范围内,首先在板料径向断面(子午面)划分单元,径向划分60个单元,厚度方向划分3层单元,然后绕Y轴每2˚扩展180次得到3维实体单元,总单元数32,400。由于工件尺寸大,变形中细节上的变化(旋轮圆角、攻角等)对整体成形过程由明显影响,因此模型中单元尺寸不能太大,导致单元数目多。为提高分析速度,分为6个区进行并行计算,旋压过程视为350℃绝热变形。
2.2. 方案分析
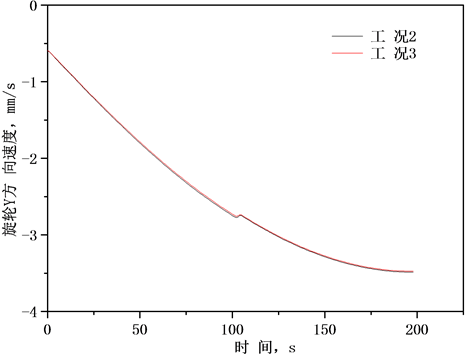
三种旋压工况的壁厚偏离分别为0,+5%,−8% (分别称为工况1、工况2、工况3)。不同工况下旋轮起始点坐标如表1所示。工况1的旋轮运动速度如图2所示,工况2和工况3对应的旋轮运动速度见图3。
3. 旋压过程中应力分化
由于法兰在旋压过程各点的轴向位移不尽相同导致法兰内产生一定的弹性变形,这种变形在旋转过程中还会发生不断的变化。弹性变形的变化会导致法兰内的应力变化,其中周向(环向)应力分量对法兰是否起皱失稳起直接影响,需要深入分析。

Figure 1. The mould setting when spinning is beginning
图1. 旋压开始时模具配置

Table 1. O1 coordinate of the spinningroller at different deviation rate conditions
表1. 不同厚度偏离率时旋轮O1点的坐标
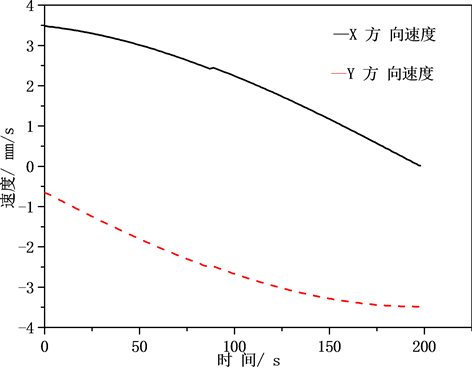
Figure 2. Linear velocities along X and Y direction (thickness deviation rate is 0)
图2. 旋轮在X、Y方向线速度(厚度零偏离)
 (a) (b)
(a) (b)
Figure 3. Spinning roller velocity at condition 2 and 3. (a) Linear velocities along X direction; (b) Linear velocities along Y direction
图3. 工况2和工况3下旋轮速度。(a) X方向速度;(b) Y方向速度
为了显示法兰在旋压过程的周向应力变化规律,以旋压24~25 s时间内(板料旋转1圈)法兰应力变化情况为例进行分析。
图4所示为旋压一圈过程中不同时刻法兰的周向应力分布(图中未显示已成型的壳体部分)。可见法兰在不同时刻,旋轮侧和芯模侧的周向应力分布明显不同。旋轮侧,靠近旋轮的部分区域分布明显周向压应力;而在芯模侧,靠近旋轮的部分区域分布明显周向拉应力,法兰的变形沿着芯模圆周展开,针对周向应力的变化,旋轮对法兰的加载作用在旋压过程中会传递到芯模侧,旋轮施加于法兰的压应力传递到芯模侧时则变成了拉应力,这种“外压内拉”的作用使得变形可以持续进行,从图4可以看出,法兰已变形区应力特点为旋轮侧受到拉应力,而芯模侧则承受压应力。
图5所示为旋压24 s时板料在各个方向上的应力分布。图中可以看出,已成型部分其残余应力分布特点:旋轮侧径向和周向受拉,而芯模侧径向和周向受压。由于内外层金属变形不均匀,变形过程中法兰外侧承受旋轮压应力,变形较大,内部变形相对较小,旋压导致的金属变形大,所以已经变形(成型)
 (a) (b)
(a) (b)  (c) (d)
(c) (d) (e) (f)
(e) (f)
Figure 4. The circumferential stress of flange when spinning is finished a circle. (a) The spinning roller side at 24 s; (b) The mandrel side at 24 s; (c) The spinning roller side at 24.59 s; (d) The mandrel side at 24.59 s; (e) The spinning roller side at 25.03 s; (f) The mandrel side at 25.03 s
图4. 旋压一圈过程法兰的周向应力分布(MPa)。(a) 24 s时旋轮侧;(b) 24 s时芯模侧;(c) 24.59 s时旋轮侧;(d) 24.59 s时芯模侧;(e) 25.03 s时旋轮侧;(f) 25.03 s时芯模侧
 (a) (b)
(a) (b)  (c) (d)
(c) (d)  (e) (f)
(e) (f) (g) (h)
(g) (h)
Figure 5. The stresses distribution when spinning at 24 s. (a) The radial stress at spinning roller side; (b) The radial stress at mandrel side; (c) The circumferential stress at spinning roller side; (d) The circumferential stress at mandrel side; (e) The axial stress at spinning roller side; (f) The axial stress at mandrel side; (g) The shearing stress on r-θ plane at spinning roller side; (h) The shearing stress on r-θ plane at mandrel side
图5. 旋压24 s时各向应力分布。(a) 径向应力旋轮侧;(b) 径向应力芯模侧;(c) 周向应力旋轮侧;(d) 周向应力芯模侧;(e) 轴向应力旋轮侧;(f) 轴向应力芯模侧;(g) r-θ平面内的剪应力旋轮侧; (h) r-θ平面内的剪应力芯模侧
的金属部分分布有较大的残余应力,其径、周向平面内分布明显的残余剪切应力(图5(g)、图5(h))。
4. 旋压过程中的变形分析
4.1. 零偏离率
以工况1 (零偏离率)为例,详细分析强旋过程的变形规律。图6所示为不同时间下工况1旋压过程中板料旋轮侧的等效变形分布。旋压过程中,变形以尾顶为中心,变形相四周均匀扩展,随着旋轮的进给,变形逐渐增大,旋压成形的壳体厚度逐渐减薄,变形呈一定梯度的同心圆分布。旋轮处法兰承受的力最大,相应的变形也最大,即应变量也最大。由于是高温(350℃)绝热条件,铝合金板料的塑形好,在强旋阶段,变形主要在法兰内径处,无金属堆积、环筋等质量缺陷现象,所以法兰的外径基本不变,无变形。在旋压60 s时(图6(b)),板料最大等效应变量约为4.0。
图7所示为工况1旋压过程中板料径向断面的变形分布及形状。可见,半球壳旋压过程中,旋轮侧的变形显著大于芯模侧。前50 s (图7(a)、图7(b))旋压过程中,板料法兰基本保持平直。在60 s (图7(c))时,法兰向前明显倾斜。理论上,在壳体厚度零偏离率下,旋轮运动轨迹按板料壳体正弦规律减薄,能够保证法兰的平直。然而实际情况是当零偏离旋压到一定程度时,已成形的壳体不能很好贴模,使得已成形的实际金属体积大于理论所需量,旋轮变形区中的外表面金属被拉向球壳,在旋轮接触处形成塑性铰,导致了法兰前倾现象。
为了对旋压过程中壳体的贴模进行量化分析,在板料内侧沿径向取A~E共5个节点,如图8(a)所示。根据各节点在旋压过程中的初始坐标及位移量可计算出这些点距半球壳球心的距离。旋压过程中,各点依次贴向芯模。贴模后,距心部距离保持为芯模半径。成形后这些点不能贴模则其距球心距离与芯模半径存在偏差,称为间隙量。由图8(b)、图8(c)可见,在旋压30 s后,B点和C点开始与芯模脱离,在随后的旋压过程中间隙逐渐增大,旋压到60 s时,间隙增加到1.3 mm。

 (a) 10 s (b) 60 s
(a) 10 s (b) 60 s
Figure 6. The effective strain distribution at condition 1
图6. 工况1强旋过程等效应变分布(旋轮侧)
 (a) 30 s
(a) 30 s  (b) 50 s
(b) 50 s (c) 60 s
(c) 60 s
Figure 7. The fault plane shape and deformation distribution at condition 1
图7. 工况1旋压过程中板料断面形状及变形分布
4.2. +5%偏离率
工况2旋压时,旋轮运动轨迹按壳体目标厚度的+5%设定。强旋过程中不同时刻断面的形状及变形分布如图9所示。变形的分布规律与工况1基本相同,但相比于工况1变形量稍小。旋压前50 s (图9(a)、图9(b)),法兰保持平直状态,而当旋压进行到60 s (图9(c))时,法兰已经明显前倾。
 (a)
(a) 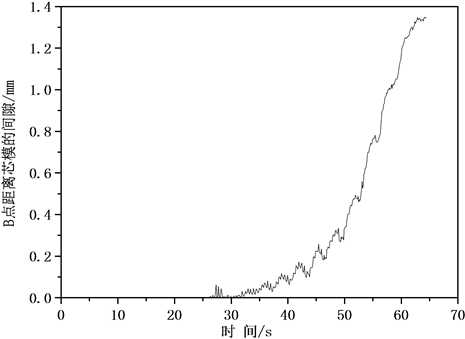
 (b) (c)
(b) (c)
Figure 8. The fittability at condition 1. (a) The location of 5 points; (b) The distance between different point and the centre of sphere; (c) The gap space between B and the mandrel
图8. 工况1旋压过程贴模情况。(a) 各点位置;(b) 各点距球心距离;(c) B点与芯模间隙
 (a) 30 s
(a) 30 s  (b) 50 s
(b) 50 s (c) 60 s
(c) 60 s
Figure 9. The fault plane shape and deformation distribution at condition 2
图9. 工况2旋压过程断面形状及变形分布
图10所示为工况2旋压下过程中的贴模情况分析。50 s (如图10(b))时其贴模情况变差,但相对于工况1,B点与芯模的间隙量相对较小。
4.3. −8%偏离率
在工况3旋压过程中,旋轮运动轨迹按壳体目标厚度的−8%设定。强旋过程中不同时刻断面的形状及变形分布如图11所示。由于采用的是负偏离率旋压,旋压出的壳体变形大于前两种工况。旋压开始时,旋轮即给板料一定压下量,导致板料内侧对应位置处也有较大变形。从旋轮位置处,多余的金属流向法兰,由于过多的金属从板料外侧流向法兰,在已成形的壳体与法兰交界处存在一个环形的凸出,使得法兰向后倾斜(即倾向芯模侧),如图11所示。
图12所示为工况3旋压下过程中的贴模情况分析。当旋压进行到30 s (如图12(b))时其贴模情况开始变差,相对于工况2,B点与芯模的间隙量相对增大。
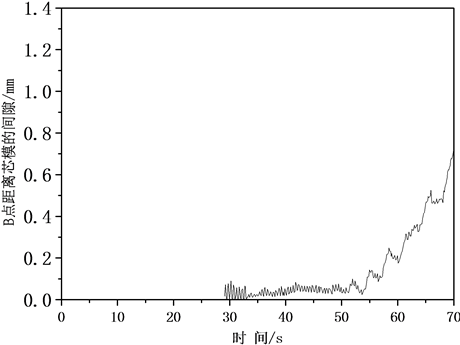
 (a) (b)
(a) (b)
Figure 10. The fittability at condition 2. (a) The distance between different point and the centre of sphere; (b) The gap space between B and the mandrel
图10. 工况2旋压过程贴模情况。(a) 旋压过程中各点距球心距离;(b) B点在强旋过程与芯模间的间隙
 (a) 30 s
(a) 30 s (b) 50 s
(b) 50 s
Figure 11. The fault plane shape and deformation distribution at condition 3
图11. 工况3旋压过程板料断面形状及变形分布
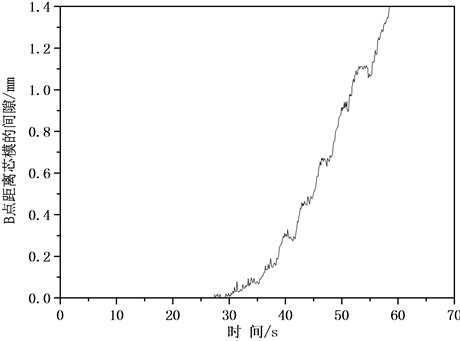
 (a) (b)
(a) (b)
Figure 12. The fittability at condition 3. (a) The distance between different point and the centre of sphere; (b) The gap space between B and the mandrel
图12. 工况3旋压过程贴模情况。(a) 旋压过程中各点距球心距离;(b) B点在强旋过程与芯模间的间隙
5. 结论
1) 旋压过程中,法兰的应力分布具有明显的规律。板料外侧,靠近旋轮的部分区域分布明显周向压应力;板料内侧,靠近旋轮的部分区域分布明显的周向拉应力。靠近旋轮的金属在旋转到旋轮变形区时周向应力较大;一旦金属成型后,周向应力在较小范围内波动;远离旋轮变形区的法兰金属周向应力较小,在−5~2 MPa范围内变化。从上述应力分析可知,法兰如果起皱失稳,是从旋轮附近金属开始。
2) 旋压过程中板料变形随着壁厚减薄率增加而增加,外层变形呈台阶状增加;同一变形时刻,变形大小顺序:负偏离 > 零偏离 > 正偏离。
3) 根据模拟计算结果,三种工况下壳体都不能很好贴模。但不同的偏离率对壳体贴模情况影响很大,对应大尺寸半球壳体的旋压成形贴模性好坏顺序为:正偏离 > 零偏离 > 负偏离。成形后的壳体厚度越大其贴模性越好。
4) 工况3 (偏离率−8%)从旋压开始,法兰就开始向后倾斜,且倾斜角度逐渐增大;而工况1 (零偏离)和工况2 (+5%偏离率)在旋压55 s之前,法兰都基本保持平直,随后法兰逐渐向前倾斜。工况1由于贴模性最差,在后期的旋压中,法兰前倾变化速度较快。