1. 引言
广义积分 与
与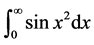 称为Fresnel积分 [1] ,它是以法国土木工程师兼物理学家Fresnel命名。Fresnel积分是物理光学衍射中常用的典型积分。它当今国际上的重大前沿基础科研领域–惯性约束聚变 [2] 、粒子场测试及在数字全息领域,如“形貌测量、变形测量、防伪、三维图像识别、医学诊断、数字全息显微 [3] 、去除数字全息零极像 [4] ”等方面有广泛的应用。因此对Fresnel积分进行推广是很有必要的。
称为Fresnel积分 [1] ,它是以法国土木工程师兼物理学家Fresnel命名。Fresnel积分是物理光学衍射中常用的典型积分。它当今国际上的重大前沿基础科研领域–惯性约束聚变 [2] 、粒子场测试及在数字全息领域,如“形貌测量、变形测量、防伪、三维图像识别、医学诊断、数字全息显微 [3] 、去除数字全息零极像 [4] ”等方面有广泛的应用。因此对Fresnel积分进行推广是很有必要的。
定义1.1 [5] 设 是定义在
是定义在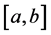 上的一个函数,
上的一个函数, 是一个确定的实数。若对任给的正数
是一个确定的实数。若对任给的正数 ,总存在某一正数
,总存在某一正数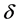 ,使得对
,使得对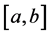 的任意分割
的任意分割 ,以及在其上任意选取点集
,以及在其上任意选取点集 ,只要
,只要 ,就有
,就有
 ,
,
则称函数 在区间
在区间 上可积(或黎曼可积);数
上可积(或黎曼可积);数 称为
称为 在
在 上的定可积(或黎曼积分),记作
上的定可积(或黎曼积分),记作
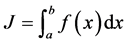 。
。
其中被积函数为 ,积分变量为
,积分变量为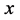 ,积分区间为
,积分区间为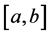 ,定积分下限和上限分别为
,定积分下限和上限分别为 。
。
定义1.2 [5] 设定义在无穷区间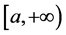 上的函数
上的函数 在任何有限区间
在任何有限区间 上都可积。如果存在极限
上都可积。如果存在极限
 ,
,
那么称此极限 为函数
为函数 在
在 上的无穷限反常积分(简称无穷积分),记为
上的无穷限反常积分(简称无穷积分),记为
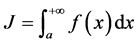 ,
,
并称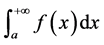 收敛。
收敛。
定义1.3 [6] 含参量积分 称为伽马函数(
称为伽马函数(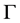 函数)。
函数)。
定义1.4 [7] 设有曲线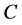 :
:
 ,
, 。
。
以 为起点,
为起点, 为终点,
为终点, 沿
沿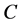 有定义。沿着
有定义。沿着 从起点
从起点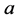 到终点
到终点 的方向在
的方向在 上取分点:
上取分点:
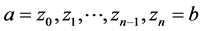 。
。
把曲线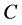 分成若干个弧段
分成若干个弧段

在 到
到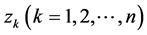 的每一段弧上任取一点
的每一段弧上任取一点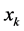 。作成和数
。作成和数
 ,
,
其中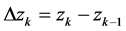 。当分点无限增加时,这些弧段长度的最大值趋于0,如果和数
。当分点无限增加时,这些弧段长度的最大值趋于0,如果和数 的极限存在且等于J,那么称
的极限存在且等于J,那么称 沿C (从a到b)可积,并称J为
沿C (从a到b)可积,并称J为 沿C (从a到b)的积分,并用记号
沿C (从a到b)的积分,并用记号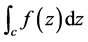 来表示:
来表示:
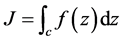 。
。
其中C称为积分路径。
定义1.5 [7] 整函数是指在整个复平面上都解析的函数。
定理1.
 ,
,
 。
。
2. 引理
为了证明定理1,需要如下引理。
引理3.1 (约当不等式) [8] 当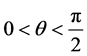 时,有
时,有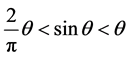 。
。
引理3.2 [5] 若 与
与 都收敛,
都收敛,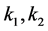 为任何常数,则
为任何常数,则
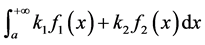
也收敛,且
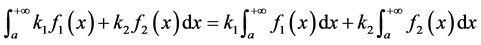 。
。
引理3.3 [5] 若函数f在 上可积,那么
上可积,那么 在
在 上也可积,且
上也可积,且
 。
。
引理3.4 [7] 设 沿曲线C连续,
沿曲线C连续,
 ,
,
其中C由曲线 和
和 衔接而成。
衔接而成。
引理3.5 [7] 设(1) 在单连通区域
在单连通区域 内连续;(2)在区域
内连续;(2)在区域 内
内 沿任一围线的积分值都为0。若
沿任一围线的积分值都为0。若 为
为 在单连通区域
在单连通区域 内的任一原函数,则有
内的任一原函数,则有
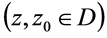
 。
。
引理3.6 (柯西积分定理) [9] 被积函数 在单连通区域
在单连通区域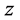 平面上处处解析,它沿
平面上处处解析,它沿 平面上任何闭曲线的积分为0。
平面上任何闭曲线的积分为0。
引理3.7 (Gamma函数的递推公式) [6]  ,
, 。
。
引理3.8 (余元公式) [10]  。
。
特别的,
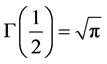 。
。
3. 定理的证明
证明 设辅助函数
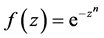 ,
,
它是一个整函数。并取如下图的辅助积分路径 。
。

记 ,
,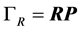 由引理1 (柯西积分定理),得
由引理1 (柯西积分定理),得
 。 (1)
。 (1)
首先考虑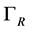 上的积分,记
上的积分,记
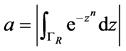 ,
,
因而
 。
。
由引理3.3,得
 。
。
令
 ,
,
则
 。
。
由引理3.1和引理3.5,得
 。
。
当 时,有
时,有
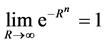 ,
,
因而
 。
。
因此当 时,有
时,有
 。
。
令 ,有
,有
 。
。
得

由定义1.3,得
 。
。
令
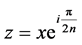 ,
,
则
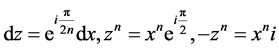 ,
,
有
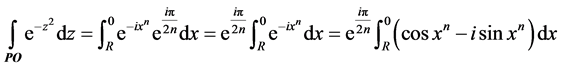 ,
,
当 时,(1)式变成
时,(1)式变成
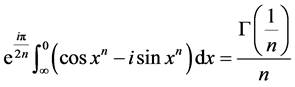 ,
,
整理得

两个代数形式相同的复数,它们的实部和虚部都要对应相等,即得
 ,
,
 。
。
注:当 时,结论变为
时,结论变为
 ,
,
 ,
,
这就是熟知的Fresnel积分,因此本结论Fresnel积分的一种推广。
*通讯作者。