1. 引言
陀螺仪是惯性导航系统的重要元件之一，其主要用途是用它来测量运动物体的角速度。随着对于惯导系统精度要求的不断提高，陀螺仪的精度要求也同样提高 [1] 。这样，传统的重力场下1 g作为输入对于陀螺仪漂移率系数的标定方法已经不能满足标定精度要求，且不能给予足够的加速度输入激励出高次漂移率系数。离心机可以依靠旋转时产生的向心加速度提供陀螺仪较高的输入比力，因此，可以采用离心机试验对陀螺仪的高次项漂移率系数进行标定。但是，在应用离心机进行陀螺仪参数标定时，其自身的误差往往会影响陀螺仪的标定精度，随着对于陀螺仪精度的要求越来越高，离心机误差对于陀螺仪参数标定精度的影响势必要进行着重分析，从而满足标定精度 [2] - [4] 。本文提出了一种带有反转平台的盘式离心机标定陀螺仪参数的方法。结合该离心机分析了其可能存在的各误差源，通过建立坐标系，并应用齐次变换的方法推导出了陀螺仪标定时误差影响较大的角速度输入的精确表达式，同时给出了陀螺仪各轴的比力输入表达式。通过特殊位置获得陀螺仪输出并结合已推导出的角速度输入、比力输入表达式以及陀螺仪静态误差模型，可以得出各项漂移率系数的表达式，从而通过误差补偿，提高标定的精度。
2. 带有反转平台的离心机及其误差源
应用离心机进行陀螺仪测试时，离心机旋转角速度会使陀螺仪产生牵连运动，从而在陀螺仪外环轴方向产生附加的陀螺干扰力矩，使得陀螺仪的输出存在偏差。为了消除这一影响，选用带有反转平台的离心机，它仅提供大的加速度输入，且相对惯性空间的角速率几乎为0。如图1所示。
图1为盘式离心机的侧视图，其中，“A”表示盘式离心机主轴，“B”表示反转平台回转轴，试验过程中，理想状态下主轴的旋转角速度矢量为
，反转平台角速度矢量为
，二者大小相等，方向相反。为了便于标定陀螺仪的漂移误差系数，在反转平台上安装一个可绕“C”轴旋转的平台，其旋转角度为
，试验时反转平台上固连的各部件所受的向心加速度处处相等 [4] 。
由文献 [1] 可知，若不考虑速率台作用，离心机输入加速度分解到陀螺仪输入轴方向的加速度大小为：
(1)
其中，
为开始测试时陀螺仪输入轴与向心加速度a方向之间的初始相位角。
采用精密离心机对陀螺仪的漂移率系数进行标定时，离心机自身的误差会影响标定的精度。这里，通过对离心机各误差源的分析，建立与误差相应的坐标系，并用齐次变换将位姿误差进行传递，可以得出各误差源对陀螺仪漂移率系数计算精度的影响。图2给出了离心机上建立的各坐标系，其中，坐标系o0x0y0z0为地理坐标系，o1tx1ty1tz1t为主轴轴套坐标系，o1x1y1z1为主轴坐标系，o2tx2ty2tz2t为反转平台回转轴轴套坐标系，o2x2y2z2为反转平台回转轴坐标系，o3tx3ty3tz3t为速率台轴轴套坐标系，o3x3y3z3为速率台坐标系，o4x4y4z4为工作基面坐标系，o5x5y5z5为陀螺仪坐标系。
表1给出了离心机上与各坐标系相关的位姿误差项以及其相应的齐次变换式。其中，Dqx1t、Dqy1t为主轴轴套的安装误差角；Dqx1(Wt)、Dqy1(Wt)为主轴倾角回转误差；Dqy2t、Dqx2t为反转平台回转轴与盘面的垂直度误差；Dqx2(−Wt)、Dqy2(−Wt)为反转平台回转轴倾角回转误差；Dqx3t、Dqz3t为速率台轴线与反转平台回转轴轴线的垂直度；Dqx3(wt)、Dqz3(wt)为速率台回转轴倾角回转误差；Dqx4、Dqz4为工作基面与反转平台回转轴轴线的垂直度；Dqx5、Dqz5为陀螺仪安装基面姿态误差，Dqy5为陀螺仪安装初始对零误差。
3. 陀螺仪的静态误差模型
陀螺仪静态误差模型的一般形式为：
(2)
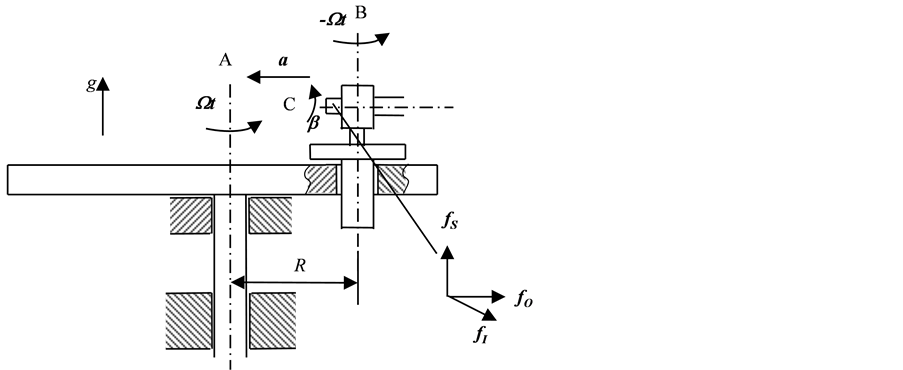
Figure 1. Schematic figure of disk centrifuge with counter-rotating platform
图1. 带有反转平台的盘式离心机的示意图
Figure 2. Coordinate systems of precision centrifuge
图2. 精密离心机坐标系
Table 1. Corresponding coordinate systems about errors of centrifuge and their homogeneous transformations
表1. 离心机误差项相关坐标系及其齐次变换式
其中，
为陀螺仪的角速率当量输出，单位为˚/h；
为沿陀螺仪输入轴方向的角速率；
为与加速度无关的漂移率，单位为˚/h；
、
、
分别为沿陀螺仪输入轴IA、输出轴OA和自转轴SA的比力分量；
、
、
分别为沿IA、OA、SA轴加速度引起的漂移率系数，单位为˚/h/g；
、
、
分别为沿IA、OA、SA轴的加速度二次方引起的漂移率系数，单位为˚/h/g2；
、
、
分别为沿IA和OA轴、IA和SA轴、OA和SA的加速度的乘积引起的漂移率系数，单位为˚/h/g2；
为残余误差 [5] - [7] 。
4. 离心机误差源对陀螺仪输入角速度、输入比力的影响
由于陀螺仪主要是敏感运载物体相对于惯性空间的角速度，角速度用来提供运动物体的角速度，因此，角速度输入量的精确与否对于陀螺仪的标定至关重要。应用离心机对陀螺仪进行标定时，离心机的姿态误差影响陀螺仪相对惯性空间的输入角速率
。在反转平台运动的情况下，参见图2的坐标系，考虑姿态误差对于陀螺仪输入角速度的影响，可以得到相应的角速度沿陀螺仪坐标系各轴的表达式为：
(3)
经计算，并忽略掉高阶无穷小量得：
(4)
取
。这样，陀螺仪输入轴相对于惯性空间的角速度为：
(5)
其中：
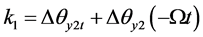
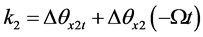
为反转平台角速率与主轴角速率的大小之差，
为地球自转角速度，
为当地纬度。
离心机的误差同样影响着陀螺仪各轴的输入比力的精度，但是由于比力引起的陀螺仪漂移系数本身就很小，且精密离心机的误差一般为10−5量级，对于陀螺仪的输出影响很小，可以忽略不计，因此这里对于离心机误差对陀螺仪各轴输入比力的影响不做过多研究，只给出陀螺仪各轴输入的标称值。考虑旋转物体受到哥式加速度的影响得：
(6)
(7)
(8)
其中，
；
，
为半径的标称值。
5. 离心机对陀螺仪漂移率系数的标定方法
将式(5)、(6)、(7)、(8)代入式(2)中，整理可得：
(9)
其中：
(10)
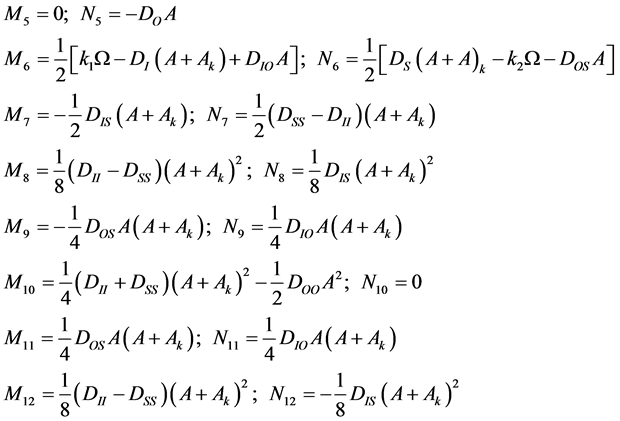
从式(9)中可以看出，陀螺仪输出中可以包含1~12次谐波成分，若利用谐波分析法最多需要辨识25
个谐波幅值，为了降低需辨识谐波幅值的个数，简化谐波分析的过程，分别取
，即绕“C”
轴旋转平台处于上述四个角位置时进行试验标定。将上述
值分别代入式(9)可知，陀螺仪的输出只包含常数项，一次余弦项，一次正弦项，二次余弦项，二次正弦项等5项谐波成分，即只需辨识5个谐波幅值，表2给出了
取不同值时，陀螺仪各谐波幅值的表达式。
进而式(9)可以简写为：
(11)
试验前，初始安装陀螺仪时，使陀螺仪的输入轴方向与向心加速度方向相重合，并将该位置设置为起测零点，这样采用寻零起始采样的方法，可保证在采样初始时刻
，进而设置绕“C”轴旋转平台的角位置；试验时，保持其角位置不变即该平台不进行转动，通过运转主轴与反转平台产生比力输入与角速率输入，以等时间间隔记录下反转平台旋转整周各采样时刻的陀螺仪输出。待绕“C”轴旋转平台的四个角位置全部进行数据采样后，应用谐波分析法分别计算出四组共20项谐波幅值，再令：
(12)
根据表2和式(10)可以得出
与陀螺仪各漂移系数的关系为：
(13)
其中，
，
为结构矩阵，
为包含离心机误差项、地球自转角速率等的常值向量。
这样利用最小二乘估计可得漂移系数向量为：
(14)
通过式(14)即可计算出陀螺仪各漂移系数的值，并且由于包含了离心机误差项，相当于对于标定结果进行了误差补偿。
Table 2. Expression of each harmonic amplitude of gyro changed by b
表2. b不同取值时陀螺仪各谐波幅值的表达式
试验研究发现，上述方法在采用单一基频的情况下可以有效的辨识
、
、
三个漂移系数，且可以保证较高的辨识精度，但是对于其他漂移系数不能满足辨识精度要求，因此，这里采用双球面试验方法，即由离心机分别两次提供不同的向心加速度进行试验标定。两次试验分别获得两组陀螺仪输出，根据公式(11)利用谐波分析法可以计算出两组数据各谐波的幅值
和
。将两幅值向量组合为：
(15)
同样根据公式(10)可以得出两组结构矩阵
、
，合并结构矩阵为：
(16)
这样，再利用公式(14)计算各漂移系数的数值，可以有效保证所有漂移系数的辨识精度。
6. 试验仿真与误差分析
下面通过具体的仿真算例来验证该方法的有效性，设如图1所示的某盘式离心机半径R0为1 m，试验所在地的纬度
为N45.75˚，取离心机各姿态误差量级均为1 × 10−5 (10−5 rad = 2.063)。试验时，将输出精度为10−3˚/h的某型号陀螺仪固定于速率台上，分别设置绕“C”轴旋转平台的4个角位置，每个角位置下，同时运转主轴和反转平台，其中，主轴与反转平台的转速大小相等，方向相反。试验过程中，离心机分别提供10 g与20 g大小的比例输入，相当于主轴分别提供W为10 rad/s，14 rad/s的角速度。以每2p/36的时间间隔进行数据采集，反转平台回转一周数据采集完毕，这样可以获得两组共72个数据。已知该陀螺仪的部分漂移系数为DF = 0.9043˚/h，DI = 1.5365˚/h/g，DO = 0.7431˚/h/g，DF = −0.0221˚/h/g。将采样获得的数据代入公式(11)，应用谐波分析法可求得如表3所示的各谐波幅值。
需要指出的是，一般陀螺仪的输出为^/s，这里结合陀螺刻度因数(^/˚)将其输出转化为表中给出的单位˚/h所对应的数值。
应用公式(12)将表3所示的谐波幅值进行组合成，同样根据表2和式(10)得出结构矩阵，并应用式(17)进行组合，利用公式(14)计算各次漂移系数分别为：
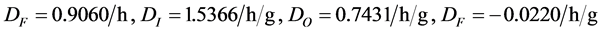
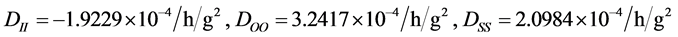
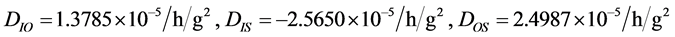
Table 3. Values of each harmonic amplitude of gyro outputs at two different rotating rates of the main axis
表3. 两次主轴转速下的陀螺仪输出各谐波幅值
将上面的计算结果同已知的陀螺仪漂移系数进行对比可以看出，该方法可以有效的标定陀螺漂移系数，且满足精度要求。同时该方法可以标定出高次项陀螺漂移系数，为陀螺仪高g条件下工作实现精确输出打下基础。
通过上面的公式推导以及试验仿真分析可以发现，采用带反转平台的离心机进行陀螺仪标定时，能够影响陀螺仪漂移系数的离心机自身误差项很少，从公式(10)可以看出，只有反转平台回转轴与盘面的垂直度误差Dqy2t、Dqx2t，反转平台回转轴倾角回转误差Dqx2(−Wt)、Dqy2(−Wt)以及反转平台角速率与主轴角速率的大小之差
会对系数标定结果产生影响，这说明采用此测试方法可以有效的规避离心机误差带来的影响，从而为精度不高的离心机标定陀螺仪提供了一定的理论基础。
以误差项Dqy2t为例，分析其对于各漂移系数标定精度的影响，若常值向量矩阵
中只包括Dqy2t项误差，分析其单独作用下该误差对于各系数的影响，由公式(14)可得：
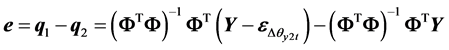
经计算可知Dqy2t对于漂移系数DI、DS的标定精度影响较大，影响大小分别为1.5143˚/h/g、−0.0418˚/h/g2，对于其他的漂移系数几乎无影响。从分析结果可知，Dqy2t对于漂移系数的影响程度非常大，甚至可以超过了标定结果几个量级的大小，这说明采用离心机进行陀螺仪标定时，要高度重视误差带来的影响，若上面的试验不考虑离心机误差项的话，即用公式
进行计算可得标定结果其中DI = −1.5268˚/h/g，可见与真实值偏离较远。这一点从单位换算推导中也可以看出，如式(5)中，以试验中的离心机误差10−5 rad为例，
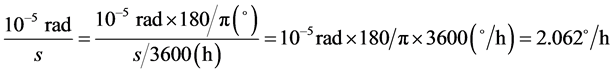
而且误差为10−5 rad (2.063)的离心机已经属于精密离心机，更加说明标定时考虑离心机误差的重要性。
同理可以计算Dqx2t的影响，经计算其影响DI、DOS两项漂移系数，分别影响大小为−0.0429˚/h/g以及−0.0182˚/h/g2。分析反转平台角速率与主轴角速率的大小之差
可得其对于DI漂移系数的影响为−0.0511˚/h/g。综上，上述试验结果正是在考虑了离心机误差的基础上才能满足标定精度要求，试验证明了采用离心机进行陀螺仪漂移系数标定时，必须要考虑离心机误差的影响。
7. 结论
本文在带反转平台的离心机上建立坐标系，分析了各坐标系下存在的误差源，给出了含误差项的陀螺仪相对惯性空间角速率输入及各坐标轴实际输入比力的标称值。给出了陀螺仪速率法标定陀螺仪漂移系数的方法，根据公式(9)~(14)可以计算得出各漂移系数大小。
试验仿真表明采用本文设计的试验方法可以有效的规避离心机误差。其中，离心机误差只对于DI、DS和DOS的标定有影响，且影响非常大，须在考虑离心机误差的情况下才能够实现精确标定；对于其他系数标定没有影响。实际标定时需要精确测量反转平台回转轴与盘面的垂直度误差，反转平台回转轴倾角回转误差以及反转平台角速率与主轴角速率的大小之差等以满足标定精度要求。
基金项目
天津科技大学青年教师创新基金2015LG03。