1. 引言
近年来,无人直升机由于其独特的优势如价格低、噪声小、可以垂直起飞和降落、机动灵敏,在农业领域、军用领域和娱乐领域等方面得到了普遍的应用 [1] 。但是由于无人直升机的控制系统具有高度的复杂性和强耦合性 [2] ,所以如何实现无人直升机的稳定控制是无人机学术研究领域所面临的挑战。
目前很多国内外研究者对直升机的控制进行了研究,例如文献 [3] 运用了滑模控制方法来跟踪直升机的轨迹,对系统进行内外环仿真,提高系统的动态性能。文献 [4] 讲了卡尔曼滤波和直升机自主着陆的相关性,证明了直升机可以实现稳定、灵活、无误差的飞行。文献 [5] 在直升机模型中运用线性二次型调节器来实现控制系统所需的性能。文献 [6] 主要是解决了直升机在飞行过程中遇到的风力等外界的影响,通过直接反馈同步设置和状态观测提高了系统的鲁棒性,预估并减小不确定性因素。文献 [7] 运用神经网络模型实现系统的姿态跟踪。为了实现系统的稳定性和抑制风力等干扰因素,实现系统的可靠性飞行,本文采用闭环控制的方法。
本文以X-Cell 60 SE直升机为研究平台,详细介绍了模型直升机的动力学方程,将各个因素考虑在内,并且将PID闭环控制方法应用在模型直升机的建模中,使系统能够快速响应,消除外界风力干扰等产生的误差,达到轨迹跟踪的目的,通过Simulink仿真验证了控制系统的有效性。
2. 模型直升机动力学模型
模型直升机的装置有主旋翼、稳定杆、尾桨、垂尾和平尾等,主旋翼主要是提供模型直升机所需升力和扭矩,稳定杆的作用是作为主旋翼的稳定装置,提高系统的稳定性,尾桨的作用是提供偏航力矩,并且与主旋翼产生的反扭矩相抵消,控制模型直升机的航向,垂尾和平尾作为稳定装置来提高整个系统的稳定性,建立的坐标系如图1 [8] 。
在无人机飞行力学中,假设机体坐标系与地面坐标系之间的欧拉角为 ,根据刚体运动的牛顿-欧拉方程可得到模型直升机的相关方程。
,根据刚体运动的牛顿-欧拉方程可得到模型直升机的相关方程。
 (1)
(1)
 (2)
(2)
 (3)
(3)

Figure 1. Model helicopter coordinate frame system
图1. 模型直升机坐标结构图
 (4)
(4)
 (5)
(5)
 (6)
(6)
在上式中,公式(1)为平移方程,公式(2)为转动方程,公式(3)为导航方程,公式(4)为姿态方程,公式(5)(6)为旋翼挥舞方程, 为线速度,
为线速度, 为角速度,
为角速度, 为欧拉角,
为欧拉角, 为位置信息,
为位置信息, 为旋翼挥舞角,
为旋翼挥舞角, 为模型直升机三个方向的受力情况,
为模型直升机三个方向的受力情况, 为三个方向的力矩,
为三个方向的力矩, ,
, 表示挥舞角的变化量,计算公式为
表示挥舞角的变化量,计算公式为 ,
, 表示稳定性导数,旋翼挥舞阻尼时间常数
表示稳定性导数,旋翼挥舞阻尼时间常数 为
为 ,
, 、
、 是从舵机输入到主旋翼挥舞角的纵向和横向增益 [9] 。
是从舵机输入到主旋翼挥舞角的纵向和横向增益 [9] 。
2.1. 受力分析
模型直升机非常复杂,受力情况包括主旋翼、尾桨、平尾、垂尾和机身所受的力,即 ,分析如下。
,分析如下。
1) 主旋翼受力情况:要计算模型直升机的主旋翼产生的拉力,首先要分析主旋翼的拉力系数,即
 (7)
(7)
所以可得到,
 (8)
(8)
主旋翼的拉力系数 以及入流比
以及入流比 的计算方法,可以通过不断进行迭代,运用动量理论来实现,如下:
的计算方法,可以通过不断进行迭代,运用动量理论来实现,如下:
 (9)
(9)
 (10)
(10)
 (11)
(11)
 (12)
(12)
其中, 为模型直升机的前进比,
为模型直升机的前进比, ,
, 为模型直升机的垂向比,
为模型直升机的垂向比, ,
, 为大气密度,
为大气密度, 为主旋翼的速度,
为主旋翼的速度, 为主旋翼的半径,
为主旋翼的半径, 是非理想尾流收缩系数,
是非理想尾流收缩系数, 为主旋翼升力曲线斜率,
为主旋翼升力曲线斜率, 为主旋翼实度,
为主旋翼实度, ,其中,
,其中, 为桨叶片数,
为桨叶片数, 为桨叶宽 [10] ,对于本文研究的模型直升机,
为桨叶宽 [10] ,对于本文研究的模型直升机, ,
, 是总距角,其计算公式为
是总距角,其计算公式为 。
。
下面求解主旋翼的反扭力矩,求解公式 [5] 为
 (13)
(13)
根据扭矩系数可得到主旋翼的反扭力矩为
 (14)
(14)
其中, 为主旋翼桨叶的侧向阻力系数,求得的值为
为主旋翼桨叶的侧向阻力系数,求得的值为 ,
, 为主旋翼反扭矩。
为主旋翼反扭矩。
2) 尾桨受力情况:尾桨受力的计算方法与主旋翼的计算方法类似,如下:
 (15)
(15)
 (16)
(16)
其中, 是尾桨的拉力系数,
是尾桨的拉力系数, 是尾桨的转速,
是尾桨的转速, ,
, 是尾桨到主旋翼的传动比,
是尾桨到主旋翼的传动比, ,
, 是尾桨半径。
是尾桨半径。
 (17)
(17)
 (18)
(18)
 (19)
(19)
其中, ,
, 。
。
尾桨的反扭力矩为 。
。
3) 机身受力情况:由机身所产生的力可以表示如下
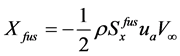
 (20)
(20)
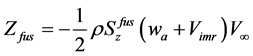
其中 、
、 和
和 分别表示机体的前向、侧向和垂直方向的受力面积,
分别表示机体的前向、侧向和垂直方向的受力面积, 、
、 和
和 分别表示相对于空气机身中心的速度的三个分量,
分别表示相对于空气机身中心的速度的三个分量, ,
, ,
, ,
, ,
, 和
和 表示的风速在坐标轴下的三个分量 [11] 。
表示的风速在坐标轴下的三个分量 [11] 。
4) 垂尾受力情况:垂尾产生的侧向力可表示如下
 (21)
(21)
其中 表示垂尾的面积,
表示垂尾的面积, 表示垂尾升力曲线斜率,
表示垂尾升力曲线斜率, 是尾桨轮毂的轴向速度,
是尾桨轮毂的轴向速度, 表示的是垂尾相对于空气的侧向速度,
表示的是垂尾相对于空气的侧向速度, 是垂向速度。
是垂向速度。
5) 平尾受力情况:平尾产生的Z方向上的力计算公式如下
 (22)
(22)
其中, 是水平稳定杆的面积,
是水平稳定杆的面积, 是升力曲线斜率。
是升力曲线斜率。
2.2. 力矩分析
根据上一章所介绍的受力情况,模型直升机的力矩也包括主旋翼、尾桨、垂尾和平尾的力矩,同时还有转子的扭矩,即 ,分析如下:
,分析如下:
已知主旋翼的受力情况和桨毂中心距直升机重心高度 ,可得到主旋翼的力矩在坐标轴下的三个分量为 [12]
,可得到主旋翼的力矩在坐标轴下的三个分量为 [12]
 (23)
(23)
已知尾桨的受力情况和尾桨桨毂中心相对于机体重心的垂向距 和纵向距离
和纵向距离 ,可得到尾桨所产生的力矩为
,可得到尾桨所产生的力矩为
 (24)
(24)
垂尾产生的力矩有滚转力矩和偏航力矩,计算公式如下:
 (25)
(25)
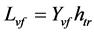
最后,计算平尾产生的俯仰力矩为
 (26)
(26)
 是电机产生的扭矩,
是电机产生的扭矩, ,
, ,
, 是电机功率,
是电机功率, 是电机的最大功率,
是电机的最大功率, 为油门开度控制量,
为油门开度控制量, 。
。
2.3. 转子动力学方程
在模型直升机中,主旋翼总距和油门使用的是联动控制方法,转子的动力学方程可描述为 [13] [14] :
 (27)
(27)
其中, 是主旋翼转速,
是主旋翼转速, 是主旋翼的转动惯量,
是主旋翼的转动惯量, 、
、 、
、 的值在上面已求出。
的值在上面已求出。
3. 闭环控制方法实现
为了实现系统的闭环控制,首先就要设计模型直升机的数学模型结构图,整个系统的控制过程为由主旋翼、尾桨、垂尾、平尾、机身和转子组成的数学模型产生力与力矩,然后受力方程产生力提供给平移方程,力矩方程产生力矩提供给转动方程,最后根据平移方程得出的 和转动方程得出的
和转动方程得出的 经过动力学模型可得到模型直升机的状态量,其设计框图如图2。
经过动力学模型可得到模型直升机的状态量,其设计框图如图2。
然后加入闭环控制环节,并在其中引入PID控制器,既能加快系统的响应速度,又能消除误差,提高稳定性,结合模型直升机的模型,本系统中控制器设计的基本思想如图3。
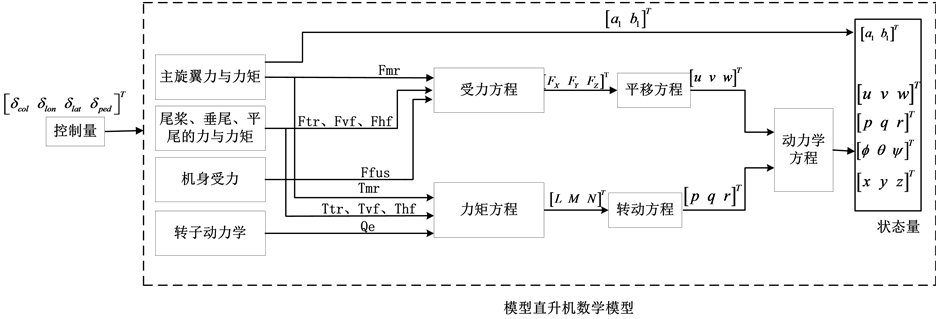
Figure 2. Mathematical model of model helicopter
图2. 模型直升机数学模型
其中,r(k)表示输入量,在本系统中为 ,y(k)表示系统输出的返回值,为
,y(k)表示系统输出的返回值,为 ,e(k)表示系统的误差,即
,e(k)表示系统的误差,即 ,x(k)表示系统的状态量,为
,x(k)表示系统的状态量,为 、
、 、
、 、
、 ,K1和K2是通过极点配置得到的系数矩阵,u(k)表示系统的4个控制量,为
,K1和K2是通过极点配置得到的系数矩阵,u(k)表示系统的4个控制量,为 ,从而控制整个模型直升机,最后输出模型直升机的状态量作为反馈环节引入到输入部分,影响控制量,从而形成系统的完整闭环结构。
,从而控制整个模型直升机,最后输出模型直升机的状态量作为反馈环节引入到输入部分,影响控制量,从而形成系统的完整闭环结构。
4. 仿真结果
根据上面建立的模型直升机闭环控制结构图,搭建Simulink仿真器,以系统的平衡点为仿真起点,如下图所示,其中 ,
, ,在风速等随机变化的扰动下,可以仿真得到系统状态量的变换曲线。给定系统的相关参数,如表1,不断调节PID的参数,可以得到当P = 100,I = 60,D = 0.1时能够得到很好的仿真结果(图4~图8)。
,在风速等随机变化的扰动下,可以仿真得到系统状态量的变换曲线。给定系统的相关参数,如表1,不断调节PID的参数,可以得到当P = 100,I = 60,D = 0.1时能够得到很好的仿真结果(图4~图8)。
通过仿真结果图可得,在只有给定的x方向的速度的条件下,外加风力扰动,系统能够快速响应并且到达稳定状态,模型直升机可以达到很好的飞行性能。
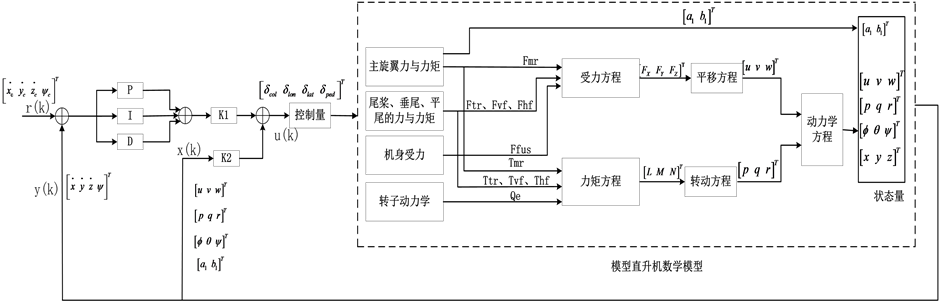
Figure 3. Model helicopter closed-loop control structure diagram
图3. 模型直升机闭环控制结构图
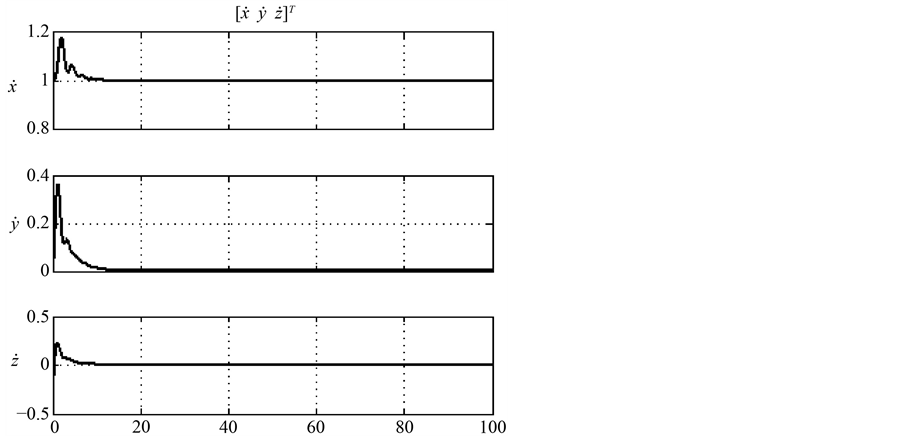
Figure 4. The response line of velocity with time
图4. 速度随时间响应曲线

Table 1. Model helicopter main parameters
表1. 模型直升机主要参数
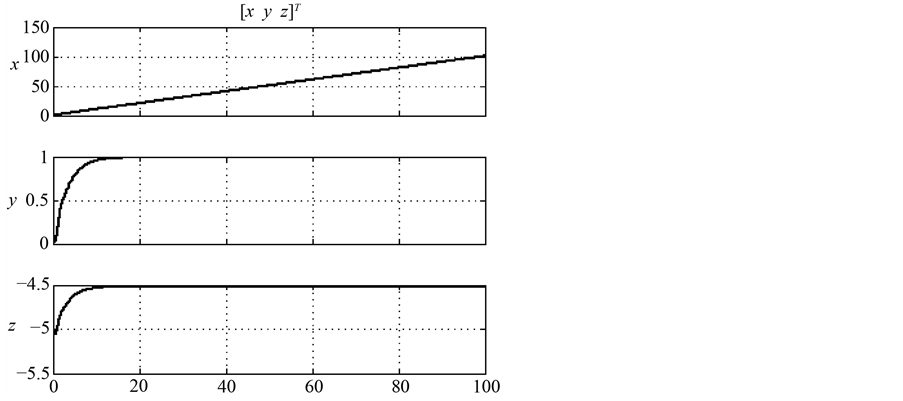
Figure 5. The response line of position coordinate with time
图5. 位置坐标随时间响应曲线
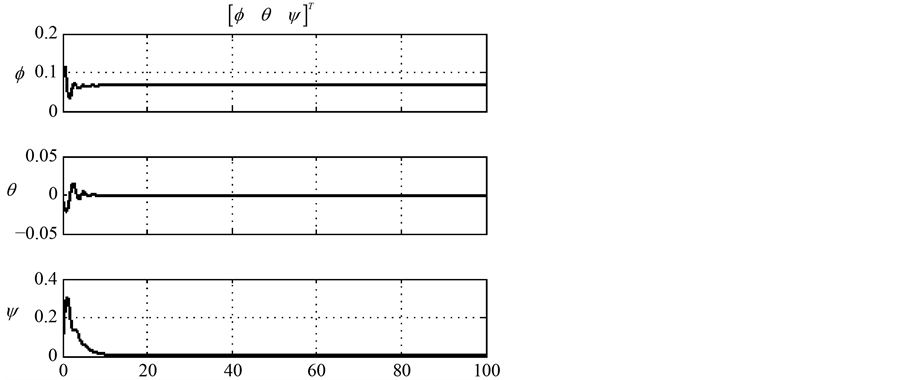
Figure 6. The response line of attitude angle with time
图6. 姿态角随时间响应曲线
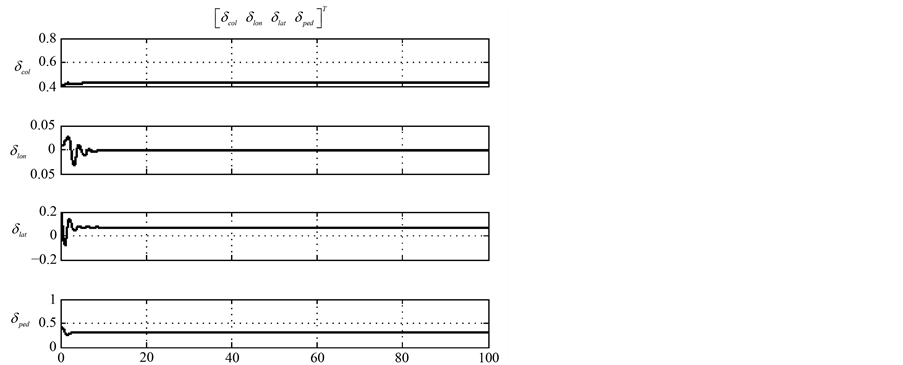
Figure 7. The response line of control variable with time
图7. 控制量随时间响应曲线
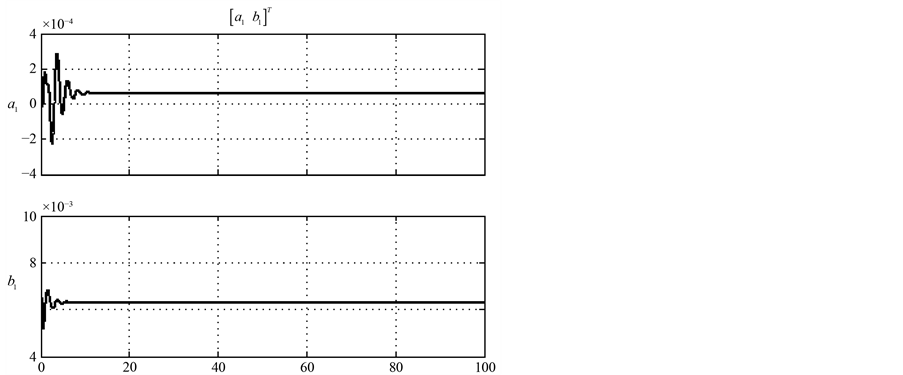
Figure 8. The response line of rotor flapping angle with time
图8. 旋翼挥舞角随时间响应曲线
5. 结论
本文针对模型直升机控制系统,建立了其复杂的非线性方程,考虑转子动力学、旋翼挥舞动力学和机体动力学等,然后用PID闭环控制方法对模型直升机进行建模仿真,消除外界风力的扰动等干扰因素,实现系统的渐进稳定和状态跟踪,仿真结果说明闭环控制方法能够有效的实现系统的控制。