1. 引言
主动式履带铲运机是一种大型的多功能土方机械，主要用于铲土和运土作业，工作环境复杂多变，需要较大的驱动功率，因此广泛采用液压驱动的行走方式。液压传动方式具有功率密度比大、易于调速、安装布置灵活方便等优点。主动式铲运机采用的是双马达的驱动方式，这时两个马达的协调运动尤其是速度同步成为整车能否稳定运行和系统性能指标好坏的关键因素。许多大功率装备驱动系统如大型起重机卷扬系统、包括主动式铲运机在内的重型移动装备行走驱动系统、海洋风电吊装专用船桩腿升降系统等往往尺寸、质量较大，负载扭矩大，故而驱动马达的排量较大，电液控制系统固有频率较低，导致系统的控制精度以及响应速度较低。此外，在大功率装备中，刚性连接往往仅起到防止同步偏差过大，保护执行器和机架的作用，有的甚至没有刚性连接，如重型装备的行走驱动，同步性能完全取决于执行器的同步运动，增加了对于多马达驱动同步性能的要求。
对于多马达同步驱动问题，许多学者进行了大量的研究。刘晓峰等将模糊PID控制算法应用于大型履带起重机双卷扬系统的同步控制，使得系统因非线性和时变性引起的同步误差得到补偿 [1] ，随后又采用单神经元PID控制算法并结合交叉耦合控制方式对该系统的控制性能进一步改善 [2] ；吴宝林等提出一种改进的Narendra MARC方案并用于单泵驱动双马达速度同步系统，取得较好的外负载扰动抑制能力 [3] ；逄波等针对工程机械底盘试验台双马达同步系统提出了基于直接自适应控制和模糊控制相结合的控制方法，改善了系统的同步控制效果 [4] ；李和言等将模糊自适应PID控制应用于高速履带车辆静液传动系统的同步控制，在经受突变载荷干扰时能有效降低了两侧马达转速误差值 [5] ；游张平等针对连续墙液压抓斗起重机双主卷扬同步系统，采用自适应在线遗传PID控制算法取得较好的控制效果，扁担梁水平倾角控制在±0.35˚内 [6] ；魏建华等针对大型装备多轴同步驱动，提出了采用卡尔曼滤波器进行速度估计并结合前馈控制器以及PI反馈控制器提高了系统的响应速度，同步精度在±2 mm内 [7] 。
可以看到，许多学者对于多马达同步系统控制方法进行了大量的研究，并取得良好的控制效果。但是由于大功率马达同步系统基本采用容积调速方式，而容积调速系统固有频率较低，故而单从控制方式上不能从原理上改善其动态性能。为改善大功率马达调速性能，丁海港等提出了阀、泵并联分时变结构调速方案，充分发挥节流调速的快速响应与容积调速的高效率特点 [8] ，但未指出阀、泵同时调节的流量分配。王飞等将阀、泵并联控制的方案应用于海洋风电吊装运输专用船的桩腿同步升降系统，实现了动态特性好的同步控制 [9] ，但是采用阀、泵同控这种统一的、不变的控制结构，没有根据工况来实时合理分配与组合阀控与泵控流量，难以充分发挥阀控快速响应与泵控高效率相结合的优势。
针对以上研究存在的不足，本文以主动式履带铲运机液压驱动行走系统为研究对象，提出了以泵控容积调速为主，旁路并联小流量比例阀进行同步误差补偿的大功率马达速度同步控制系统，建立了旁路补偿系统的数学模型，结合交叉耦合同步控制方式，通过Matlab/Simulink进行仿真并与在相同控制条件下的泵控容积调速同步系统进行对比，验证旁路补偿同步方案的可行性与有效性。
2. 旁路补偿同步方案
旁路补偿同步方案的单通道系统原理图如图1所示，由于在调速过程中只改变单一变量，即只改变比例变量泵排量或是液压马达排量，故而将系统简化为变量泵控制定量马达来研究。比例变量泵与液压马达构成闭式容积调速回路，补油泵用于补充因泄漏而造成的低压侧流量减少，冲洗阀用于加速系统的热交换。旁路比例阀并联在马达进出油路上，通过一个二位换向阀来保证旁路比例阀总是并联于马达的高压进油侧。主调速功能由比例液压泵实现，通过改变比例变量泵的斜盘倾角及倾斜方向可以达到马达速度调节和换向。旁路的小通径比例阀主要用于同步误差补偿，当检测到各个子通道存在同步误差时，通过旁路比例阀对高压侧油液进行补偿。由旁路比例阀的调节造成高低压侧流量不匹配可以通过补油泵和冲洗阀来补偿，当进行高压侧补油时，低压侧多余油液通过冲洗阀或补油泵低压溢流阀回油箱；当进行高压侧泄油时，低压侧不足的油液通过补油泵提供。
下面结合控制方法对旁路补偿方案进一步说明。经典同步控制方法分主从方式与并行方式。主从方式是指将系统中的一个液压马达作为其它马达的跟踪对象，从而实现同步驱动的控制形式；并行方式是指系统中所有马达同时受到相同控制以跟踪理想速度的控制形式。1980年，Koren提出交叉耦合控制方式应用于多电机同步控制，即在对单通道进行控制时，考虑其它控制子通道的状态并进行补偿 [10] 。这种控制方法较为复杂，但同步性能较前两种好，其控制原理如图2所示。
本文结合交叉耦合控制方法与阀泵并联调速系统提出旁路补偿同步控制方案，其控制原理如图3所示。常规容积调速同步系统交叉耦合控制方案中(图2)，各通道的状态差值反馈信号经同步误差补偿控制器后直接作用于比例变量泵的控制器，这样系统的响应速度取决泵马达容积调速系统的频率；而旁路补偿交叉耦合控制方案中，各通道的状态差值反馈信号经同步误差补偿控制器后作用于旁路的比例阀，通过旁路比例阀对高压侧的流量进行调节以补偿同步误差，由于采用阀控补偿，故而调节响应快速。其中，旁路比例阀只对同步误差进行调节而不参与对速度的跟踪控制，故而其额定流量只需满足在极端工况下各通道误差最大值即可，这样对阀控与泵控的流量进行动态的最佳分配，充分发挥了阀控的快速高精度与泵控的高效率。
1 比例变量泵；2 补油泵；3 冲洗阀；4 旁路比例阀；5 二位换向阀；6 液压马达
Figure 1. Diagram of single-channel hydraulic system
图1. 单通道液压系统原理
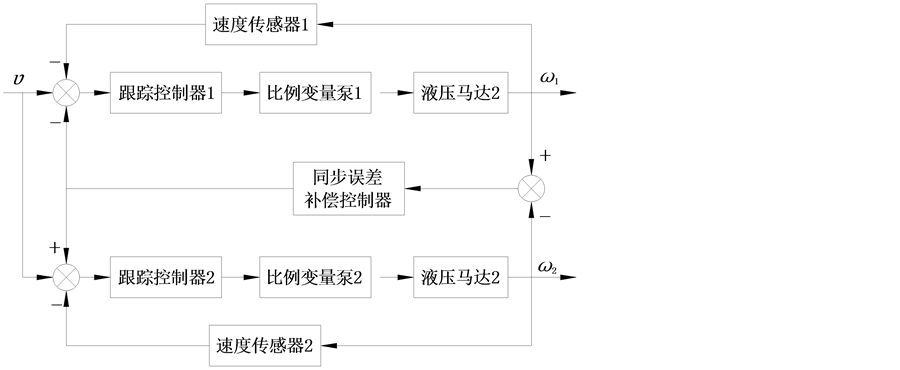
Figure 2. Principle of volume speed-modulating system with cross-coupling control
图2. 容积调速系统交叉耦合控制原理
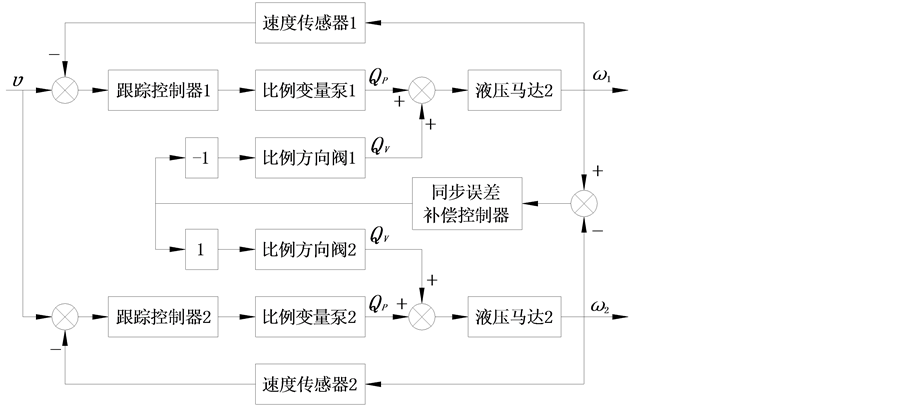
Figure 3. Principle of bypass compensation system with cross-coupling control
图3. 旁路补偿交叉耦合控制原理
3. 旁路补偿数学模型
3.1. 比例变量泵流量
比例变量泵是通过一个比例换向阀控制变量油缸活塞的位移来实现斜盘倾角的改变从而改变液压泵的排量。比例换向阀可以看作二阶环节，其阀芯位移Xc(s)对控制电压U(S)的传递函数为：
(1)
式中，ωc为比例阀固有频率，ξc为比例阀阻尼系数，Kc为控制比例阀增益系数。
零开口比例阀压力-流量线性化方程为：
(2)
式中，kq1为控制阀流量增益，kc1为压力流量系数。
变量油缸前腔输入流量的连续性方程为：
(3)
式中，t为活塞工作面积，xt为活塞位移，kt为活塞间隙的泄漏系数，由于控制压力Pc较小，活塞密封效果较好，可忽略上式第二项。
对变量杠活塞受力分析可得：
(4)
联立上述(2)~(4)式进行拉普拉斯变换可得：
(5)
式中
为变量缸固有频率，
，
为阻尼系数，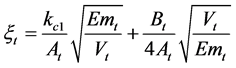
变量泵输出流量为：
(6)
式中np为泵的转速，kp为泵的结构参数。
代入上述5式中可得：
(7)
3.2. 旁路补偿系统数学建模
为了简化模型，在推导系统数学模型时，做几点假设：1) 不计入管道的压力损失；2) 泵的转速为定值；3) 液流密度、温度油液体积弹性模量均为定值；4) 旁路比例阀进油压力为一定值。
旁路比例阀同样为二阶环节，阀芯位移Xv(s)对控制电压Uv(s)的传递函数为：
(8)
式中，ωv为比例阀固有频率，ξv为比例阀阻尼系数，Kv为比例阀增益系数。
旁路比例阀线性化流量方程为：
(9)
系统高压侧流量连续性方程为：
(10)
式中Ct为泵和马达的总泄漏系数，V0为高压侧容积，Dm为马达排量，ωm为马达输出转速。
忽略摩擦和油液质量，马达与负载刚性连接，根据牛顿第二定律可得马达和负载的力矩平衡方程：
(11)
式中Jm为马达和负载等效惯量之和，Bm为马达粘性阻尼系数，TL为负载扭矩。
联立上述8~10式经拉斯变化可得：
(12)
式中
为系统固有频率，
，
为系统阻尼系数，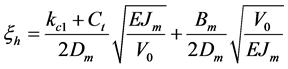
由上述7、8、12式可以得到旁路补偿系统的数学模型，泵控马达数学模型相对而言减少了旁路阀流量这一项，即式10的左边第二项，此处不再推导。
4. 仿真分析
4.1. 仿真模型的建立
为验证系统的性能，在Simulink中建立旁路补偿系统仿真模型，主要仿真参数包括：
；
；
；
；
；
；
；
；
；
；
；
；
；
；
。旁路阀补泵控系统数学子模型如图4所示。子系统包括三个输入信号：变量泵、比例阀的控制信号以及负载扭矩，以及四个输出信号：马达转速1、系统压力2、变量泵输出流量3、比例阀输出流量4。
为验证该方案的效果，本文与同等条件下的泵控容积调速进行了仿真对比，即泵调速同步方案也采用交叉耦合的控制方式，控制原理如图2所示。
系统中每个子通道采用PID控制器对速度进行跟踪，同时采用一个PID控制器对各子通道反馈的信号进行误差补偿控制。按照图3建立旁路补偿系统总的仿真模型如图5所示，同样该方案采用PID进行控制，两方案都采用Z-N方法对控制参数进行整定。
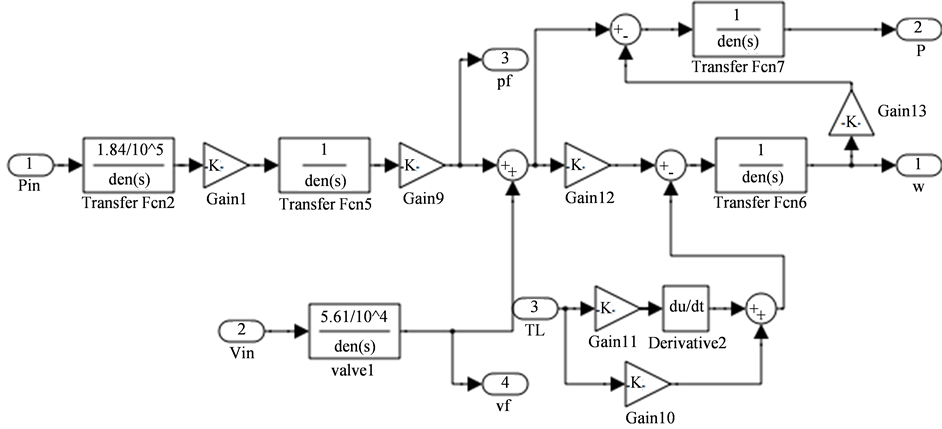
Figure 4. Sub-model of pump control system with bypass compensation
图4. 旁路补偿泵控系统子模型
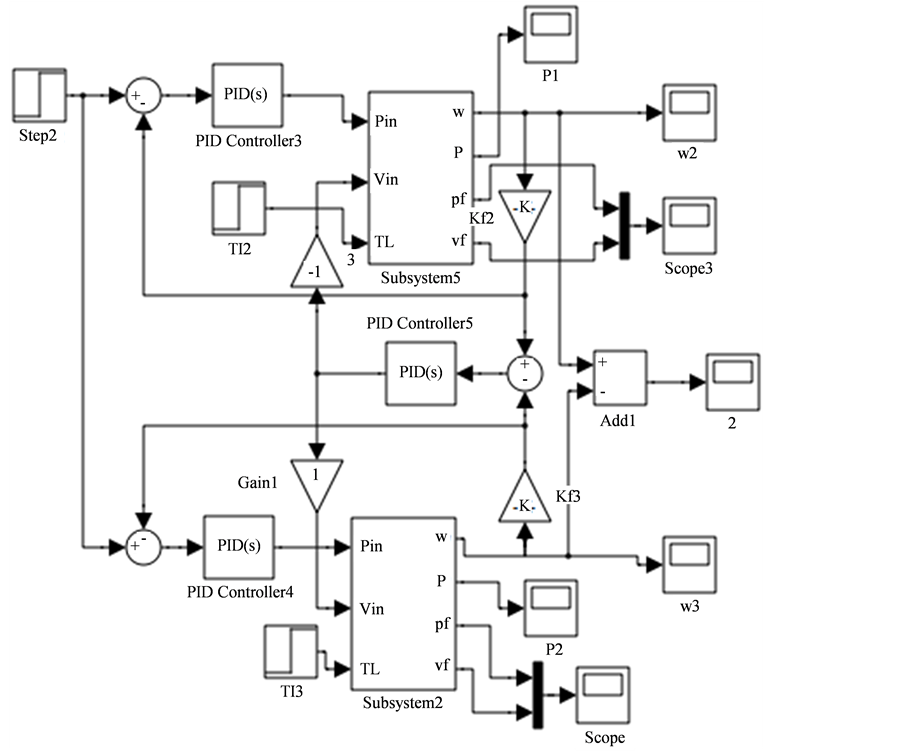
Figure 5. Simulation model of the system
图5. 系统仿真模型
4.2. 仿真结果分析
4.2.1. 稳定偏载下的同步性能
取马达转速阶跃值ω = 1923 r/min，马达偏载扭矩为ΔTL = 600 N/m，两种方案的速度误差曲线如图6所示，其中曲线1为常规容积调速控制方案同步误差，曲线2为旁路补偿交叉耦合控制方案同步误差。
由图6可知，采用常规的容积调速同步控制方案的最大马达转速差值为25 r/min，约占马达转速的1.3%，在1.5 s后误差趋向为0；而采用旁路误差补偿的交叉耦合控制方案马达转速差值为12 r/min，约占马达转速的0.6%，在0.6 s后误差趋向为0。由于采用小通径的比例阀对同步误差进行补偿，因而采用旁路补偿方案在偏载下的误差幅值减小，同步精度更高，调节速度加快。
旁路补偿系统中流量输出可以看到，在稳定偏载下，比例阀调节流量为5.1 L/min，变量泵输出流量在大负载侧为314 L/min，小负载侧为313 L/min。所以马达同步运动所需流量主要由变量泵提供，而同步误差主要由旁路比例阀进行补偿。
4.2.2. 动态偏载下的同步性能
为考虑系统在动态偏载下的同步性能，2.5 s时在其中一侧施加一时长为3 s，幅值为300 N/m的矩形扭矩负载扰动，如图7所示。仿真得到两马达转速差值如图8所示，其中曲线1为常规容积调速控制方案同步误差，曲线2为旁路补偿交叉耦合控制方式同步误差。由图8知，在矩形负载扰动下常规方案马达转速差值为21 r/min，约占马达转速的1.1%，调整时间为1.5 s，后期有小幅振荡；而采用旁路补偿方案马达转速差值为11 r/min，调整时间为0.7 s，抗负载扰动能力强，约占马达转速的0.57%，调节更为快速稳定。
在动态偏载矩形负载扰动下，利用节流调速快速响应的优点对两侧进行流量补偿，即两侧比例阀输出相应的流量用以补偿负载带来的误差，从而实现阀、泵并联控制流量分配的自动调整，系统同步精度更好，响应更加快速，较好的结合了节流调速与容积调速各自的优点。
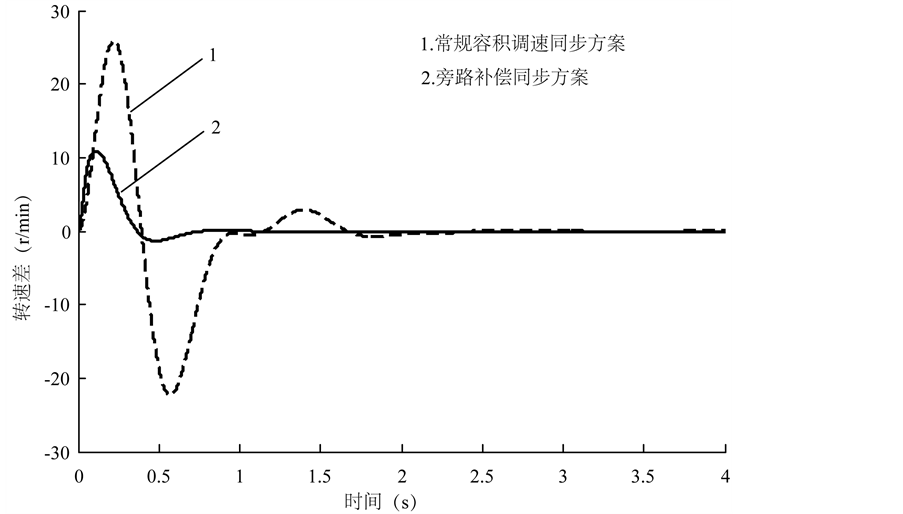
Figure 6. Synchronization error under partial load
图6. 稳定偏载下的同步误差
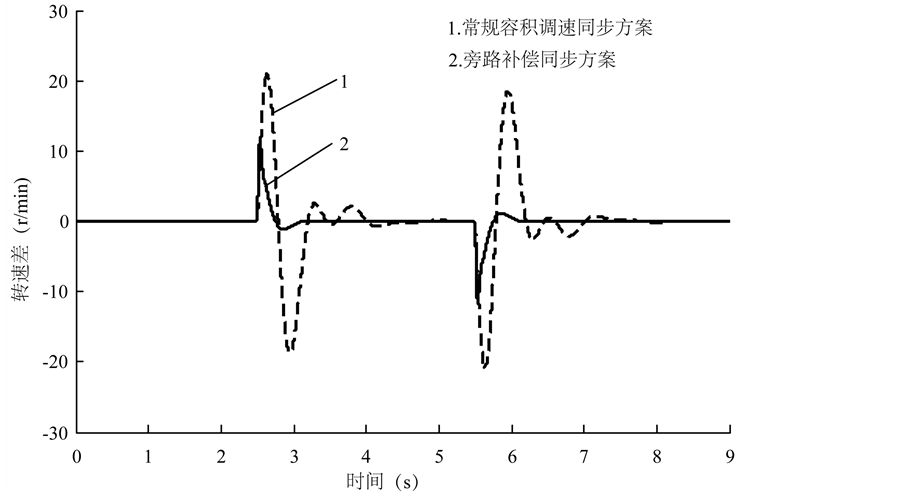
Figure 8. Synchronization error under dynamic partial load
图8. 动态偏载下的同步误差
5. 结论
通过建立旁路补偿的系统数学模型，在Simulink环境中进行仿真并对比相同控制条件下的容积调速同步控制方案，可以得到以下结论：1) 在相同的稳定偏载扭矩以及动态负载下，旁路补偿同步系统的同步误差大幅减少，控制在0.6%内，调节时间缩短了1/2左右，调整过程平稳；2) 马达同步运动所需流量主要由变量泵提供，利用旁路比例阀对容积调速的同步误差进行补偿，较好的结合了节流调速和容积调速各自的优点，达到同步精度高、响应速度快、节能高效的目的。