1. 引言
随着经济的快速发展和人们生活水平的提高,人们对环境和节能关注度越来越高。当前各电厂的发电装机容量都是按照最大需求建设,随着电网峰谷差异日趋增大,必然导致非用电高峰时发电机组的停机或低负荷运行及电网容量浪费。储能可大幅度提高火电机组实际运行效率,增强电网的输电能力。此外,在可再生能源利用方面,风能太阳能等可再生能源具有间歇性和波动性特点,对电网的冲击性很大,导致风能和太阳能发电机组未能并网的比例比较高,这部分的电能浪费比较严重 [1] - [3] 。储能可以实现可再生能源平滑波动、跟踪调度输出、调峰调频等优点,使可再生能源发电稳定输出,从而满足可再生能源电力的大规模并网的要求。压缩空气储能系统利用低谷电,将空气压缩并储存于储气室中,使电能转化为空气的内能储存起来。在用电高峰期,空气从储气室释放进入燃烧室同燃料一起燃烧,然后驱动透平发电。分级压缩过程中空气的温度会随之升高,这部分热量往往被浪费掉。高温空气–熔盐高效换热系统能把压缩空气产生的热量储存在熔盐中。
在生活中还有许多高温空气浪费的地方,主要是由于空气与一些常规蓄热介质之间的换热效率低,加上常规蓄热材料蓄热效果也不佳。熔融盐作为蓄热材料能够很好的解决蓄热效果不佳等问题。熔融盐作为高温传热蓄热材料,具有工作温度高,使用温度范围广、传热能力强、系统压力小、有较高的显热蓄热能力、经济性较好等优点。熔融盐已经作为传热蓄热工质的首选,但是国内外对于强化熔融盐与高温空气传热的研究较少。其主要原因是由于熔盐具有高温、高熔点和腐蚀性等特点,进行熔盐对流传热实验研究难度很大。美国橡树岭国家实验室的H. W. Hoffman [4] [5] 对电加热情况下的NaOH、Flinak (NaF、LiF、KF混合物)、三元熔盐Hitec在圆管内对流换热情况进行了研究,并认为混合熔盐在换热设备中用作传热流体时,可用McAdams,Dittus,和Boelter以及Colburn提出的标准关联式进行设计。在强化熔盐传热方面有在20世纪80年代,Allman [6] 等采用了异型管用于熔盐换热的蒸汽发生器,在Myrosla等人采用内插管增强熔盐侧的换热,以减少太阳能热发电中的吸收器。西安交通大学核科学与技术系 [7] 对核反应器内熔融盐的自然对流进行了数值模拟研究。沈向阳 [8] 等对高温熔盐在螺旋槽管内流动与换热进行了数值模拟,揭示了高温熔盐在螺旋槽管内强化传热的机理,并进一步对阻力性能进行了研究。刘斌 [9] 等学者对熔融盐管内流动进行研究,得出了熔盐管内湍流和过渡流对流换热系数试验关联式,并与已有传热关联式进行充分对比。熔盐与高温空气换热属于气液换热范畴,常规强化换热所采用的换热器为翅片式换热器。对于管内走水或者冷却剂的翅片式换热器的研究前人已经做了大量工作。何明勋 [10] 等对水–空气翅片管换热器进行了实验研究和数值模拟分析,结果发现翅片间距和管排密集度对翅片管换热器性能影响很大,减小翅片间距和增大管排密集度均能增强换热器的换热效果,但压力损失也明显增加。韩建荒 [11] 等对翅片管式换热器传热和流场流动进行了数值模拟,得到其内部流场和温度场的分布规律。但是对于高温空气–熔融盐在翅片换热器中的研究几乎没有。本文对于翅片管式高温空气–熔盐换热器进行数值模拟。
本文以平片形翅片管式换热器为研究对象,应用FLUENT软件对高温空气–熔盐在平片形翅片管式换热器中的换热进行3D的数值模拟。
2. 物理问题及数学描述
2.1. 换热器的基本结构参数及整体模型简化
由于翅片管式换热器整体模型较大,若进行全尺寸的数值模拟,网格划分数量会很多,在实际进行数值模拟计算过程中受到计算机软硬件及其他方面条件的限制,无法模拟出翅片管式换热器整体模型的计算结果。翅片管式换热器的翅片在几何结构方面存在着对称性及周期性,因此可以对翅片管式换热器的翅片平面进行截取,截取出部分单元进行数值模拟 [12] 。本文以方形翅片为研究对象,结构如图1所示,计算区域选为换热通道的一个翅片周期,翅片单位结构尺寸如图2所示,管子内直径DN = 8 mm,管子外直径De = 10 mm,翅片间距S = 2.6 mm,翅片厚度δ = 0.2 mm,翅片长度为22 × 25 mm。为保证计算过程中出口截面处没有回流,出口处有一长通道(通常取5~7倍的管外径),为保证空气入口处流动状态为紊流,入口处亦设有一通道(通常取3~4倍的管外径)。本文取入口为4倍管外径长度,出口为6倍管外径长度。本文所研究的换热器的传热和流动为三维、稳态换热,计算热介质为空气,冷介质为熔盐,物性为常数,采用316L不锈钢管和铝翅片,具体物性参数见表1。
2.2. 模型的网格划分
在翅片厚度层划分1个单元:假设翅片厚度足够薄,翅片壁面温度很快就能达到均匀,翅片内温度沿厚度方向变化很小,可近似认为是一维温度场,计算过程中可以认为在翅片厚度方向上温度相近而不存在温度梯度分布,因此可以不考虑在翅片厚度方向上所产生的变化过程。用Gambit生成计算网格,整个计算区域较难使用单一结构化网格进行划分,需把物理模型划分为三部分:入口段、翅片计算区域、出口段。入口段和出口段釆用以Elements为Tet/Hybrid、Type为TGrid、Intervalsize为1的方式进行划分;翅片计算区域釆用Elements为Tet/Hybrid、Type为TGrid、Intervalsize为0.2的方式进行划分。划分结果如图3所示。
2.3. 边界条件的设定
忽略翅片和钢管的接触热阻;熔盐在管内流动,熔盐进口流速Vh = 0.3 m/s,熔盐进口温度T = 505 K;
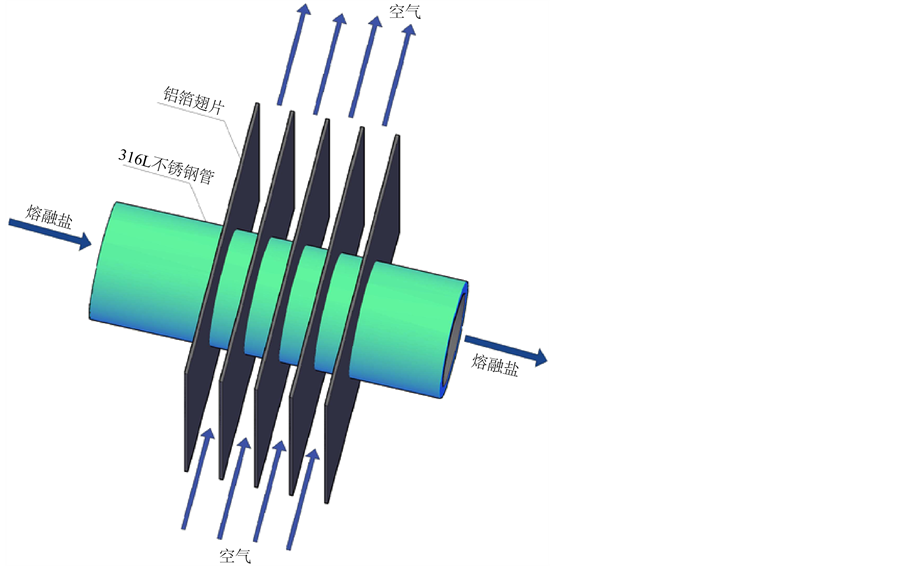
Figure 1. The practical model of finned tube heat exchanger
图1. 翅片管式换热器的实际模型
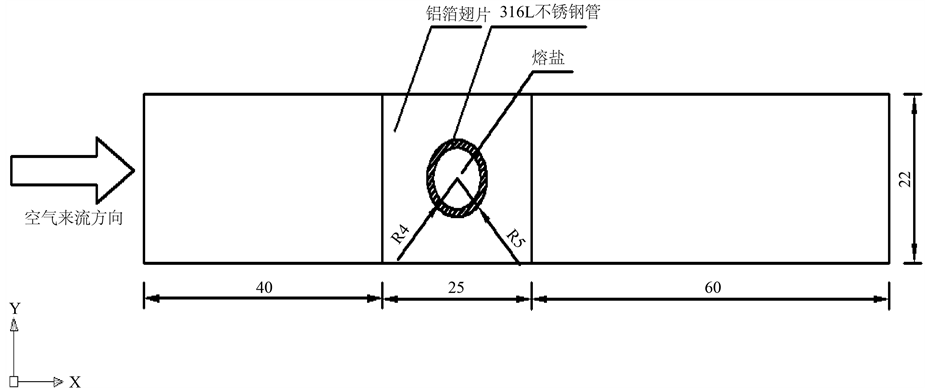
Figure 2. The size of the unit fin (unit: mm)
图2. 单元翅片的尺寸(单位:mm)

Table 1. The physical parameters of high temperature air, molten salt and 316L stainless steel tube
表1. 高温空气、熔盐、316L不锈钢管的物性参数
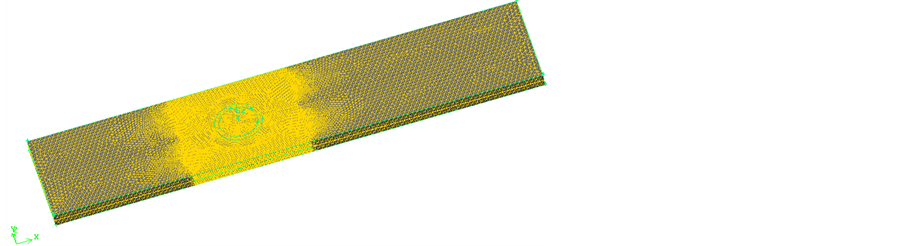
Figure 3. The grid partitioning for the geometric model
图3. 几何模型网格划分示意图
翅片与空气、钢管与空气、钢管与熔盐的接触界面采用流固耦合界面;以翅片为中心的计算区域的边界条件如图4所示,四个侧面为对称边界条件,入口边界采用速度入口,出口边界为压力出口。
2.4. 计算精度及迭代方式的选择
动量方程、连续性方程和其他方程的计算误差均控制为1 × 10−3,能量方程的计算误差控制为1 × 10−6。计算采用FLUENT6.0来完成,连续性方程采用Standard格式,并用SIMPLIEC格式算法处理压力与速度耦合问题,动量方程和能量方程采用二阶迎风格式。
2.5. 控制方程(y,z方向速度为零)
连续性方程:
 (1)
(1)
动量方程:
 (2)
(2)
能量方程:
 (3)
(3)
式中:ρ——密度,kg/m3;
U——速度,m/s;
P——静压,Pa;
T——温度,K;
Α——热扩散率。
3. 数据整理方法
3.1. 当量直径De (按最小过流断面计算)
 (4)
(4)
式中:A——过流断面面积,m2;
P——湿周,m。
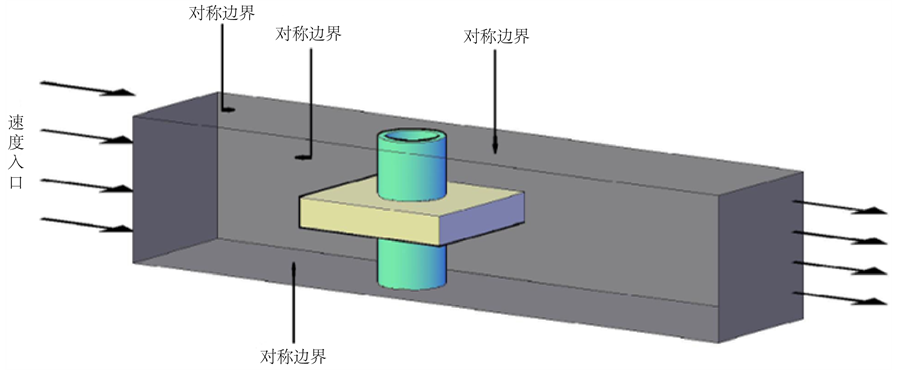
Figure 4. The boundary condition for the calculation area
图4. 计算区域的边界条件示意图
3.2. 雷诺数Re
 (5)
(5)
式中:u——平均速度(直接从FLUENT中读取),m/s;
De——当量直径,m;
 ——运动粘度,m2/s。
——运动粘度,m2/s。
3.3. 公式周期性翅片表面平均阻力系数fm
 (6)
(6)
式中:ρ——密度,kg/m3;
U——平均速度,m/s;
P——静压,Pa。
3.4. 局部换热系数h(x)、平均换热系数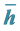
 (7)
(7)
 (8)
(8)
式中:q——热流密度,W/m2;
Twall——壁面温度,K;
Tref——流体参考温度,K;
Tair——空气平均温度,K;
 ——平均温度(下标fin、tube分别表示翅片、基管处的相应参数),K;
——平均温度(下标fin、tube分别表示翅片、基管处的相应参数),K;
A——壁面面积(下标fin、tube分别表示翅片、基管处的相应参数),m2。
4. 数值模拟结果分析
4.1. 速度场分布
图5显示在Re = 500时流体在通道内速度场分布,从图中可以看出流体在通道内速度几乎呈对称分布,在通道的上部和下部,入口到出口流体的流速逐渐增加;绕过管道的两边出现了红色区域,表示该区域速度最大。从图5中我们发现在熔盐管道内部的流体也出现了沿X方向的速度变化,具体情况见图6。主要由于在管子的迎风侧截面受热不均匀,导致管子的迎风侧内部熔盐加热方式属于非均匀加热,熔盐由于受热不均匀形成涡流,从而产生X方向的速度;而管子的背风侧由于空气流动速度几乎为零,没有速度变化,从而受热较均匀,没有产生X方向速度。
4.2. 温度场分布
图7为流体在Re = 500的通道内的温度场变化,从图中看出,温度变化发生在近壁面区域,在迎风侧变化相对明显;由于翅片和管子的存在,流体发生绕流,在绕过管子和翅片的两侧等温线比较密集,在背风侧等温线比较稀疏。图8为空气Re = 500时,Z = 0 mm翅片表面上温度分布,可以看出等温线在翅片迎风侧相对密集,背风侧相对稀疏,这说明迎风侧换热强。
4.3. 空气流速对空气侧表面换热的影响
在翅片结构尺寸一定的情况下,增加空气流速,空气在流动方向上由层流转化为紊流。当空气在Re = 30,000时,在Z = 0 mm翅片平面上的温度分布见图9。由图8和图9比较可以看出,对于流速对翅片表面温度的影响,紊流对翅片的影响比层流均匀,等温线比较均匀,等温线分布也比层流密集,说明紊流的温度梯度大,换热比较强烈,翅片和流体之间的热传递作用也就更加明显,对翅片的换热影响比层流大。
从图10可以看出,随着迎面风速的增大,空气侧表面换热系数逐渐增大,较大的迎面风速能够强化对流换热的效果、显著提高翅片管换热器的传热性能;随着迎面风速的增大,空气侧表面平均阻力系数逐渐减小并趋于平缓。但是风速的增加也具有一定的缺点,由于翅片管换热器自身没有运行动力,需要风机带动空气流动,当迎面风速增加时,相应的风机压力增加,使得风机的能耗大大增加,因此根据经验翅片管式换热器一般的进口空气流速应限制在3~4 m/s范围内。
4.4. 翅片间距对空气侧表面换热系数的影响
从图11分别显示了当翅片厚度为0.2 mm,空气进口速度v = 2.7 m/s时,翅片间距对翅片换热器空气侧换热系数的影响。从图中可以看出适当减小翅片的间距,有利于增加空气侧表面系数。由于翅片间距的减小增强翅片间流体的扰动,使表面传热系数提高;但是减小翅片间距是有限的,一般翅片间距不应小于热边界层厚度的两倍,翅片间距过小,由于翅片表面上的热边界的影响,空气侧表面换热系数将会降低,翅片间距S = 1.3 mm对应的空气侧表面换热系数最佳。
5. 结论
1) 在低雷诺数情况下,由于管子迎风侧受热不均匀,致使管内熔盐形成涡流,从而产生X方向的速度;
2) 翅片结构尺寸一定时,随着迎面风速的增大,空气侧表面换热系数逐渐增大,空气侧表面平均阻力系数逐渐减小并趋于平缓;
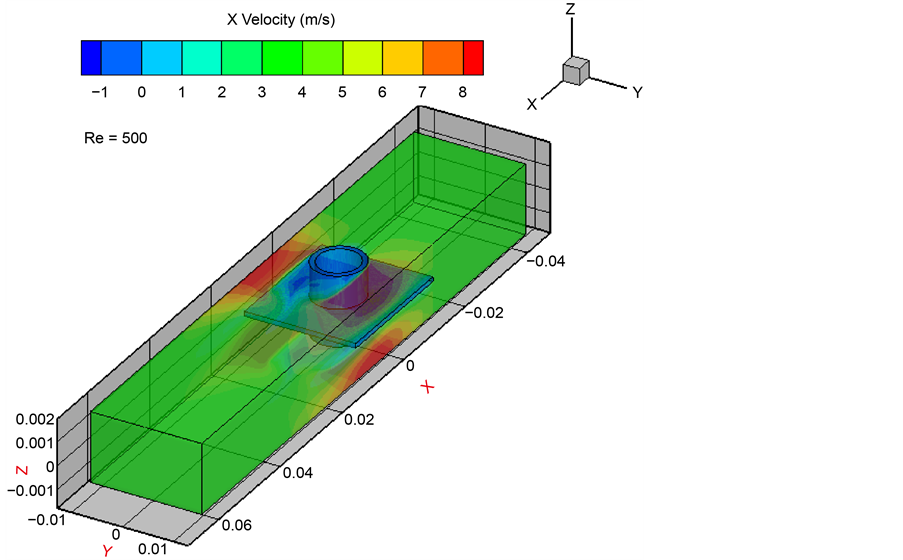
Figure 5. The velocity field of the fluid under the condition of Re = 500
图5. Re = 500时的流体的速度场分布
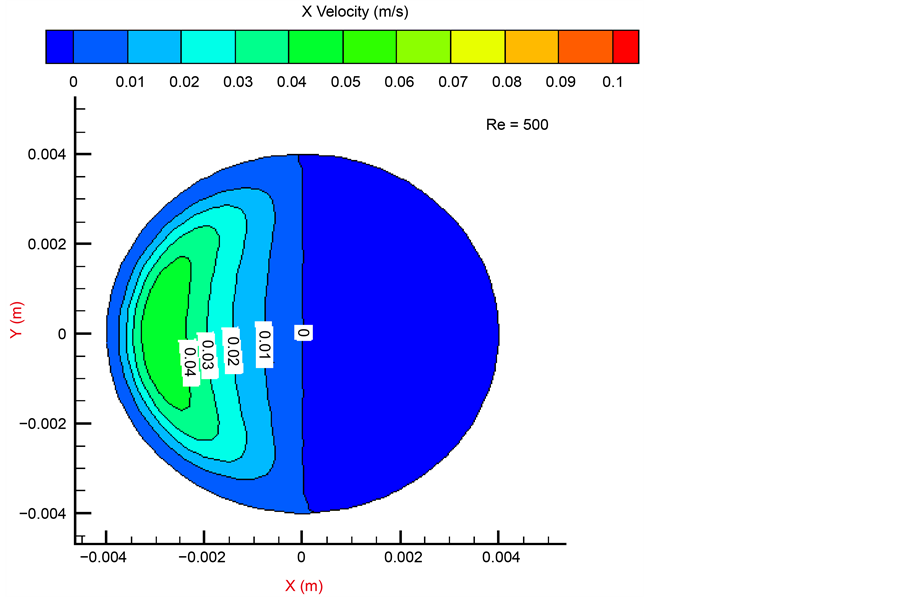
Figure 6. The velocity variation of the fluid inside the tube along the X direction for the Z = 0 mm plane when Re is equal to 500
图6. Re = 500时,Z = 0 mm平面上管内流体沿X方向速度变化
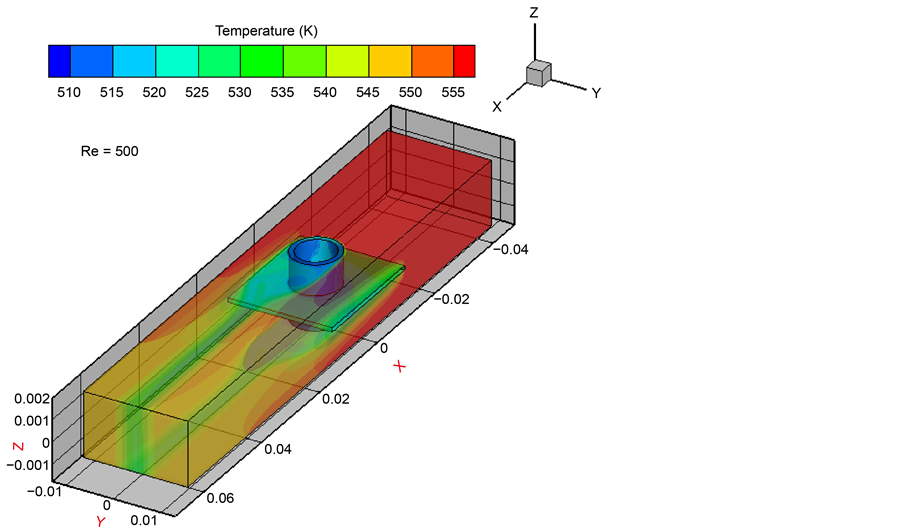
Figure 7. The temperature field of the fluid for Re = 500
图7. Re = 500时的流体的温度场分布
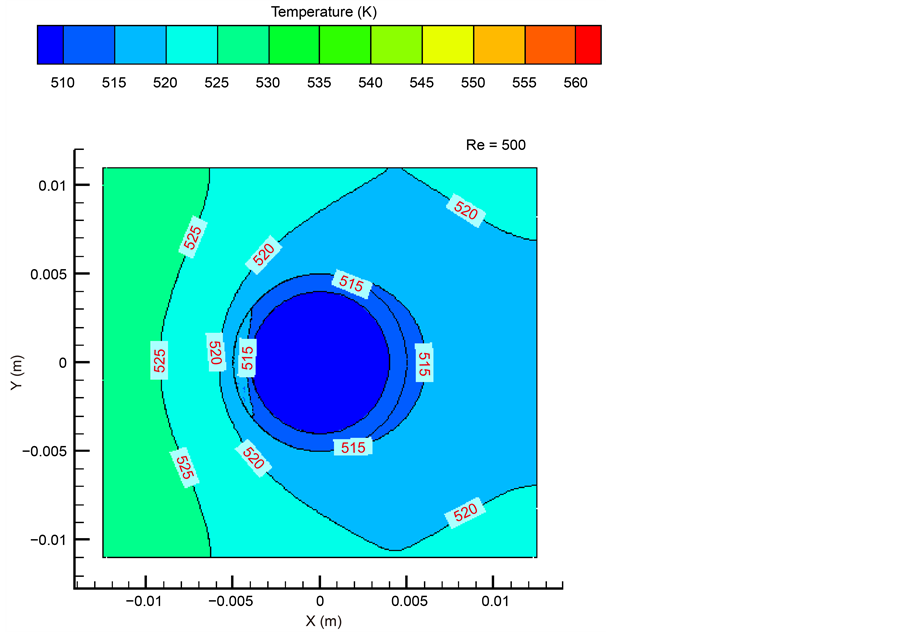
Figure 8. The temperature distribution on the fin surface for Z = 0 mm plane when Re = 500
图8. Re = 500时,Z = 0 mm翅片表面上温度分布
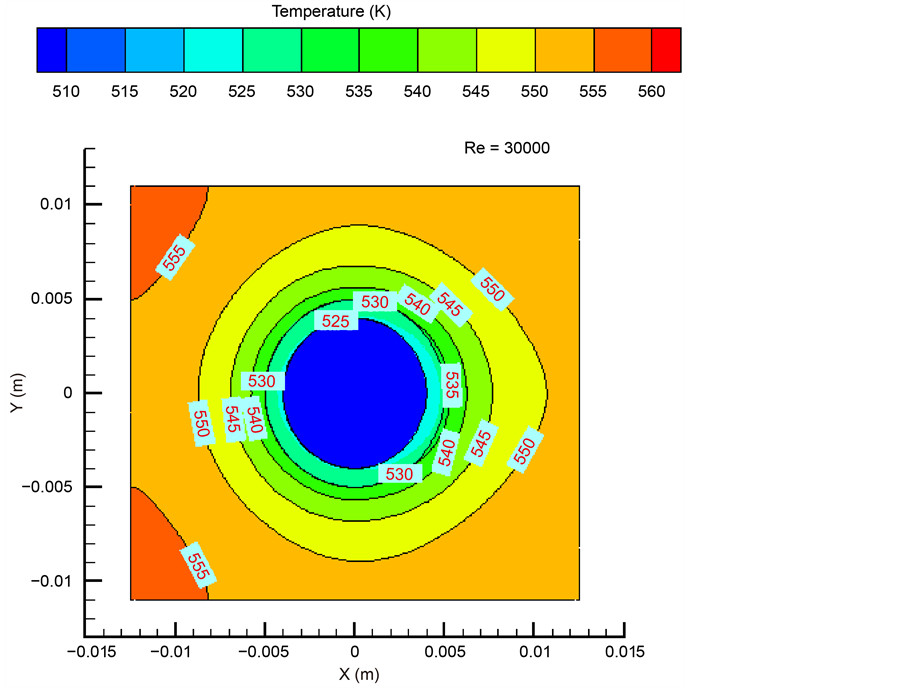
Figure 9. The temperature distribution on the fin surface for Z = 0 mm plane when Re = 30,000
图9. Re = 30,000时,Z = 0 mm翅片表面上温度分布

 (a) (b)
(a) (b)
Figure 10. The effect of velocity for the air on the heat transfer and flow characteristics when the fin space S is adopted as 2.6 mm. (a) The heat transfer coefficient variation of air side with the inlet velocity of air; (b) The average drag coefficient variation with the inlet velocity of air
图10. 翅片间距S = 2.6 mm时,空气流速变化对空气侧换热和流动的影响。(a) 空气侧换热系数随空气进口流速的变化情况;(b) 平均阻力系数随空气进口流速的变化情况

Figure 11. The influence of fin space on the surface heat transfer of the air side
图11. 翅片间距对空气侧表面换热的影响
3) 随着迎面风速的增大,翅片平面上的等温线越来越均匀,温度梯度越来越大,翅片和流体之间的热传递作用也就更加明显,空气侧换热系数逐渐增大;
4) 当空气流速一定时,随着翅片间距的增加,空气侧表面换热系数呈现先增加后降低的趋势,翅片间距存在一个最佳值。当空气进口流速v = 2.7 m/s时,翅片间距S = 1.3 mm对应的空气侧表面换热系数最佳。
基金项目
国家项目:国家“973”项目(No. 2015CB251303),国家自然科学基金(No. 51276005)。
项目名称:中高温储热材料的热物性关联机制与储热单元传热强化机理FAM-Z02型沸石分子筛太阳能吸附空调系统优化应用基础研究。