1. 引言
常见的微型飞行器多采用机械的固定翼或旋翼驱动方式实现飞行,然而自然界中的鸟类、昆虫等都是采用扑翼飞行的方式,具有极高的机动灵活性且消耗很少能量。这种高效的飞行机理是生物几千年来的进化结果,至今仍未能完全解释。因此,借鉴自然界中飞行生物普遍采用的扑翼式飞行方式,将是解决微型飞行器在低雷诺数下飞行难点的一种可行方案 [1] - [3] 。
对于蜻蜓等昆虫飞行时翅膀的运动规律,在此之前已经有很多学者进行了研究 [4] 。德国自动化公司Festo在近几年连续推出了仿生鸟,仿生蜻蜓等微型扑翼飞行器 [5] ,尽管实际尺寸和真实昆虫仍然有一定差距,但已经可以很好的模拟昆虫的运动规律。目前普遍的研究认为,蜻蜓正常飞行时,翅膀具有三个自由度,首先翅膀近似在一个平面上扑动,该平面与水平面有一定的夹角,同时翅膀在扑动平面上扑动的过程中还伴随着自身的异面转动。在此之前的很多研究只是单纯重点分析了蜻蜓飞行时翅膀的运动规律,很少有研究将这种运动与气动特性结合起来。本文首先分析了蜻蜓实际运动规律,推导出了能较好模拟蜻蜓翅膀运动的运动方程 [6] [7] ,其次结合微型机械蜻蜓的设计尺寸,通过计算流体力学软件仿真模拟得到微型机械蜻蜓翅膀在一个扑动周期内的升力变化情况,并分析得到相关结论。
本文采用ANSYS Fluent计算流体力学软件对飞行过程中的机械蜻蜓进行空气动力学仿真,运用动网格技术,编写UDF控制翅翼的运动,最后迭代求解,得到一个扑动周期内空气对蜻蜓翅膀的升力系数并计算升力值并分析总结升力值在一个扑动周期内的变化规律。为了探讨其他因素对蜻蜓飞行时升力的影响,本文还改变其他相关条件,进行多次实验进行横向比较,得到的部分结论将应用到实际微型仿生扑翼飞行器的设计制作上。
2. 实验方案介绍
2.1. 模型设计
机械蜻蜓的翅膀设计简图见图1,为了实现翅膀的三个自由度运动,同时考虑到沿翅根到翅尖各点的线速度及宽度均不相同,利用有限元分析的思想,研究时将蜻蜓翅膀延翼展方向分成多个截面,对每个截面的侧剖面进行气动分析,每个侧剖面上得到的升力系数将用于求得该截面上的升力。最终一个翅膀受到的总升力由所有截面上的升力求和得到。
蜻蜓正常飞行时,翅膀近似在一个倾斜的平面内扑动,同时还伴随着翅膀绕自身翅轴的翼面翻转。建模时,假定蜻蜓延X轴负方向飞行,身体与x轴平行,Y轴为竖直方向,垂直于地表平面。如图2所
示,在该坐标系中可定义翅膀上某个截面的剖面中心的线速度以及该截面绕中心的转动角速度,如此可以在二维平面上实现翅膀的三个自由度运动。
2.2. 网格系统
本试验利用Gambit软件划分非结构网格,所需的边界条件有三类,壁面边界条件,速度入口边界条件,压力出口边界条件。翅膀剖面设为壁面边界条件,满足固定壁无滑移边界条件。位于X轴负方向的边界为速度入口边界条件,另一侧边界则设为压力出口边界条件,求解域的长度为翼宽的20倍左右。
为了尽量减少误差,保证解的精确度和稳定性,网格不仅要能准确反应流体区域的边界形状,较好的适应动网格技术,还要满足网格疏密变化,翅膀剖面边界层附近的网格较密,而远场区域物理梯度较大,网格可以疏一些。本文最终采用的是非结构三角形网格,部分网格划分见图3。
2.3. 数值方法
研究微型扑翼飞行器空气动力学特性的方法主要有三种:理论流体力学方法;风洞实验方法;计算流体力学方法,本文主要采用计算流体力学方法,利用ANSYS Fluent进行数值模拟,基于的控制方程组为纳维斯托克斯方程,同时根据现有条件对方程进行一定的简化。
昆虫拍动的雷诺数较小,蜻蜓正常飞行时的雷诺数只有1000左右 [8] ,因此可以选用层流模型。本文计算工况下空气的流动速度较低,可认为空气是不可压缩,即密度不变的粘性流动,忽略质量力,纳维斯托克斯方程可简化为:
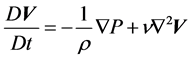
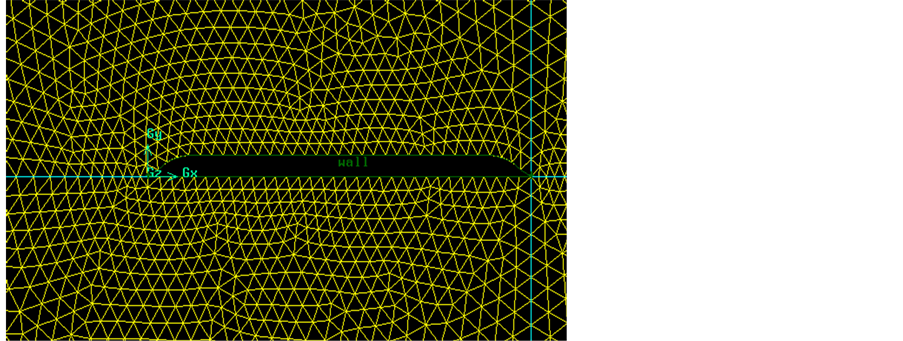
Figure 3. Sectional meshing of wings
图3. 翅膀剖面周边网格划分情况
3. 运动模型
3.1. 运动分析
蜻蜓的扑翼主要由扑动和扭转两种基本形式组成。东京大学的一项研究曾给出了蜻蜓翅膀一个周期内扑动角度随时间变化的离散点(见图4 [9] )。在此基础上,我们考虑到实际微型仿生扑翼飞行器的尺寸和设计,利用正余弦函数对离散点拟合,可以得到如下的运动规律:
水平方向位移: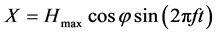
竖直方向位移: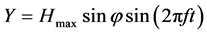
翼面扭转角: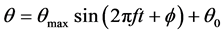
式中 为扑动平面与水平面的夹角,
为扑动平面与水平面的夹角, 为异面转动与扑动平面内平动的相位差,
为异面转动与扑动平面内平动的相位差, 为扑动幅值,
为扑动幅值, 为初始攻角,
为初始攻角, 为最大扭转角,具体取值将根据实际机械蜻蜓的设计尺寸等参数而定。
为最大扭转角,具体取值将根据实际机械蜻蜓的设计尺寸等参数而定。
3.2. 运动实现
本文首先通过编写UDF (用户自定义函数)控制翅膀的运动。主要调用的宏有DEFINE_CG_MOTION,计算求解时以翅膀上某个截剖面为单位,因此在函数中可以定义该计算面在扑动平面上的线速度,以及绕自身重心的转动角速度随时间的变化情况。在ANSYS Fluent中定义动网格模型,本文所用到的动网格再生方法有弹性光顺(Smoothing)、局部重构(Remeshing),编译UDF,导入计算剖面的运动模型,预览一个周期内的网格运动,整体网格质量都保持得较好,没有出现过度挤压或拉伸等情况。
4. 计算结果及分析
4.1. 运动实现
选取本次实验其中的一个工况,将得到的一个周期内升力系数随时间变化曲线与哈尔滨工业大学曾经的一项类似研究结果 [10] 作对比(见图5)。选取工况的截面宽度为1.5 cm,飞行速度5 m/s,扑动频率为8 HZ,幅值2 cm,结果见图6,可以看出,虽然由于设计尺寸不同,本文与文献在具体参数取值上有差别,最终的数值结果不完全相同,但一个周期内曲线的变化趋势基本相似,因此可以验证本文算法的有效性。
在本文最后还将用傅里叶级数拟合从另个角度进行算例验证。
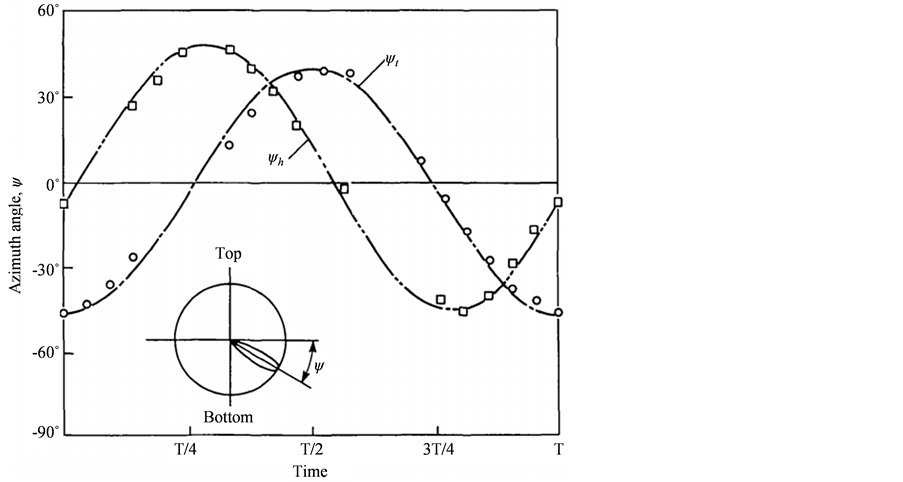
Figure 4. Trace of azimuth angle [9]
图4. 扑动角变化曲线 [9]
4.2. 最大攻角150˚下的升力系数变化情况
根据实际蜻蜓的运动情况,初步选定扑动平面为45˚,飞行速度5 m/s,运动规律和其余计算参数如下:
扑动频率: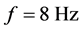
扑动幅值: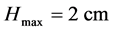
初始攻角:
最大扭转角: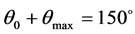
对翅膀中心处宽度为2 cm的截剖面进行计算求解,每3个步长保存一次数据,一个周期内的升力系数和升力值的变化见图7。
从图7中可看出,当攻角大于90度时,升力系数会产生负值,此时翅膀处于后仰状态。理论上分析这种情况是必然的,水平的空气来流对处于这种后仰状态的翅膀有竖直向下的分力,升力系数自然也会出现负值。
4.3. 最大攻角90˚下的升力系数变化情况
由于在设计扑翼飞行器时存在重量等条件限制,为了能较好的拟合蜻蜓翅膀运动规律,同时又能尽可能的创造最大升力,在设计机械蜻蜓翅膀的俯仰运动时,可以避免出现翅膀的后仰状态(即攻角大于90度),这样就可以保证一个扑动周期内的大部分情况,翅膀所受到的升力均为垂直向上的,足够的升力更能保证微型机械蜻蜓的试飞。
在此基础上我们对运动方程进行部分改进,设定最大攻角为90度,即一个周期内攻角都是锐角,其余条件基本不变。本次试验延翼展方向总共选取3个截面,计算截面的宽度分别为2 cm、1.5 cm、1 cm,一个周期内各截面升力系数随时间的变化情况见图8。随着选取截面宽度的降低,升力系数略有下降。
4.4. 飞行速度对升力的影响
取翅膀几何中心处的剖面,在飞行速度分别为2 m/s、5 m/s、10 m/s时作对比试验,得到的升力系数变化曲线见图9。可以看出飞行速度对升力系数的影响非常显著,速度越快,升力系数越大。
4.5. 单个翅膀升力值的变化情况
得到了一个翅膀上每个截面的升力系数,根据升力系数的定义式:
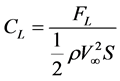
计算得到每个截面上的升力值,将三个截面的升力值相加,得到一个翅膀上总升力值随时间的变化曲线,如图10所示。根据图中得到的最大升力值,假设蜻蜓4对翅膀互不干涉,则飞行产生的升力约相当于7.3 g的重量,足以支撑起一只质量在5 g左右的普通蜻蜓。
由升力值在一个周期内的变化曲线可看出,在从开始运动的0时刻到约0.03秒时刻的这前1/4个周期内,翅膀作下扑动作,升力值由高到低变化,在紧接着的1/2周期内,翅膀作上扑,升力值先升高后降低,最后的1/4个周期内再作一段下扑,升力值继续升高。
将一个周期从开始到结束平均分成4个部分,计算得到每1/4个周期内的平均升力值(见表1)。从表中可看出,在两次下扑过程中产生的升力值明显高于上扑过程中产生的升力值,由此可以得出结论,蜻蜓正常飞行时的翅膀扑动过程中,下扑过程中更有可能产生较大的升力值。
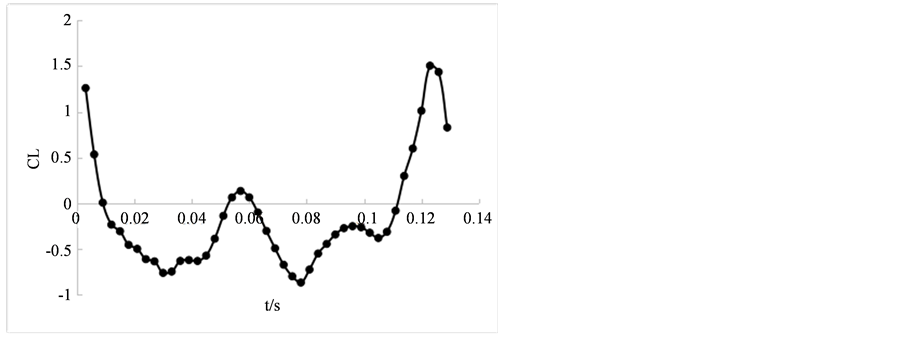
Figure 7. Lift coefficient curve with the maximum angle 150˚
图7. 最大攻角150˚工况下的升力系数变化曲线
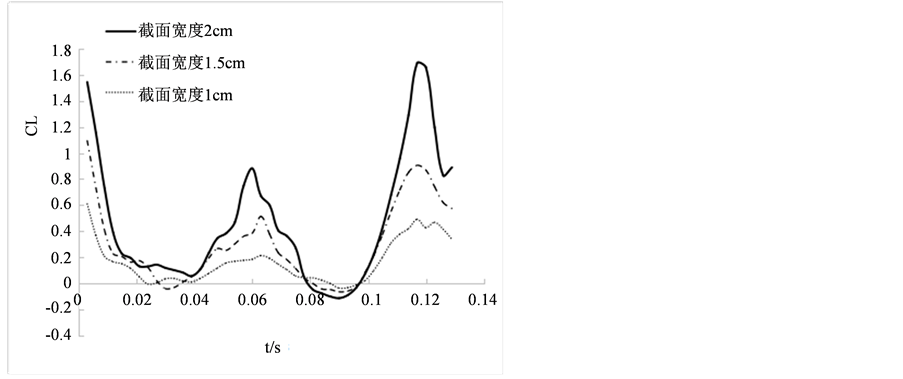
Figure 8. Lift coefficient curve with the maximum angle 90˚
图8. 最大攻角90˚工况下的升力系数变化曲线
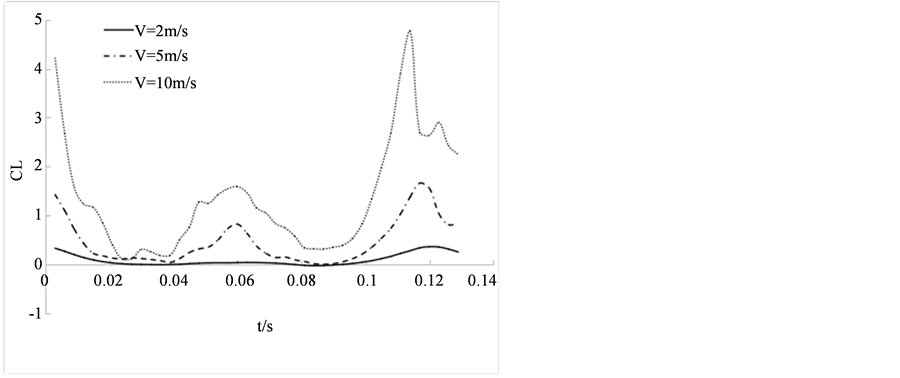
Figure 9. Lift coefficient curve under different flight velocities
图9. 不同飞行速度下升力系数变化曲线

Table 1. The average force in each quarter circle
表1. 每1/4个周期内升力的平均值
4.6. 傅里叶级数拟合结果
本文除了利用正余弦函数拟合蜻蜓翅膀的运动方程,还利用了傅里叶级数拟合来作对比实验,得到的运动方程在拟合程度上比正余弦函数更好,但由于函数书写相对繁琐,仅用来验证本算例结果的有效性。
在蜻蜓的一个扑动周期内取大量的离散点,利用傅里叶级数拟合,得到翅膀前后摆动角度,上下俯仰角度随时间的变化曲线方程:
前后摆动角度: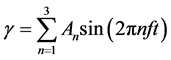
上下俯仰角度: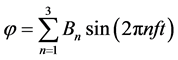
通过对离散点的拟合,得到拟合曲线的具体参数:
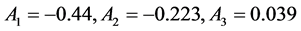
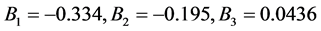
当n > 3以后的值非常小,在此省略不计。模拟求解时其余运动参数都与正余弦函数下的情况相同,由此计算得到三个截面的升力系数随时间变化曲线(见图11)。
可见在傅里叶级数拟合下的各截面升力系数变化曲线与正余弦函数拟合下的曲线非常近似,这也验证了本文计算结果的有效性。
5. 总结
本文分别通过正余弦函数和傅里叶级数拟合蜻蜓翅膀运动规律。根据计算得到的结果和分析可以总结以下结论:
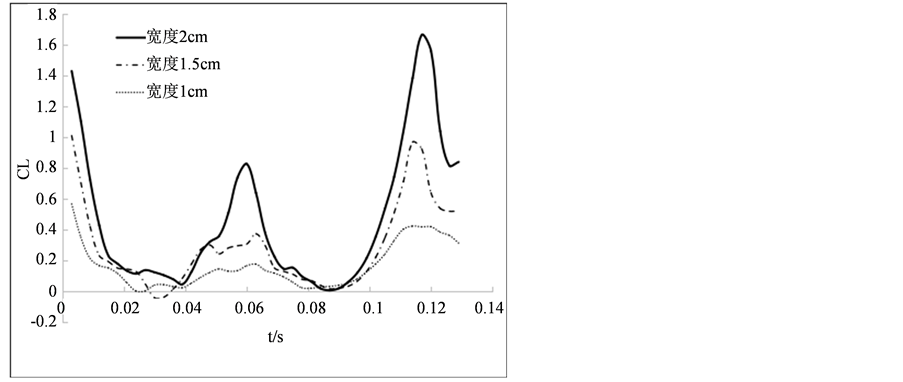
Figure 11. Lift coefficient curve on each wing under the Fourier series fit
图11. 傅里叶级数拟合下各截面升力系数变化曲线
1) 蜻蜓在一个扑动周期内,升力呈现的总体趋势是下降上升再下降上升,升力的最大值可能出现在一个扑动周期的开始或结束时期。
2) 翅膀做下扑动作时,升力系数由高到低变化,上扑动作时则相反。同时翅膀作下扑动作时的升力系数普遍大于作上扑动作时的升力系数。因此在实际的机械蜻蜓设计时,可尽量让一个周期内的下扑时间略大于上扑时间来获得较大的升力值。
3) 翅膀攻角对升力值的影响十分明显,自然界的蜻蜓在飞行过程中会有产生负升力系数的时刻,实际在设计机械蜻蜓运动时可以考虑避免这种情况。
4) 蜻蜓的飞行速度对升力影响非常显著,同时翅膀的设计尺寸对升力值的影响也较大,较宽的翅膀可能会产生更大的升力系数。在机械蜻蜓的制作中,可以根据本文的部分计算结果综合考虑样机重量、尺寸等参数的设计。
基金项目
国家自然科学基金资助项目(51375092)。东南大学基于教师科研的大学生创新实践研究资助计划资助(T16612007)。