制动盘热机耦合分析安全余量方案设计

Schematic Design of Safety Margin during Disc Thermal-Mechanical Coupling Analysis

摘要: 本文提出在制动盘热机耦合分析时考虑安全余量，以200 km/h高速列车为例，设计了4种安全余量仿真方案，分析两次紧急制动工况下制动盘温度场和应力场，结果表明增加减速度方案的计算安全系数最高，增加速度方案的计算安全系数最低，增加轴重方案和降低制动盘许用范围方案居中。

Abstract: An innovative idea of taking consideration of safety margin during disc thermal-mechanical coupling analysis was proposed. One high speed train at 200 km/h as research model was taken for 4 different working conditions about safety margin in simulation. It aimed to analyze simulation results of temperature field and thermal stress field of braking disc after twice urgent braking. The outcomes obtained showed that the calculated safety factor would be the biggest under “de-celeration” condition, while the “acceleration” condition results in the smallest factor. Two other suppositions of “addition of axle load” and “reduction of allowable disc area” are mediate.

1. 引言

高速列车制动装置基本上采用盘形制动，在制动过程中制动盘最高温度和受到的最大应力关乎到制动装置工作的稳定性和列车运行的安全性。通过试验的方法精确获取制动盘瞬时温度和应力分布是比较困难的，目前普遍采用数值模拟的方法来预测制动盘在整个制动过程中的温度场和应力场。尽管有限元仿真方法很成熟，也能在一定程度上很好的反映出制动盘的温度场和应力场大致分布以及变化趋势，但由于在建立仿真模型、施加边界条件过程中存在诸多简化和假设，仿真所得结果与实际情况可能会有些出入。仅仅以仿真结果直接作为制动盘在实际设计和使用过程中的依据，会存在一定的风险。为此，本文提出在制动盘热机耦合仿真分析中适当地考虑安全余量，以200 km/h高速列车为例，针对仿真过程中涉及到的参数，设计了不同的安全余量方案，并将每个方案的仿真分析结果进行对比，分析每种方案不同的适用情况。

2. 方案设计

直接将有限元数值模拟结果作为制动盘实际设计和使用时的依据会存在一定的风险，针对这一问题可以在仿真分析的过程中考虑一定的安全余量。采用热流密度法来模拟制动盘温度需要先计算制动过程中热流密度随时间的变化关系，热流密度公式 [1] 见式(1)。根据热流密度的计算公式，可以分别就车辆轴重、制动时的最高速度，紧急制动减速度以及材料的许用范围考虑设定安全余量。根据列车实际运营环境的复杂程度以及工作人员对安全的重视程度，可对仿真过程中涉及的参数设定不同的安全余量值。本文设计4种仿真方案，以仿真过程涉及到的车辆参数原始值为基础，相应的加重20%作为算例。仿真过程中涉及到的车辆及运行参数原始值见表1，各个方案计算涉及到的变动参数见表2。

(1)

其中：

(2)

为动能转化成热能的效率，参照文献 [2] 。取；为轴重，kg；为制动减速度，m/s²；为制动初速度，m/s；为制动时间，s；为摩擦面数目；为摩擦面积，m²；为热流分配系数；分别为制动盘的密度、导热系数和比热容，分别为闸片的密度、导热系数和比热容。

3. 模型建立

3.1. 有限元建模

本文以200 km/h高速列车制动盘为研究对象，考虑安全余量，分析制动盘在两次紧急制动工况下的温度场和应力场分布情况。在Pro/E中建立制动盘的三维几何模型，考虑到制动盘结构和载荷上的循环对称性，取单侧制动盘九分之一为分析对象。将分割后的几何模型导入到Hypermesh进行网格划分，建立离散的有限元模型如图1所示。该模型包含34,734个节点，162,210个单元。

3.2. 材料参数

本文采用的制动盘材料为25Cr2MoVA，与之配对的闸片材料为粉末冶金。摩擦副材料参数见表3，制动盘的相关性能参数见表4。

3.3. 热流密度

列车制动的过程实际上是动能转化成热能的过程。制动盘与闸片摩擦作用产生热量，随着制动过程的进行，流入制动盘的热量在制动盘内部传导，同时制动盘表面与空气进行对流散热和辐射散热。

根据传热学理论 [3] [4] ，对于无内热源的各向同性材料，其热传导方程为：

(3)

Table 1. Basic values of vehicle and operating parameters

表1. 车辆及运行参数基础值

Table 2. Variable parameters refer to different simulation schemes

表2. 不同仿真方案计算涉及到的变动参数

Figure 1. Simulation analysis model of 1/9 one-side disc

图1. 单侧制动盘九分之一仿真分析模型

Table 3. Material parameters of friction pair

表3. 摩擦副材料参数

Table 4. Reference performance parameters of 25Cr2MoVA disc

表4. 25Cr2MoVA制动盘相关性能参数

其中：T为物体的瞬态温度，℃；为材料密度，kg/m³；c为材料比热容，J/(kg·℃)；为材料导热系数，W/(m·℃)；t为过程进行时间，s。

其初始条件为：

(4)

在制动盘所有的换热界面上

(5)

在参与摩擦的界面上

(6)

其中：为物体的初始温度，℃；为制动盘瞬时温度，℃；为各界面的法向单位向量；为摩擦界面的法向单位向量；为各界面的对流换热系数，W/(m²·℃)；为摩擦界面的对流换热系数，W/(m²·℃)；为各界面的辐射换热系数，W/(m²·℃)；为摩擦界面的辐射换热系数，W/(m²·℃)；为斯蒂芬–波尔兹曼常数，W/(m²·℃⁴)。

相比较对流散热而言，辐射对散热的贡献不大，故而可以仅考虑对流散热对制动盘温度的影响。无内热源的各向同性材料的热传导方程在marc中可转化为如下温度场仿真计算模型 [7] ：

(7)

其中：为比热矩阵；为温度对时间的导数；为传导矩阵；为对流换热系数矩阵；为节点温度向量；为节点热流率向量。

将相应的参数代入热流密度公式计算各个方案热流密度随时间变化的曲线如图2所示。

3.4. 对流换热系数 [8] [9]

制动和加速过程中，制动盘处在强迫对流状态，而内圆周部分可以认为是自然对流换热状态。

气流通过制动盘摩擦面可以采用纵掠平板对流换热模型。气流纵掠平板的雷诺数，根据空气流动状态，盘面的对流换热系数为：

层流，，

(8)

湍流，，

(a)方案一 (b)方案二(c)方案三 (d)方案四

Figure 2. Curve: heat flux varies with time

图2. 热流密度随时间变化曲线

(9)

气流通过制动盘盘缘可以采用横掠单管的模型。气流横掠单管时，，在，时，其对流换热系数为：

(10)

气流通过散热筋可以采用横掠管束的模型。气流横掠管束时，其对流换热系数为：

(11)

其中：为普朗特常数，通过文献 [10] 查得；为空气导热系数，通过文献 [10] 查得； 为空气运动粘度，通过文献 [10] 查得；为空气来流速度，m/s，可近似认为是车速；为制动盘特征尺寸，m；系数可通过文献 [10] 查得。自然对流换热系数取5W/(m²·℃)。根据式(8)~式(10)，代入相应的参数计算可得各个方案制动盘制动过程中的对流换热系数如图3所示。

3.5. 热应力方程

marc求解热应力场时不必再重新建立有限元模型，可以通过软件中的热机耦合模块，将已求解的节

(a)方案一 (b)方案二(c)方案三 (d)方案四

Figure 3. Curve: convective heat transfer coefficient varies with time of different schemes

图3. 不同方案的对流换热系数随时间变化曲线

点温度值作为载荷施加到制动盘结构分析模型上。热应力的计算方程 [11] 为：

(12)

其中：为热应力，MPa；为热膨胀系数，℃⁻¹； 为弹性模量，MPa；为物体的初始温度，℃；为制动盘瞬时温度，℃。

4. 结果分析

车辆及运行参数的改变，热流密度也随之改变。各个参数在热流密度公式中位置不一样，对温度场和应力场仿真结果的影响也就不一样。增加轴重或者降低材料许用范围来考虑安全余量，因不涉及列车运动学参数，故仿真时间与列车运行时间一致。现将四个方案温度最大时刻的温度云图及应力最大时刻的应力云图汇总列于表5中。各个方案中制动盘最高温度节点的温度时间历程曲线和最大应力节点的应力时间历程曲线绘制如图4、图5所示。

从温度和应力随时间变化的曲线来看，方案二的温度最高、热应力最大，方案一次之，方案三再次之，方案四温度和热应力均最小。即速度增加20%模拟出来的工况最苛刻，其次是轴重增加20%，紧急制动减速度增加20%紧随其后。为量化各个方案计算结果的安全程度，引入计算安全系数，其公式为：

(13)

(14)

其中，、分别为温度℃计算安全系数和应力计算安全系数；、分别为制动盘许用温度和计算温度，℃；、分别为制动盘许用应力和计算应力，MPa。不同方案的温度和热应力计算安全系数见表6。

Table 5. Maximum temperature nephogram and maximum thermal stress nephogram of different schemes

表5. 不同方案最高温度及最大热应力云图汇总

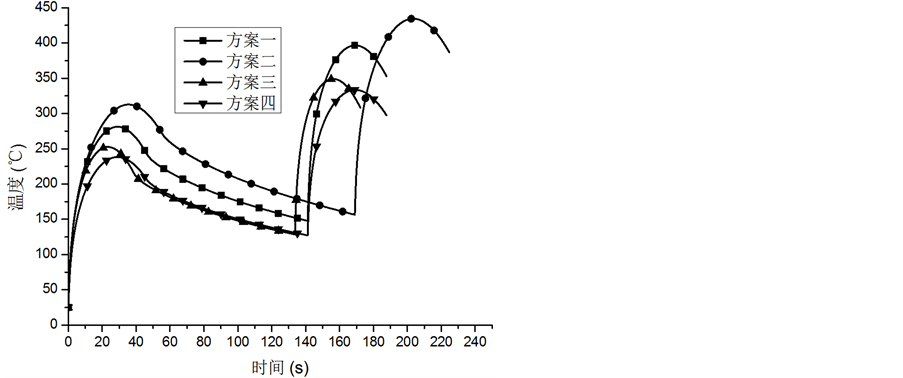
Figure 4. Curve: temperature varies time of maximum temperature node of different schemes

图4. 不同方案最高温度节点的温度时间历程曲线

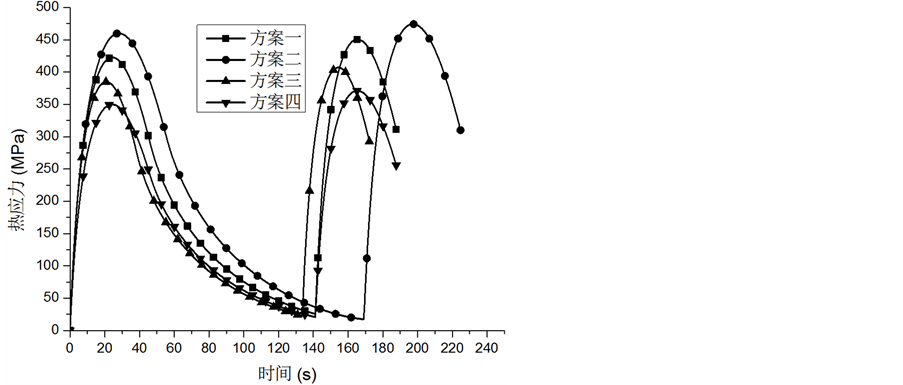
Figure 5. Curve: thermal stress varies time of maximum temperature node of different schemes

图5. 不同方案最大热应力节点的应力时间历程曲线

Table 6. Calculating safety factors of temperature and thermal stress of different schemes

表6. 不同方案的温度和热应力计算安全系数

从计算安全系数来看，方案三的 和 均最大，方案二均最小，即减速度增加20%的方案最为保守，速度增加20%的方案最苛刻，轴重增加20%和许用范围降低20%居中。

5. 结论及建议

(1) 在模拟制动盘温度场和应力场的过程中，对于使用条件比较苛刻的情况可以考虑增加仿真时的最高车速，对于使用条件比较宽松的情况可以考虑增加仿真时的减速度；

(2) 在模拟制动盘温度场和应力场的过程中，增加轴重或者降低材料许用范围来考虑安全余量的方案能够保证仿真时间与实际运行时间一致。

基金项目

“十二五”国家科技支撑计划项目资助(2015BAG13B01-11)；国家自然科学基金项目资助(U1534205)。