1. 引言
Glaisher-Kinkelin常数 被定义为:
被定义为:
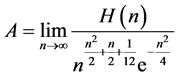 ,(1.1)
,(1.1)
其中,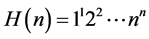 为超阶乘函数。最近,根据Euler-Maclaurin公式,Chen [1] 给出了下列关于超阶乘函数和Glaisher-Kinkelin常数
为超阶乘函数。最近,根据Euler-Maclaurin公式,Chen [1] 给出了下列关于超阶乘函数和Glaisher-Kinkelin常数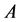 的渐近展开:
的渐近展开:
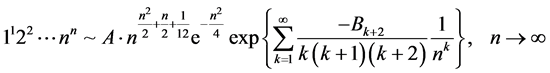 , (1.2)
, (1.2)
其中, 为Bernoulli数。
为Bernoulli数。
在式(1.2)的基础上,Wang and Liu [2] 对超阶乘函数和Glaisher-Kinkelin常数推导出以下一般渐近展开:
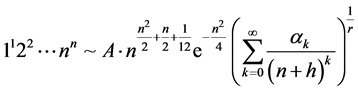 .(1.3)
.(1.3)
最近,我们发现,Chen [1] 还建立了以下关于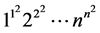 和常数
和常数 的渐近展开:
的渐近展开:
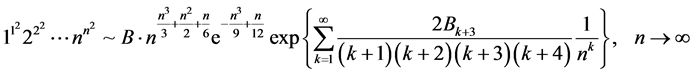 (1.4)
(1.4)
其中, 为Glaisher-Kinkelin常数
为Glaisher-Kinkelin常数 的类似常数。
的类似常数。
以上知识给了我们一个启发,我们希望通过Bernoulli数和指数型完全贝尔多项式去推导出关于Glaisher-Kinkelin常数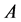 的类似常数
的类似常数 和
和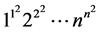 的渐近展开:
的渐近展开:
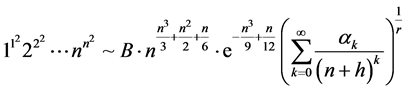 .(1.5)
.(1.5)
为了得到这个渐近展开式,我们需要下列指数型完全Bell多项式的相关知识。指数型完全Bell多项式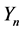 被定义为(见 [3] , Section 3.3):
被定义为(见 [3] , Section 3.3):
 . (1.6)
. (1.6)
它的具体表达式为:
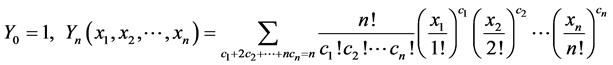 . (1.7)
. (1.7)
另外,根据 [4] , p.36, Equation (44)和 [5] , Theorem 1可以知道多项式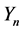 满足递归式:
满足递归式:
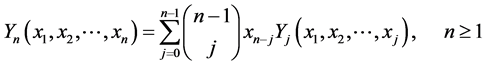 . (1.8)
. (1.8)
2. 定理及证明
2.1. 定理
令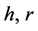 为实数,
为实数,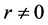 ,并定义
,并定义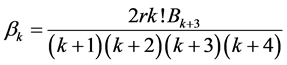 ,则我们有下列关于
,则我们有下列关于 和常数
和常数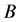 的渐近展开:
的渐近展开:
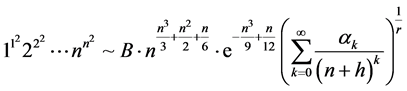 ,
,
其中,当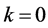 时,
时,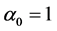 ;当
;当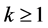 时,
时,
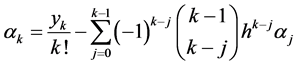 , (2.1)
, (2.1)
在式(2.1.1)中,当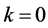 时,
时, ;当
;当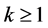 时,
时,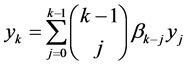 .
.
2.2. 证明
令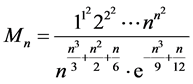 ,由(1.6)以及
,由(1.6)以及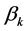 的定义,我们可以将式(1.4)改写为:
的定义,我们可以将式(1.4)改写为:
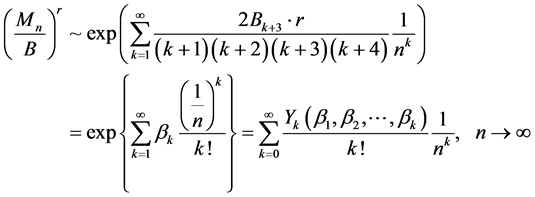
另外,将 展开为关于
展开为关于 的幂级数:
的幂级数:
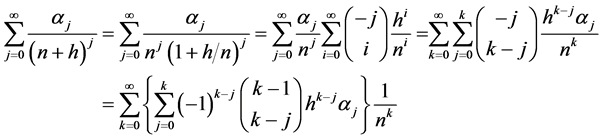 .
.
要证: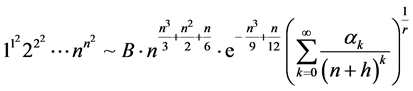 ,即要使下列等式成立:
,即要使下列等式成立:
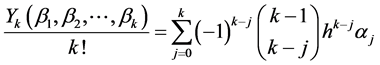 .
.
当我们定义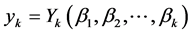 时,上式可以写成:
时,上式可以写成:
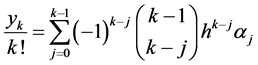 .
.
通过以上等式,我们得到一个唯一解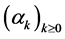 ,而且
,而且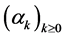 有如下递推关系:
有如下递推关系:
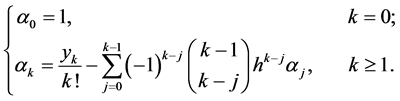
其中, 满足(1.8),定理得证。
满足(1.8),定理得证。
通过指数型完全Bell多项式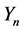 的定义(1.6)我们可以容易地计算出
的定义(1.6)我们可以容易地计算出 。下面我们列出
。下面我们列出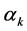 的前几项:
的前几项:
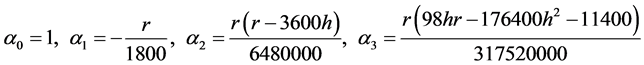 .
.
将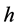 和
和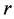 取特殊值,我们可以得到一系列有关Glaisher-Kinkelin常数
取特殊值,我们可以得到一系列有关Glaisher-Kinkelin常数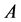 的类似常数
的类似常数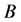 和
和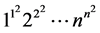 的渐近展开。下面我们举出几个例子。
的渐近展开。下面我们举出几个例子。
3. 例子
令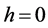 ,
,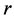 分别取1,2,3,当
分别取1,2,3,当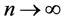 时,我们有:
时,我们有:
 ,
,
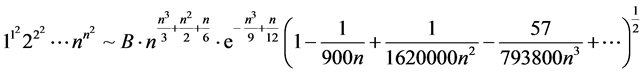 ,
,
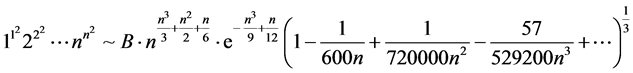 .
.
基金项目
国家自然科学基金/Natural Science Foundation of China (11501081),省级大学生创新创业训练计划项目(项目编号:S201612026050),中央高校基本科研基金(DC201502050405)。
*通讯作者。