1. 引言
本文考虑如下四阶非线性Schrödinger方程的初边值问题
(1.1)
其中
是复值函数，
为常数，
为边界充分光滑的有界区域。问题(1.1)描述的是在Kerr非线性介质中强激光束的稳定孤子的传播模型，其中
为波函数。方程(1.1)有如下守恒律
质量守恒
， (1.2)
能量守恒
. (1.3)
首先回顾经典Schrödinger方程的一些研究结果。Brézis和Gallouët [1] 研究了如下的二阶三次非线性Schrödinger方程
(1.4)
的初边值问题，其中
。该文借助半群理论、能量估计及B-G型不等式
，
且
， (1.5)
建立了解的
范数的先验估计，得到初边值问题(1.4)经典解的整体存在性。事实上，B-G型不等式(1.5)是对经典的Sobolev不等式的改进，即由把线性增长控制减弱为由对数增长控制，这是该文的主要创新点。
Tsutsumi [2] 考虑了更一般的非线性Schrödinger方程
(1.6)
的初边值问题，其中
，对初始条件
加以更多限制，即要求
，
。
作者考虑了
的情形，运用衰减估计、Strichartz不等式及B-G型不等式，得到当
时，
，方程(1.6)存在唯一整体解
，即
，使得
，
和
。
最近，Ozawa和Visciglia [3] 研究了如下半波方程的初值问题
(1.7)
其中
，建立了如下的B-G型不等式
，
， (1.8)
引入能量泛函，运用Yosida正则化准则得到相应的能量估计，进而得到方程(1.7)存在唯一解
，且得到一个新的爆破准则，即
i) 当
时，整体解存在；
ii) 当
，且
时，解爆破。
文 [3] 还研究了如下的二阶四次非线性Schrödinger方程的初边值问题
(1.9)
其中
。作者建立了如下的B-G型不等式
，
， (1.10)
得到方程(1.9)存在唯一解
，且得到一个新的爆破准则，即
i) 当
时，整体解存在；
ii) 当
，且
时，解爆破。
在空间
、
中分别判定问题(1.7)、(1.9)的整体解的存在性，通常是考查其
、
范数的有界性，而该文判定整体解是否存在只需分别考查其
、
范数是否有界即可，这是该文的创新之处。
对于四阶非线性Schrödinger方程情形，Karpman和Shagalov [4] 考虑了如下方程的初值问题
， (1.11)
其中
为参数，且
充分小，
为空间维数。在文 [4] 中分别给出稳定孤子在一维、二维和三维的存在性和稳定性的条件。Zhu，Yang和Zhang [5] 考虑了如下的四阶非线性Schrödinger方程的初值问题
， (1.12)
研究了低正则性解的爆破问题，即考查初值在低正则能量空间
的情形。
上述文献没有给出解的爆破准则。本文希望利用文 [3] 的技巧研究方程(1.1)，借助半群理论及Segel定理，得到初值问题局部解的存在唯一性，并且通过建立一个B-G型不等式，得到初值问题经典解整体存在的一个新爆破准则。
本文主要结论如下：
定理1.1 假设
为边界充分光滑的有界区域，
为常数，并记
，
，
，则对
，方程(1.1)存在唯一经典解
，即
，使得
。
且有如下的二则性原理
i) 当
时，整体解存在；
ii) 当
，且
时，解爆破。
注：一般情况下判定解是否整体存在要考查其
范数是否有界，本文拟对其改进，建立如下的爆破准则。
定理1.2 假设在定理1.1的条件下，存在如下二则性原理
i) 当
时，整体解存在；
ii) 当
，且
时，解爆破。
注：由定理1.2知，判定方程(1.1)的解是否整体存在只需考虑其
范数是否爆破，而在通常情况下判定解是否整体存在要考查其
范数是否有界，这是本文的创新。
本文的安排如下：首先在第一节中介绍背景知识及给出定理1.1和定理1.2；B-G型不等式的构建及
在空间
上具有局部Lipschitz连续的证明将在第二节给出；最后定理1.1及定理1.2的证明在第三节给出，通过引入合适的能量泛函，建立解的
范数估计。
2. 准备工作
类似文献 [3] ，我们首先构建一个B-G型不等式。
引理2.1
具有光滑边界的有界域，对
成立
， (2.1)
证 存在延拓算子P：
，且满足
P是
的有界算子，
P是
的有界算子，
，
，
令
，
记为
的Fourier变换，易知
， (2.2)
， (2.3)
， (2.4)
对
，则有
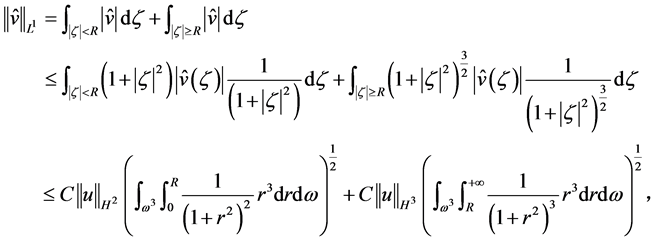
其中
，上式可得
(2.5)
此处用到这个事实：当常数
时，得到
成立，结合(2.4)及(2.5)式，此处取
，因此
。证毕。
引理2.2 记
，
，
，则
具有局部Lipschitz连续。
证 i)易证
，
ii)下证
具有局部Lipschitz连续。
(2.6)
只需对
做如下估计
(2.7)
下面分别对
做估计。
根据Sobolev嵌入定理
， (2.8)
及
，(2.9)
对第一项
进行如下估计
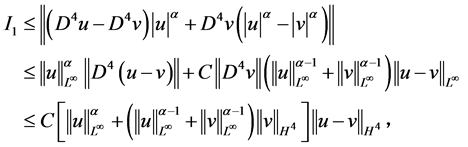
对
做估计
(2.10)
把Sobolev嵌入不等式
， (2.11)
及Gagliardo-Nirenberg不等式
， (2.12)
代入(2.10)得
。
对
进行估计
，
由Sobolev嵌入不等式
， (2.13)
及(2.8)式得
.
对
进行估计
由Gagliardo-Nirenberg不等式
， (2.14)
Poincaré不等
， (2.15)
及(2.8)，(2.13)式得
运用(2.8)，(2.13)及(2.15)式，对最后一项
进行估计
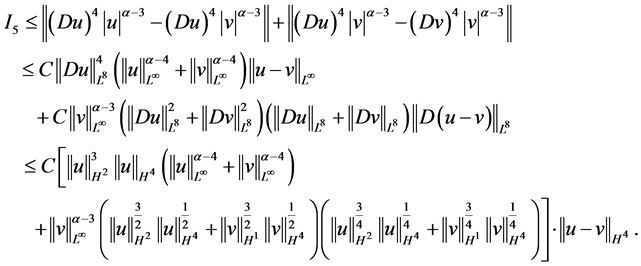
基于
的估计，得
具有局部Lipschitz有界。证毕。
3. 主要结论的证明
下面分别对定理证明。
3.1. 定理1.1的证明
证 由于
为自伴的m-增值算子，又根据引理2.2得
具有局部Lipschitz连续，则由segel定理 [6] ，可得定理1.1成立，证毕。
3.2. 定理1.2的证明
事实上，我们只需证明
有界可推出
有界。
首先引入下列能量泛函
，
引理3.2.1在定理1.1的条件下，则有如下等式
(3.1)
证 由(1.2)式，则有
(3.2)
把(3.2)式中第二项变为
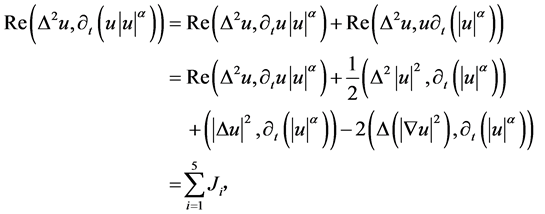
其中
经计算得
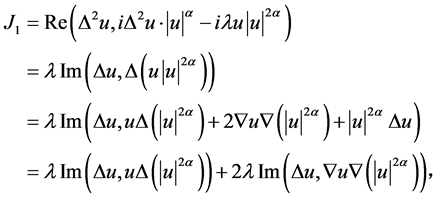
对于
的计算如下
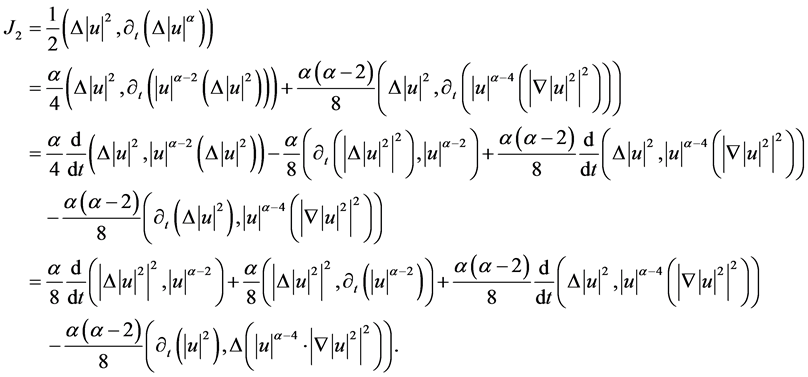
此处
为常数。
引理3.2.2在定理1.1的条件下，且
，得
， (3.3)
证 由引理3.2.1，可知
下面分别给出
的估计，其中第一项估计为
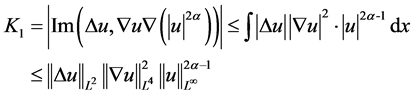
由(2.12)式即得
，
同理，对
做估计
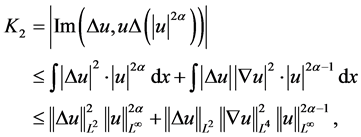
由(2.12)式得到
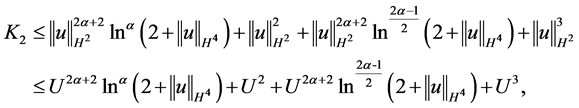
利用不等式
，对
做估计有
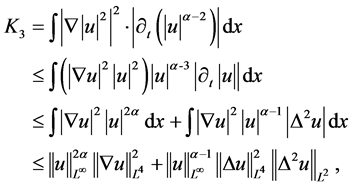
由Gagliardo-Nirenberg不等式
，(3.4)
及(2.12)得到
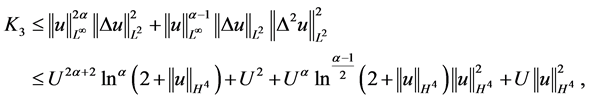
对
进行估计
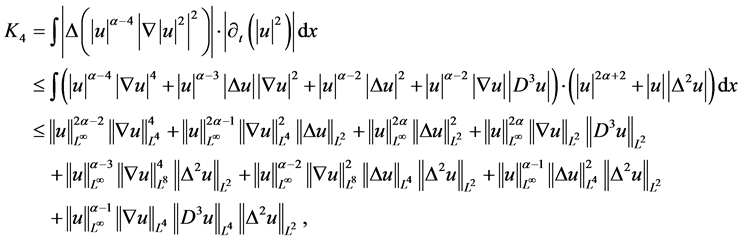
由(2.12)，(2.13)及(3.4)式，即对于上式第5项估计
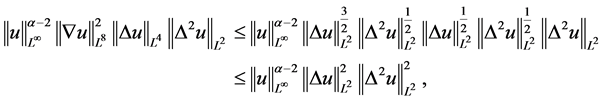
可得
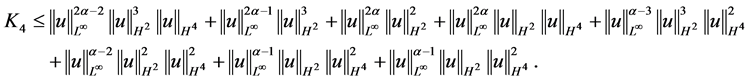
下面对
进行估计
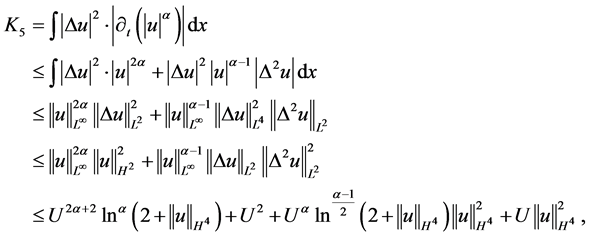
对
进行估计，同理，即有
从而引理3.2.2得证。
定理1.2的证明
首先假设
，且
，由引理3.2.1，需要对下面几个进行估计，运用Hölder不等式及加权的Young不等式得
， (3.5)
利用加权的Young不等式得
(3.6)
同理，则有
(3.7)
又由能量泛函
的定义及(3.5)~(3.7)式有
， (3.8)
再结合(3.3)式和(3.8)式有
(3.9)
由Gronwall不等式得
，从而得出矛盾，并结合定理1.1，进而得出结论，证毕。