摘要:
本文研究多资产期权确定最佳实施边界的问题,建立了多维Black-Scholes方程在多维区域
Ω≅{(s,t)|s∈R+ m,t∈(0,T)} 具有奇异内边界函数向量s=s(t)=(s1(t),...,sm(t)),
0∠t∠T 的数学模型,期权价格函数为未知函数。应用矩阵理论和广义特征函数法获得了期权价格函
数的精确解 u(s,t)。并获得了奇异内边界的指数函数向量表达式
(s1(t),...,sm(t))=(θ1eω1(T-t),...,θmeωm(T-t)) 。证眀了:当任意t∈(0,T) ,数学模型
的解u(s,t)在奇异内边界取区域R+ m:0∠Sj∠∞,j=1,...,m 中的最大值,即
u(s(t),t)=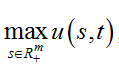 t∈(0,T) ;同时获得了 Black-Scholes方程的自由边界问题A和自由
t∈(0,T) ;同时获得了 Black-Scholes方程的自由边界问题A和自由
边界问题B的精确解和其自由边界的指数函数向量表达式
(s1(t),...,sm(t))=(θ1eω1(T-t),...,θmeωm(T-t)) ,问题A和问题B的自由边界与奇异内边界
重合。从而指数函数向量表达式
s(t)=(s1(t),...,sm(t))=(θ1eω1(T-t),...,θmeωm(T-t)) 为最佳实施边界。指数函数向量
(s1(t),...,sm(t))=(θ1eω1(T-t),...,θmeωm(T-t))
满足条件 ,
,
k=1,...,m;且有ωk 的计算公
式 ;公式表明ωk,k=1,...,m 由多维
;公式表明ωk,k=1,...,m 由多维
Black-Scholes方程中出现的所有参数akj ,qj ,r 唯一确定。
Abstract:
In this paper, we study the problem of determining the optimal implementation boundary
of multi- asset option, and establish a mathematical model of multidimensional Black-Scholes
equation with singular inner boundary function vector
s=s(t)=(s1(t),...,sm(t)),0∠t∠T , In multi-dimension region Ω≅{(s,t)|s∈R+ m,t∈(0,T)}
the option price function is an unknown function. The exact solution u(s,t) of the mathem-
atical model is obtained by using the matrix theory and the generalized characteristic function
method. And the exponential function vector expression of the singular inner boundary is ob-
tained (s1(t),...,sm(t))=(θ1eω1(T-t),...,θmeωm(T-t)) . It is demonstrated that: when any
t∈(0,T) ,the maximum value 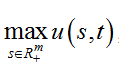 of the solution u(s,t) of the region
of the solution u(s,t) of the region
R+ m:0∠Sj∠∞,j=1,...,m is obtained on the singular boundary, namely u(s(t),t)=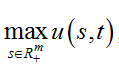 .
.
The free boundary problem A and free boundary problem B of Black-Scholes equation are solved.
The free boundary of problem A and B is expressed by the function vector
R+ m:0∠Sj∠∞, j=(s1(t),...,sm(t))=(θ1eω1(T-t),...,θmeωm(T-t))1,...,m .
The free boundary of the problem A and problem B coincides with the singular inner boundary. So
the vector expression of the exponential function is the best implementation of the boundary. The
exponential function vector (s1(t),...,sm(t))=(θ1eω1(T-t),...,θmeωm(T-t)) satisfies
the condition ,k=1,...,m; and ωk is calculated
,k=1,...,m; and ωk is calculated
by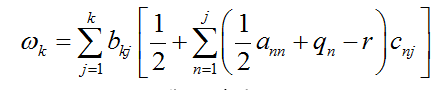 ; the formula shows that ωk is only determined by all
; the formula shows that ωk is only determined by all
the parameters appearing in the multidimensional Black-Scholes equation.
1. 引言
期权是风险管理的核心工具,姜礼尚 [1] 对期权定价理论作了系统深入的阐述,利用偏微分方程理论和方法对期权理论作深入的定性和定量分析,特别对美式期权展开了深入的讨论。美式期权合约中具有提前实施的条款,因此最佳实施边界的确定对于美式期权具有特殊意义。在美式期权定价研究中,姜礼尚 [1] 建立了Black-Scholes方程的自由边界问题,对最佳实施边界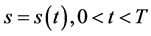 作了很多深入的研究,得到很多重要的结论。其中包括
作了很多深入的研究,得到很多重要的结论。其中包括 的位置,
的位置, 的单调性,
的单调性, 的上下界以及
的上下界以及 的凸性等,并给出了
的凸性等,并给出了 在
在 附近的渐近表达式。这些结果增加了对最佳实施边界的认识,对美式期权定价的数值计祘产生了重要的影响。期权定价问题历来是金融经济学中的重要研究课题之一 [1] - [8] ,多年来,众多经济学者与研究人员对这一问题进行不断深入的研究,但是这些研究大多是围绕具有单个资产的期权进行的。多资产期权在现代金融交易市场中占有重要的地位,研究多资产(或单个资产)期权定价模型大多是围绕数值解法进行的 [9] - [21] ,姜礼尚 [1] 建立了关于期权价格函数
附近的渐近表达式。这些结果增加了对最佳实施边界的认识,对美式期权定价的数值计祘产生了重要的影响。期权定价问题历来是金融经济学中的重要研究课题之一 [1] - [8] ,多年来,众多经济学者与研究人员对这一问题进行不断深入的研究,但是这些研究大多是围绕具有单个资产的期权进行的。多资产期权在现代金融交易市场中占有重要的地位,研究多资产(或单个资产)期权定价模型大多是围绕数值解法进行的 [9] - [21] ,姜礼尚 [1] 建立了关于期权价格函数 的多维Black-Scholes方程
的多维Black-Scholes方程
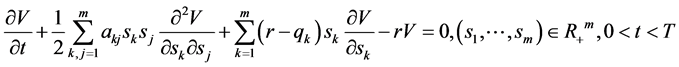 (01)
(01)
其中矩阵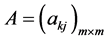 为实对称非负矩阵。研究关于方程(01)的多资产期权的数学模型。
为实对称非负矩阵。研究关于方程(01)的多资产期权的数学模型。
由于
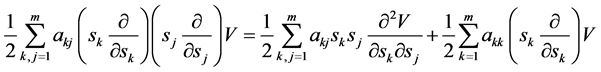 (02)
(02)
故方程(01)可改记为
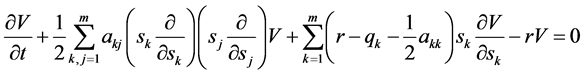 (03)
(03)
本文研究多资产期权确定最佳实施边界的问题,建立了多维Black-Scholes方程在多维区域 具有奇异内边界函数向量
具有奇异内边界函数向量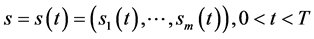 的数学模型,期权价格函数
的数学模型,期权价格函数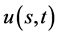 为未知函数。应用矩阵理论和广义特征函数法获得了数学模型的精确解
为未知函数。应用矩阵理论和广义特征函数法获得了数学模型的精确解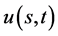 。并获得了奇异内边界的指数函数向量表达式
。并获得了奇异内边界的指数函数向量表达式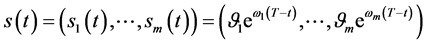 。证眀了:当任意
。证眀了:当任意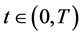 ,数学模型的解
,数学模型的解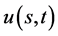 在奇异内边界取
在奇异内边界取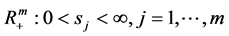 中的最大值,即
中的最大值,即 ;同时获得了Black-Scholes方程的自由边界问题A和自由边界问题B的精确解和其自由边界的指数函数向量表达式
;同时获得了Black-Scholes方程的自由边界问题A和自由边界问题B的精确解和其自由边界的指数函数向量表达式 ,问题A和问题B的自由边界与奇异内边界重合。从而指数函数向量表达式
,问题A和问题B的自由边界与奇异内边界重合。从而指数函数向量表达式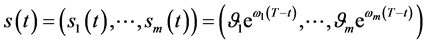 为最佳实施边界。指数函数向量
为最佳实施边界。指数函数向量 ,满足条件
,满足条件 ;且有
;且有 的计算公式
的计算公式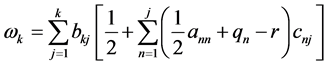 ;公式表明
;公式表明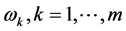 由多维Black-Scholes方程中出现的所有参数
由多维Black-Scholes方程中出现的所有参数 ,
, ,
,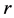 唯一确定。
唯一确定。
2. 主要结果
2.1. 多资产期权的数学模型I的研究
引入记号
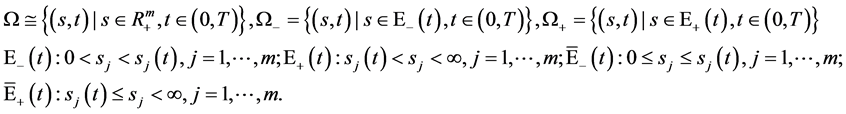
数学模型I (多维Black-Scholes方程具有奇异内边界的终值问题):
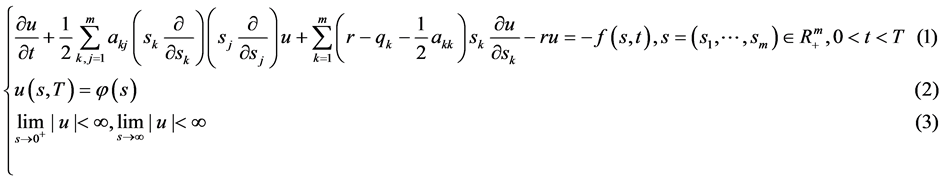
数学模型I是关于多资产期权的数学模型,它是多维Black-Scholes方程在区域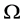 具有奇异内边界
具有奇异内边界 ,
,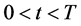 的终值问题,未知函数
的终值问题,未知函数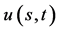 为期权价格函数。
为期权价格函数。
其中:方程的自由项为
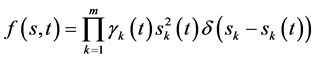 (4)
(4)
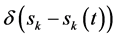 为狄拉克
为狄拉克 -函数;
-函数; 为
为 维狄拉克
维狄拉克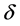 -函数;
-函数; ,
, 为实对称非负矩阵。
为实对称非负矩阵。
数学模型I.1 (多维Black-Scholes方程的终值问题):
 (5)
(5)
数学模型I.2 (多维Black-Scholes方程具有奇异内边界和齐次终值条件的终值问题):
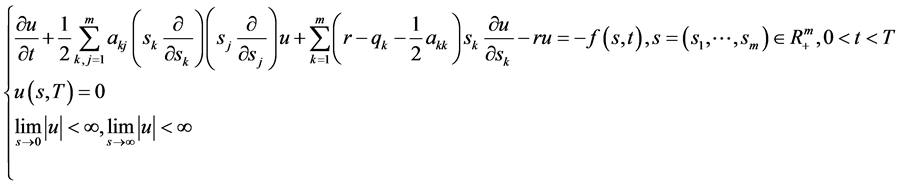 (6)
(6)
2.1.1. Black-Scholes方程数学模型I的求解
记偏微分算子
 (7)
(7)
先考虑m维Euler方程在半无界区域 的特征值问题I
的特征值问题I
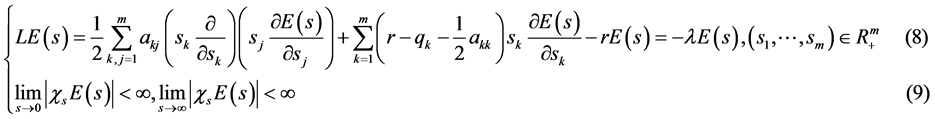
为求解特征值问题I我们建立了引理1.1~引理1.6。
引理1.1:设 为正定矩阵,则存在正线下三角矩阵
为正定矩阵,则存在正线下三角矩阵 满足
满足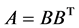 且分解是唯一的;且有
且分解是唯一的;且有
1) 正线下三角矩阵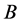 的行列式
的行列式 ,
,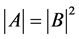 ;
;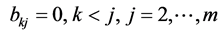 ;
;
2) 由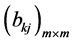 唯一确定
唯一确定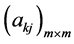 ;由
;由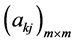 唯一确定
唯一确定 ;
;
3) 记 ,则
,则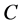 为正线上三角矩阵,
为正线上三角矩阵,
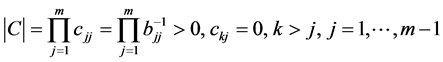 ;由
;由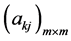 唯一确定
唯一确定 ;
;
4) 记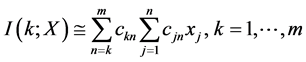 ,
,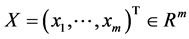 ;则当
;则当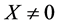 时,有
时,有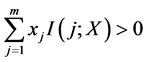 。从而当
。从而当 ,
, ,有
,有 ;
;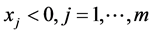 ,有
,有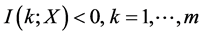 。
。
证明:由矩阵理论 [22] 即知存在正线下三角矩阵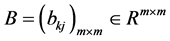 满足
满足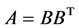 且分解是唯一的。由
且分解是唯一的。由 有
有 。
。
正线下三角矩阵 ,正线下三角矩阵
,正线下三角矩阵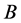 的行列式
的行列式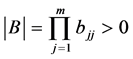 ,且
,且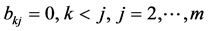 ;
; 的转置矩阵
的转置矩阵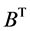 为正线上三角矩阵。
为正线上三角矩阵。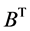 的逆矩阵
的逆矩阵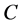 为正线上三角矩阵。
为正线上三角矩阵。 。
。
下证4)由于 为正线上三角矩阵,即有
为正线上三角矩阵,即有 和
和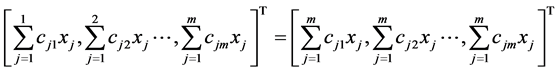 ;从而有
;从而有
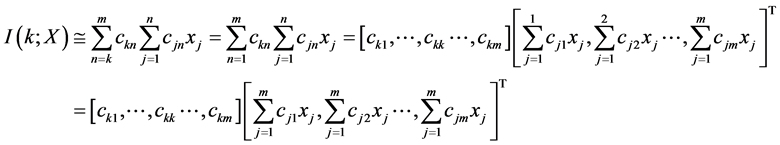
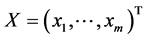 为列向量,应用分块矩阵的乘法运算即有
为列向量,应用分块矩阵的乘法运算即有
从而有
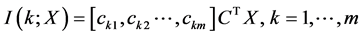 (10)
(10)
由于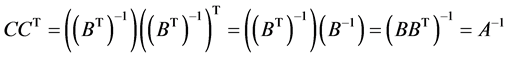 即有
即有
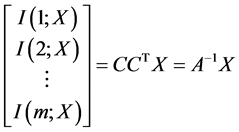 (11)
(11)
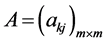 为正定矩阵,则
为正定矩阵,则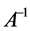 为正定矩阵,
为正定矩阵,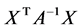 为正定二次齐式,从而有
为正定二次齐式,从而有
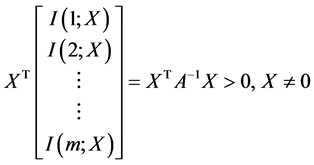 (12)
(12)
 (13)
(13)
由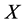 的任意性,分别令
的任意性,分别令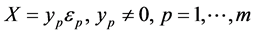 ,
,
其中 。
。
由(13)式即有
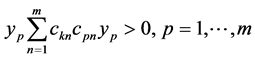
即
从而
 (14)
(14)
再记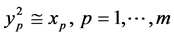 ;有
;有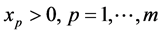 和
和
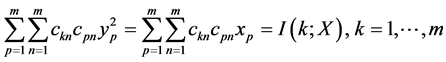 (15)
(15)
由(14),(15)两式即有:当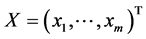 ,
,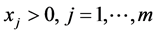 ,有
,有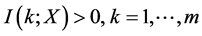 ;显然也有:当
;显然也有:当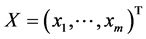 ,
, ,有
,有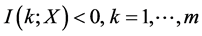 。引理证毕。
。引理证毕。
记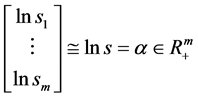 ,作
,作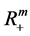 到
到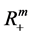 的线性变换
的线性变换
 (16)
(16)
记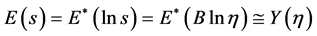 (17)
(17)
引理1.2:若 ,则有
,则有
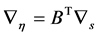 (18)
(18)
其中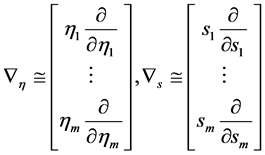 为向量变系数偏微分算子。
为向量变系数偏微分算子。
证明(16)式即
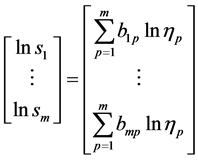 (19)
(19)
由(17)式即有
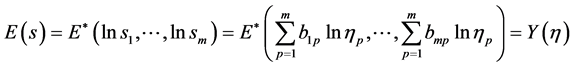 (20)
(20)
由复合函数的求导法则
 (21)
(21)
从而
即(18)式成立。引理证毕。
m维Euler方程在半无界区域 的特征值问题II
的特征值问题II

其中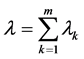 ,
, (24)
(24)
引理1.3:若 ,则特征值问题I中方程(8)与特征值问题II中方程(22)等价。
,则特征值问题I中方程(8)与特征值问题II中方程(22)等价。
证明:由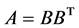 ,有
,有
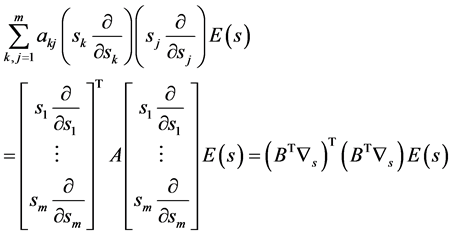 (25)
(25)
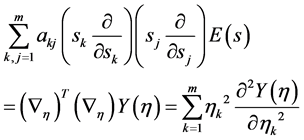 (26)
(26)
记 ,由引理1.1矩阵
,由引理1.1矩阵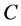 为正线上三角矩阵。
为正线上三角矩阵。
由(18)式有
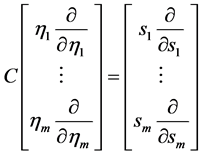 (27)
(27)
由矩阵乘法
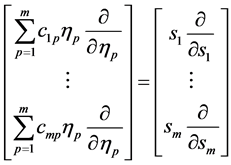 (28)
(28)
从而
 (29)
(29)
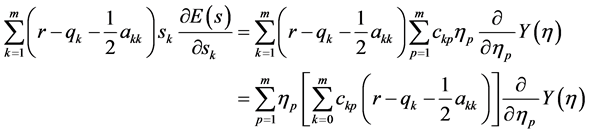 (30)
(30)
由于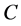 为正线上三角矩阵有
为正线上三角矩阵有

记
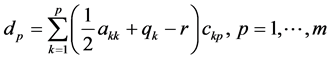 (31)
(31)
即有
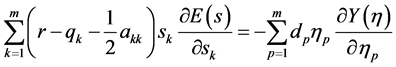 (32)
(32)
由(26),(32)两式即知方程(8)与方程(22)等价。引理证毕。
引理1.4:特征值问题II的特征值
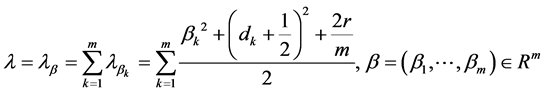 (33)
(33)
所对应的特征函数为
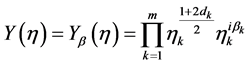 (34)
(34)
且有
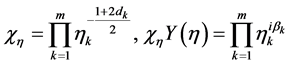 (35)
(35)
证明:容易求解特征值问题II:由分离变量法令
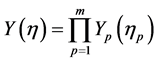 (36)
(36)
 (37)
(37)
再令
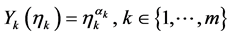 (38)
(38)

 (39)
(39)
 (40)
(40)
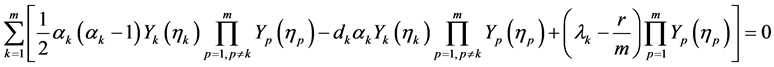
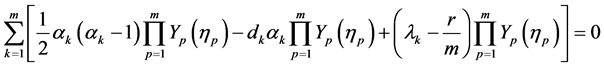 (41)
(41)
 (42)
(42)
若(42)式成立则(41)式成立;特征函数
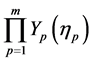
不恒为零,由(42)推出
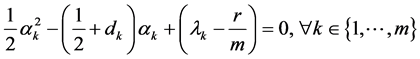 (43)
(43)
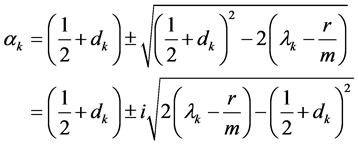
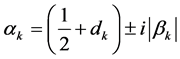
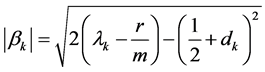
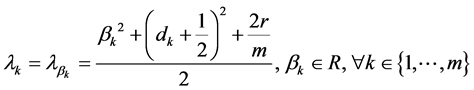 (44)
(44)
 (45)
(45)
 (46)
(46)
 (47)
(47)
 (48)
(48)
由(48)式即有(23)式成立。引理证毕。
由(16)和(17)式换回原变量即得特征值问题I的特征函数
 (49)
(49)
且
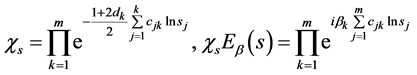 (50)
(50)
 (51)
(51)
由(51)式即有(9)式成立。于是得到
引理1.5:特征值问题I的特征值
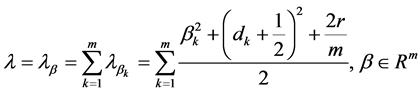 (52)
(52)
所对应的特征函数为
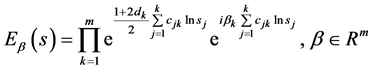 (53)
(53)
引理1.6:特征值问题I的特征函数系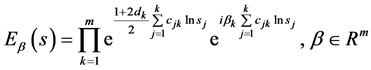 是半无界区域
是半无界区域 带权函数
带权函数 的完备正交系;正交关系即
的完备正交系;正交关系即
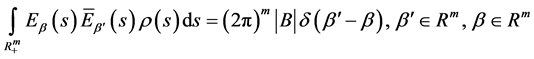 (54)
(54)
证明:由于
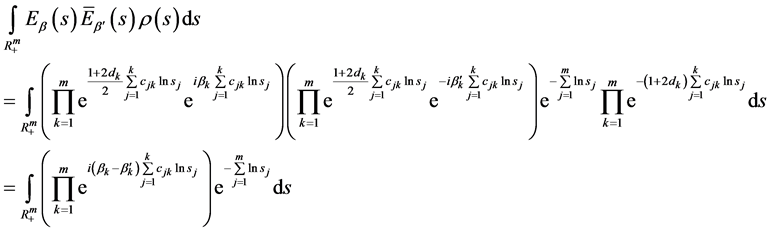 (55)
(55)
引入变量代换
 (56)
(56)
由于行列式
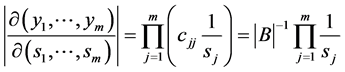
即有变量替换的雅可比行列式
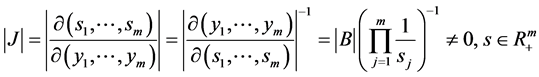 (57)
(57)
由多重积分变量替换公式,即有

 (58)
(58)
(58)式即(54)式。引理证毕。
由引理1.5与引理1.6的结论可以引入广义特征函数法 [23] [24] 求解 数学模型I。
不妨设解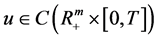 ,将其表为特征函数的积分形式
,将其表为特征函数的积分形式
 (59)
(59)
将上式两边乘以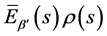 再关于变量
再关于变量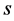 在
在 积分,利用正交关系(54)则有
积分,利用正交关系(54)则有
 (60)
(60)
得到
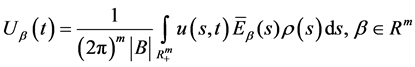 (61)
(61)
将方程中的自由项 也表为特征函数的积分形式
也表为特征函数的积分形式
 (62)
(62)
由(61)即有
 (63)
(63)
应用 -函数的积分性质即得
-函数的积分性质即得
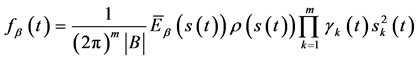 (64)
(64)
含参变量积分与算子 的运算交换次序即有
的运算交换次序即有
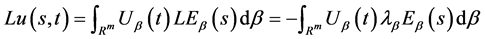 (65)
(65)
 (66)
(66)
由(2)即有
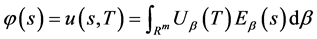 (67)
(67)
 (68)
(68)
将(62),(65),(66)代入方程(1)即有
 (69)
(69)
由特征函数系的完备正交性即有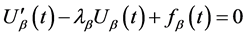 ,再由(68)式即得
,再由(68)式即得
非齐次常微分方程的终值问题
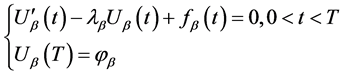 (70)
(70)
用常数变易法得到非齐次常微分方程的终值问题的解为
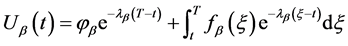 (71)
(71)
将上式代入(59)式即得
 (72)
(72)
将 的表达式(52),(53)代入(72),并记
的表达式(52),(53)代入(72),并记
 (73)
(73)
 (74)
(74)
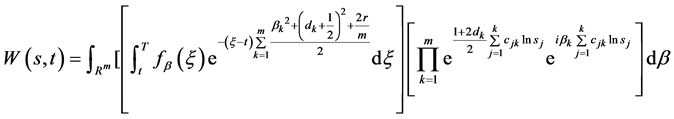 (75)
(75)
其中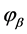 由(68),
由(68),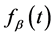 由(64)确定。
由(64)确定。
由(74)式即有
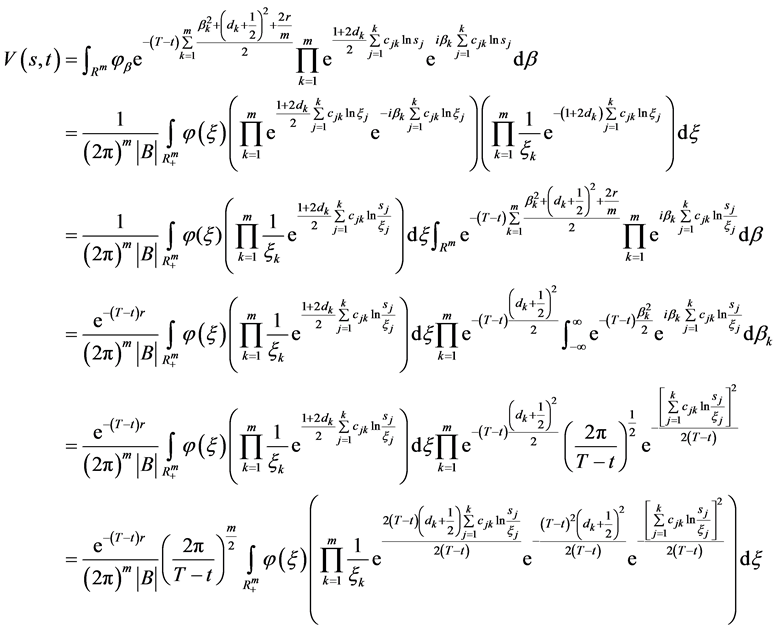

于是有
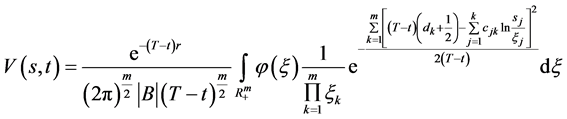 (76)
(76)
将 的表达式代入(64)式,化简即得
的表达式代入(64)式,化简即得
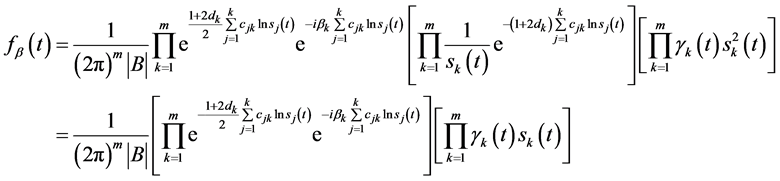 (77)
(77)
将(77)代入(75)式,并化简
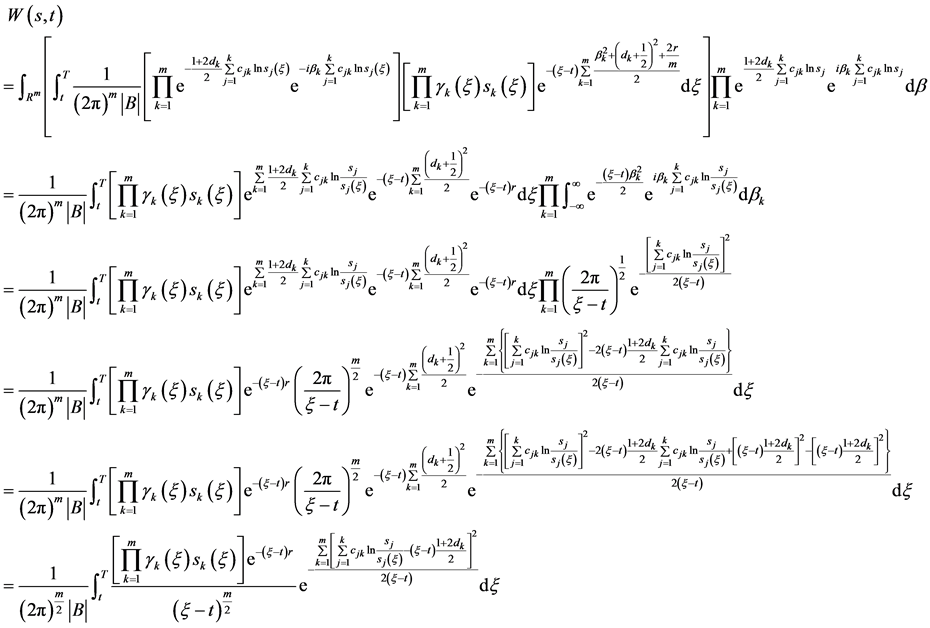
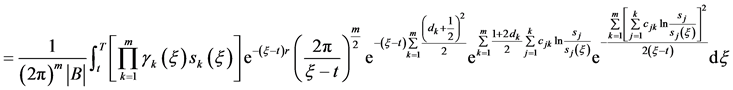
即得
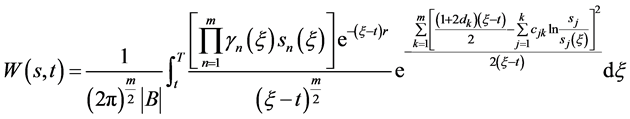 (78)
(78)
定理1 (数学模型I解的存在定理):若
1) 为正定对称矩阵,
为正定对称矩阵,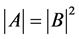 ;
;
2)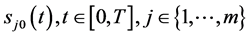 为充分光滑的单调函数;
为充分光滑的单调函数;
3) 。
。
则数学模型I有精确解:
 (79)
(79)
 (80)
(80)
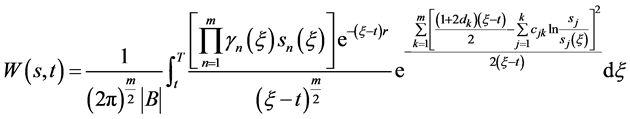 (81)
(81)
且数学模型I.1的解 由(80)式给出,数学模型I.2的解
由(80)式给出,数学模型I.2的解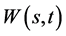 由(81)式给出。
由(81)式给出。
2.1.2. 多维Black-Scholes方程奇异内边界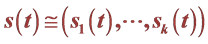 的确定
的确定
数学模型II (多维Black-Scholes方程确定奇异内边界的终值问题):
求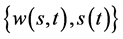 ,使其满足
,使其满足

定理2 (数学模型II解的存在定理):若
1) 为正定对称矩阵;
为正定对称矩阵;
2)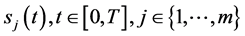 为充分光滑的单调函数;
为充分光滑的单调函数;
3)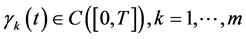 。
。
则数学模型II有连续有界的精确解

数学模型II有解的相容性条件是
 (89)
(89)
其中
 (90)
(90)
 (91)
(91)
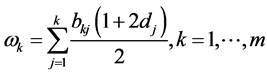 (92)
(92)
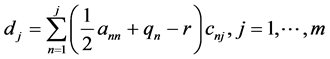 (93)
(93)
证明:由定理1(数学模型I解的存在定理)的结论,(81)式给出的 已满足条件(82) (83) (85)三式,让
已满足条件(82) (83) (85)三式,让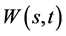 满足条件(84)式去确定奇异内边界
满足条件(84)式去确定奇异内边界 。
。
将(81)式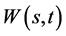 记为
记为
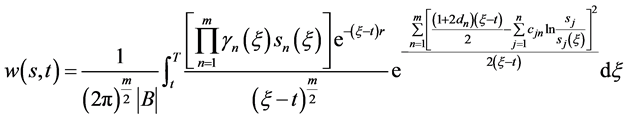 (94)
(94)
由(94)式对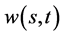 关于自变量
关于自变量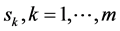 求偏导,由复合函数的求导法则有
求偏导,由复合函数的求导法则有
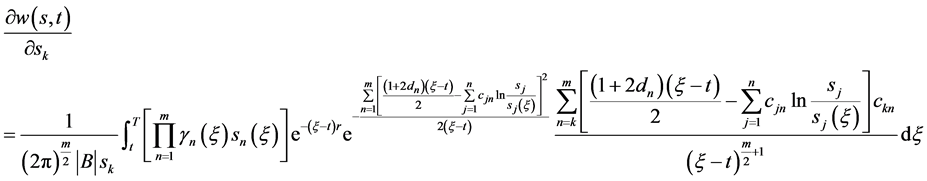 (95)
(95)
若令
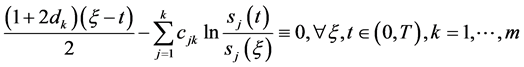 (96)
(96)
则

即有
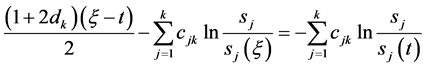 (97)
(97)
将(97)式代入(95)式即有
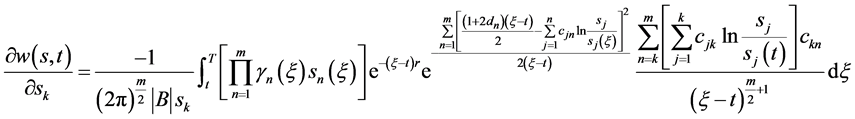 (98)
(98)
下面建立引理2.1~引理2.4来完成定理2的证明。
引理2.1:条件(96)成立,则有
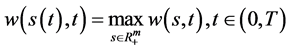 (99)
(99)
和
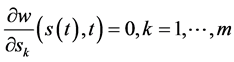 (100)
(100)
证明:若条件(96)成立,则有(98)成立。由(98)式易知(100)式成立。
由(98)即得到対任意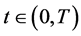 有
有
1) 当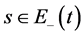 有
有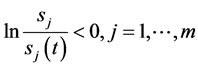
由引理1.1的结论4)即有即有:当 ,有
,有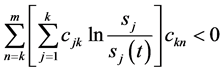 成立,从而
成立,从而
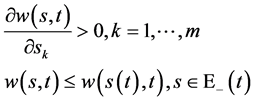 (101)
(101)
2) 当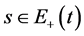 有
有
由引理1.1中结论4)即有:当 ,有
,有 成立,从而
成立,从而
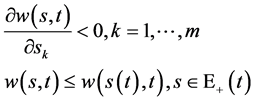 (102)
(102)
从而(99)式成立。引理证毕。
引理2.2:条件
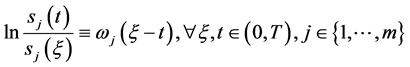 (103)
(103)
成立的充要条件为
 (104)
(104)
证明:1) 必要性,若(103)成立,由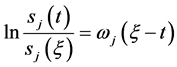 即有
即有
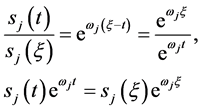 (105)
(105)
记
 (106)
(106)
由(105)式有
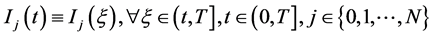 (107)
(107)
让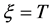 即有
即有
 (108)
(108)
干是有(104)式成立。
2) 充分性,若(104)式成立,即有

即(103)成立。引理证毕。
引理2.3:当条件
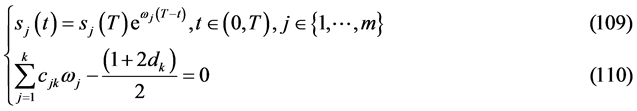
成立时,则条件(96)成立,从而有 。
。
证明:由(109)式则有
 (111)
(111)
再由(110)式即有
 (112)
(112)
即条件(96)成立,由引理2.1即有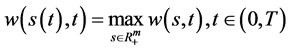 成立。引理证毕。
成立。引理证毕。
引理2.4:未知数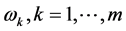 的线性方程组(110)的解为
的线性方程组(110)的解为
 (113)
(113)
证明:线性方程组(110)写成矩阵形式即为
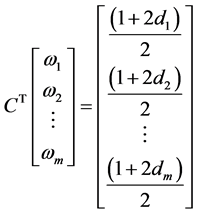 (114)
(114)
由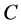 矩阵的定义即有
矩阵的定义即有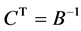 ,从而
,从而
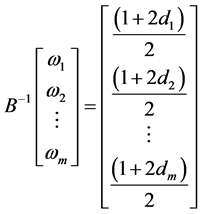 (115)
(115)
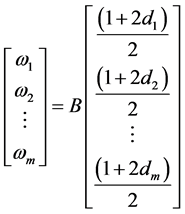 (116)
(116)
由矩阵乘法即得线性方程组(110)的解由(113)式给出。引理证毕。
记
 (117)
(117)
由引理2.1~引理2.4即知:当(117)成立时,有解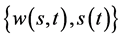 其中
其中 由(94)给出,
由(94)给出,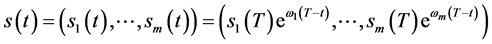 。由(117)式即有(96)成立,由引理2.1即有
。由(117)式即有(96)成立,由引理2.1即有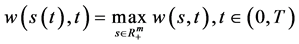 和
和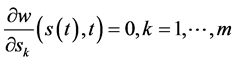 成立。
成立。
由(117)式即有(97)式成立,将(97)代入(94)即有:
 (118)
(118)
再将(117)式代入(118)式,即有
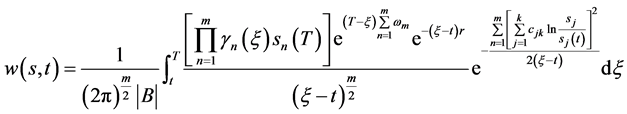 (119)
(119)
引入记号: ,再由(119)即得到
,再由(119)即得到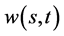 由(87)给出。由(87)式给出的解
由(87)给出。由(87)式给出的解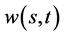 满足条件(84)式和(85)式。从而满足数学模型II,即(87),(88)两式给出了数学模型II的解。由(87)式即知数学模型II有解的相容性条件是(89)式。定理证毕。
满足条件(84)式和(85)式。从而满足数学模型II,即(87),(88)两式给出了数学模型II的解。由(87)式即知数学模型II有解的相容性条件是(89)式。定理证毕。
引入记号

多维开区间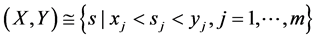 ,多维闭区间
,多维闭区间 。
。
函数的支集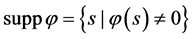 ,支集的闭包
,支集的闭包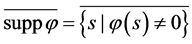 ,记函数集合
,记函数集合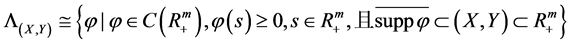 。
。
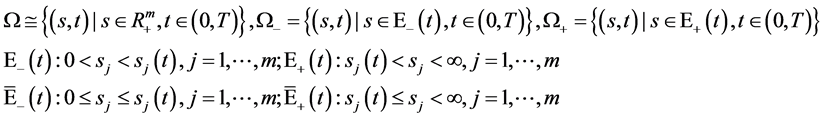
记
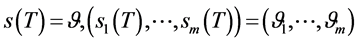 (120)
(120)
 (121)
(121)
定理3(数学模型I.1解的性质定理):若 为正定矩阵,
为正定矩阵, ;则
;则
1) 当 ;数学模型I.1的解
;数学模型I.1的解
 (122)
(122)
满足
 (123)
(123)
和
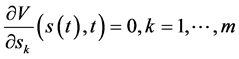 (124)
(124)
其中
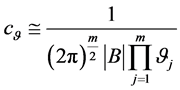 (125)
(125)
2) 当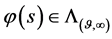 ,则数学模型I.1的解
,则数学模型I.1的解
 (126)
(126)
且解 满足
满足
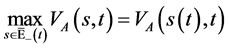 (127)
(127)
3) 当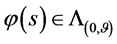 ,数学模型I.1的解
,数学模型I.1的解
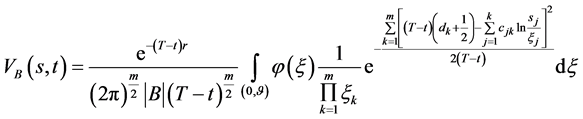 (128)
(128)
且解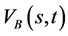 满足
满足
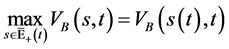 (129)
(129)
证1): 数学模型I.1的解由定理1的(74)式给出,由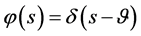 有
有
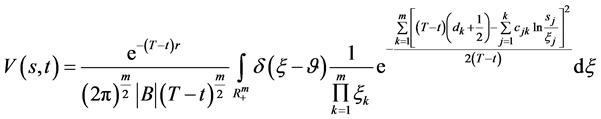 (130)
(130)
应用多维狄拉克 -函数的积分性质即得
-函数的积分性质即得
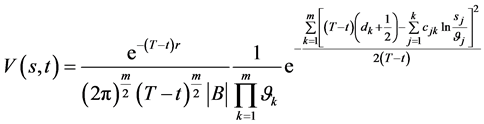 (131)
(131)
引入记号 即有
即有
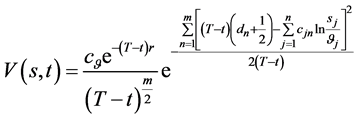 (132)
(132)
由于 线性方程组(110)的解,由(110)即有
线性方程组(110)的解,由(110)即有
 (133)
(133)
由(112)式即有
即有
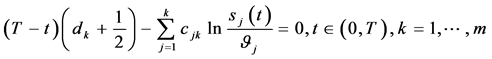 (134)
(134)
由(132)和(134)两式即有
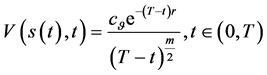 (135)
(135)
由于
 (136)
(136)
从而
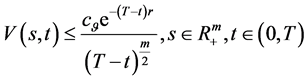 (137)
(137)
故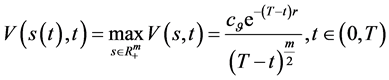 。由(132)对
。由(132)对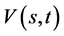 关于
关于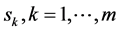 求偏导得到
求偏导得到
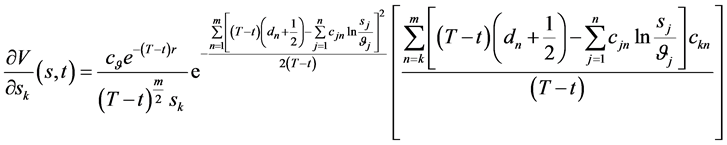 (138)
(138)
 (139)
(139)
由(134),(139)即得(124)。
证2):数学模型I.1的解由定理1的(74)式给出。任意 即有
即有 。
。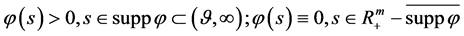 ,故
,故 ,
, 。于是(74)式中积分的积分区域由
。于是(74)式中积分的积分区域由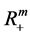 变为
变为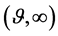 。则数学模型I.1的解
。则数学模型I.1的解
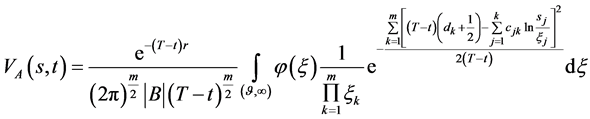 (140)
(140)
由(140)关于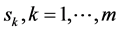 求偏导
求偏导
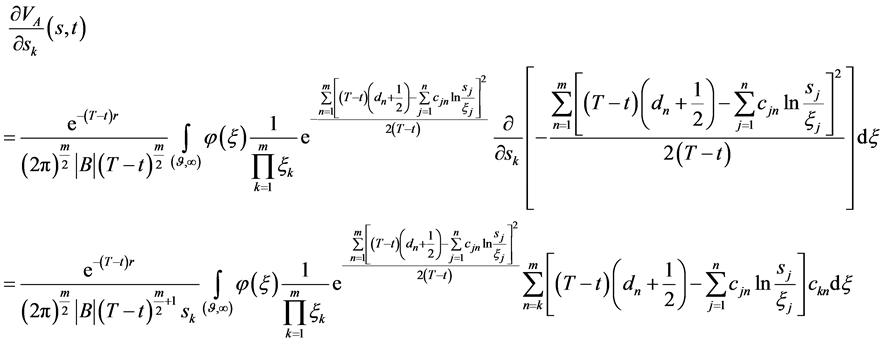
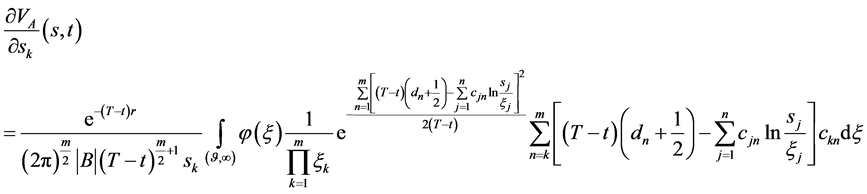 (141)
(141)
当 有
有 ;积分变量
;积分变量 ,有
,有 ;
;
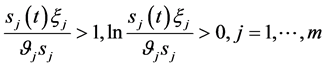 (142)
(142)
又
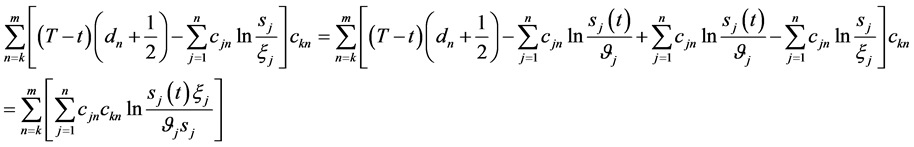 (143)
(143)
记
 ;由(142),有
;由(142),有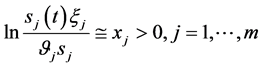 ,引理1.1的结论4)即有
,引理1.1的结论4)即有 ;
;
从而由(143)有
 (144)
(144)
再由(141)即有当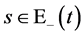 ,
,
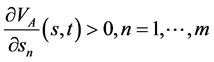 (145)
(145)
当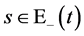 ,
, ,从而有
,从而有 成立。
成立。
证3):当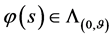 ,由数学模型I.1的解(74)式即有(128)成立。由(128) 式对
,由数学模型I.1的解(74)式即有(128)成立。由(128) 式对 关于
关于 求偏导即有
求偏导即有
 (146)
(146)
当 ,有
,有 ,
,
引理1.1的结论4)即有
由(146)即有:当 ,
,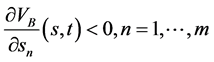 。当
。当 ,
,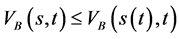 ,从而有
,从而有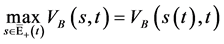 成立。定理证毕。
成立。定理证毕。
2.2. 关于多维Black-Scholes方程的自由边界问题的研究
由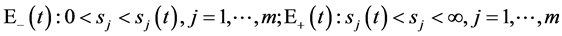
即有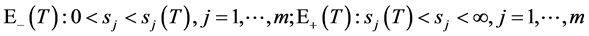
即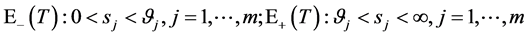
即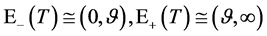
下面分别讨论关于多维Black-Scholes方程在 的自由边界问题A和在
的自由边界问题A和在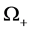 的自由边界问题B。
的自由边界问题B。
自由边界问题A (关于多维Black-Scholes方程在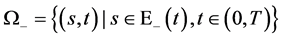 的自由边界问题):求
的自由边界问题):求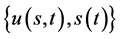 ,使其满足
,使其满足
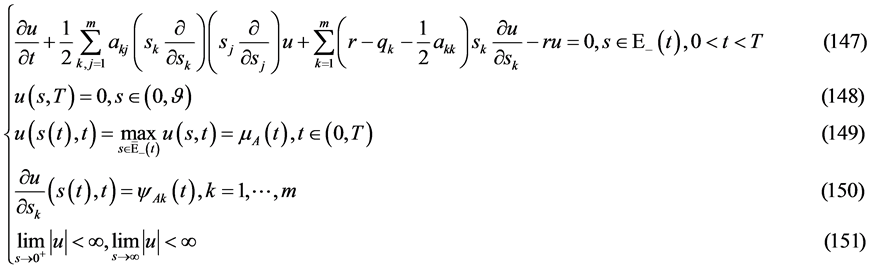
定理4 (自由边界问题A多解性定理):若
1)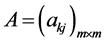 为正定矩阵;
为正定矩阵;
2) ;
;
则自由边界问题A的有解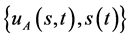 ,自由边界为
,自由边界为
 (152)
(152)
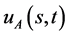 具有多解性,第一解:
具有多解性,第一解:
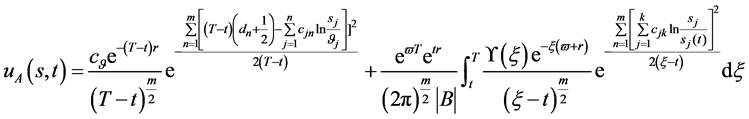 (153)
(153)
有解的相容性条件
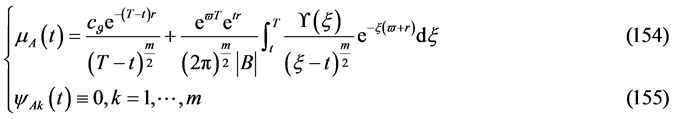
第二解:
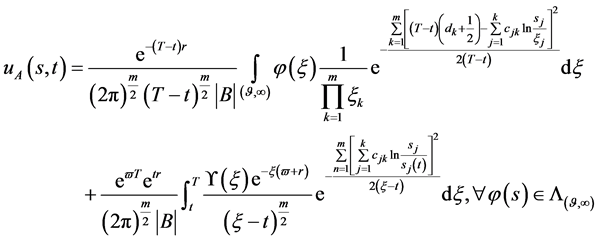 (156)
(156)
有解的相容性条件
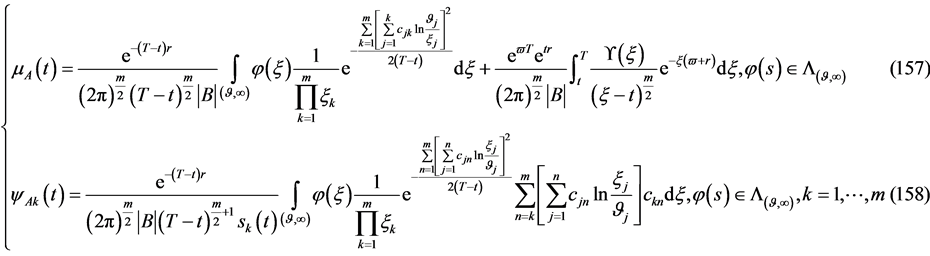
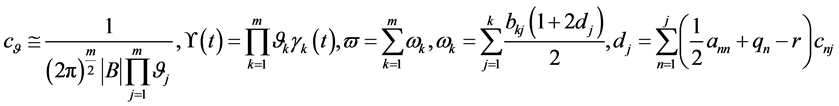 (159)
(159)
证明:当 由定理2的(87)式给出的解滿足齐次方程(147),故由(153)式和(156)式给出的解滿足齐次方程(147)。再由定理2,定理3的结论即知定理4成立。由(112),(152)两式即有
由定理2的(87)式给出的解滿足齐次方程(147),故由(153)式和(156)式给出的解滿足齐次方程(147)。再由定理2,定理3的结论即知定理4成立。由(112),(152)两式即有
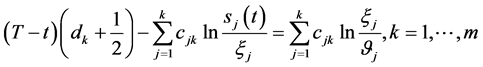 (160)
(160)
推证相容性条件(158),由(141),(160)两式即得。定理证毕。
附注1:定理4中的笫二解对在函数集合 任意给定的
任意给定的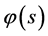 都有由(156)式给出的解
都有由(156)式给出的解 与之对应,即得到了一个解族
与之对应,即得到了一个解族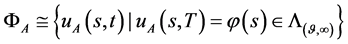 。
。
自由边界问题B (关于多维Black-Scholes方程在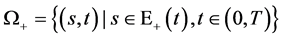 的自由边界问题):求
的自由边界问题):求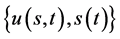 ,使其满足
,使其满足
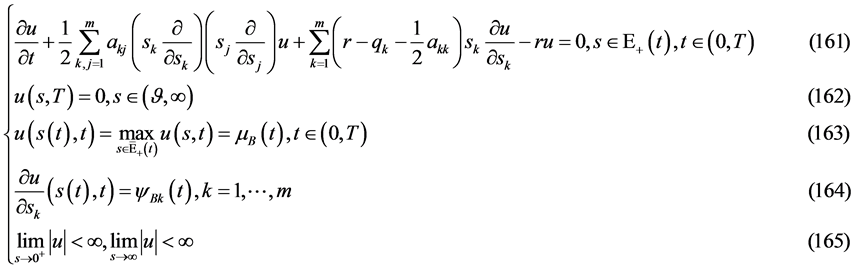
定理5 (自由边界问题B多解性定理):若
1) 为正定矩阵;
为正定矩阵;
2)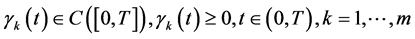 ;
;
则自由边界问题B有解 ,自由边界为
,自由边界为
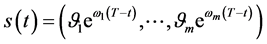 (166)
(166)
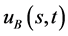 具有多解性,第一解:
具有多解性,第一解:
 (167)
(167)
有解的相容性条件
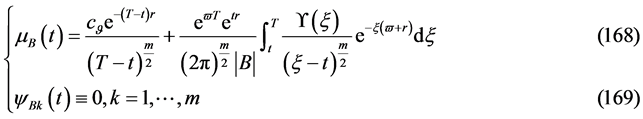
第二解:
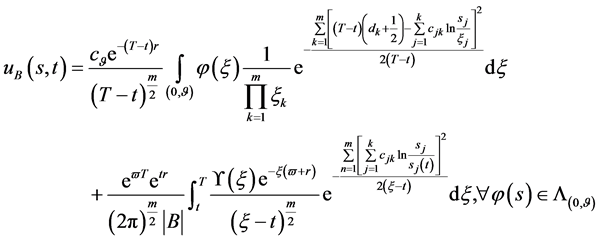 (170)
(170)
有解的相容性条件
 (171)
(171)
 (172)
(172)
其中
 (173)
(173)
证明:当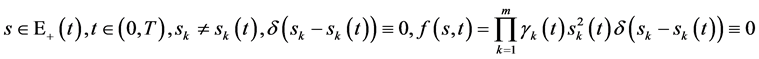 由定
由定
理2的(87)式给出的解滿足齐次方程(161),故由(167)式和(170)式给出的解滿足齐次方程(161)。再由定理2,定理3的结论即知定理5成立。推证相容性条件(172)由(146) (160)两式即得。定理证毕。
附注2:定理5中的笫二解对在函数集合 任意给定的
任意给定的 都有由(170)式给出的解
都有由(170)式给出的解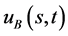 与之对应,即得到了一个解族
与之对应,即得到了一个解族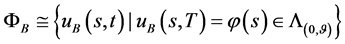 。
。
2.3. 数学模型III与自由边界问题A和问题B的关系
数学模型III (多维Black-Scholes方程确定奇异内边界的终值问题):
求 ,使其满足
,使其满足
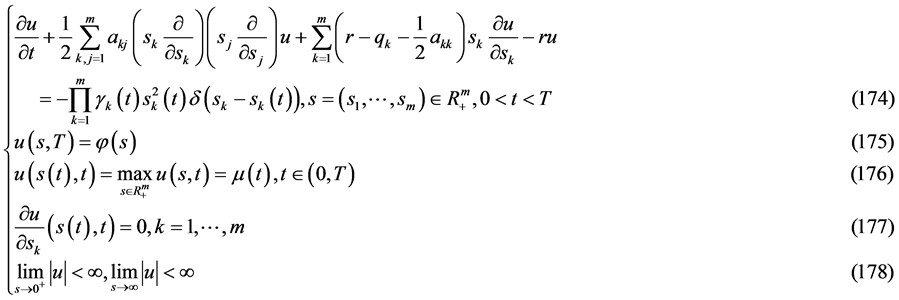
定理6 (奇异内边界与问题A和B的自由边界三线合一定理一):若
1)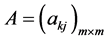 为正定矩阵;
为正定矩阵;
2)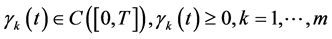 ;
;
3)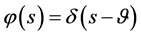 ;
;
4)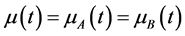 ;
;
5) 。
。
则数学模型III与问题A和问题B有相同表达式的解
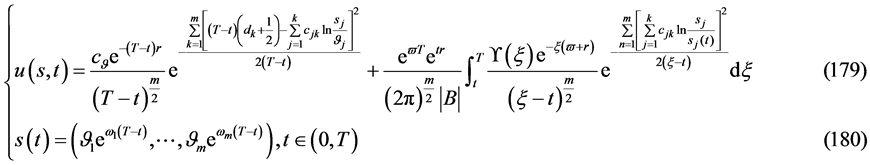
有解的相容性条件
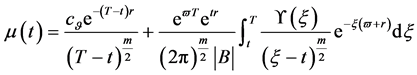 (181)
(181)
其中
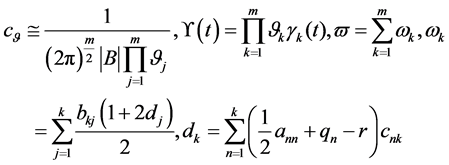 (182)
(182)
数学模型III的奇异内边界与问题A和问题B的自由边界三曲线重合成同一指数函数向量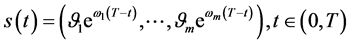 ;数学模型III的解函数是问题A和B的解函数的共同连续开拓,即
;数学模型III的解函数是问题A和B的解函数的共同连续开拓,即
 (183)
(183)
定义2:若 ,
,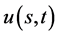 由(183)定义,称
由(183)定义,称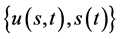 为数学模型III与问题A和问题B的一致相容解。
为数学模型III与问题A和问题B的一致相容解。
定理7 (奇异内边界与问题A和B的自由边界三线合一定理二):若
1)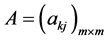 为正定矩阵;
为正定矩阵;
2)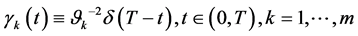 ;
;
3)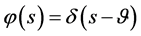 ;
;
4)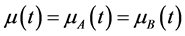 ;
;
5) 。
。
则数学模型III与问题A和问题B的一致相容解
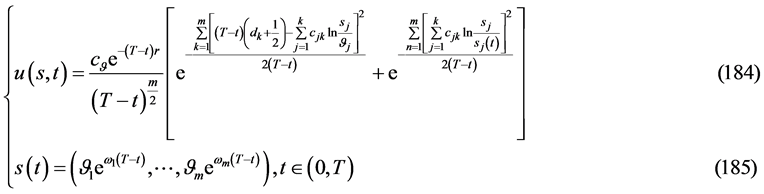
有解的相容性条件
 (186)
(186)
 (187)
(187)
定理8 (奇异内边界与问题A和问题B的自由边界三线合一定理三):若
1)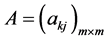 为正定矩阵;
为正定矩阵;
2) ;
;
3)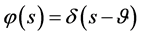 ;
;
4)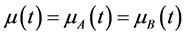 ;
;
5)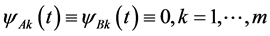 。
。
则数学模型III与问题A和问题B的一致相容解

有解的相容性条件
 (190)
(190)
其中
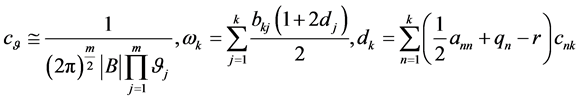 (191)
(191)
由定理6,定理7,定理8给出的一致相容解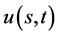 满足条件
满足条件
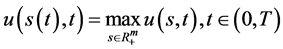 (192)
(192)
即一致相容解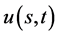 在任意时刻
在任意时刻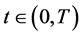 在
在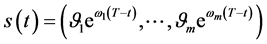 取
取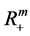 中的最大值
中的最大值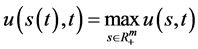 ,从而称
,从而称 为最佳实施边界。
为最佳实施边界。
定理9 (多资产期权最佳实施边界定理):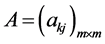 为正定矩阵,则期权价格函数
为正定矩阵,则期权价格函数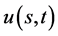 在任意时刻
在任意时刻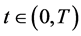 在
在
 取
取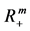 中的最大值
中的最大值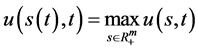 ,多资产期权最佳实施边界为指数函数向量
,多资产期权最佳实施边界为指数函数向量
 (193)
(193)
满足
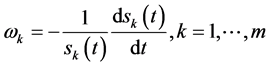 (194)
(194)
且有 的计算公式
的计算公式
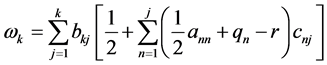 (195)
(195)
公式(195)表明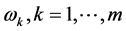 由多维Black-Scholes方程中出现的所有参数
由多维Black-Scholes方程中出现的所有参数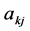 ,
,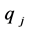 ,
,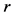 唯一确定。
唯一确定。
证明:由定理6,定理7,定理8即知期权价格函数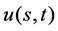 在任意时刻
在任意时刻 在
在
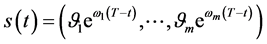 取
取 中的最大值
中的最大值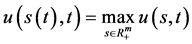 ,从而多资产期权最佳实施边界为指数函数向量(193)。关于
,从而多资产期权最佳实施边界为指数函数向量(193)。关于 的计算公式(93)式代入
的计算公式(93)式代入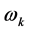 的计算公式(92)式即得
的计算公式(92)式即得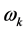 的计算公式(195),由引理1.1即知
的计算公式(195),由引理1.1即知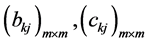 皆由
皆由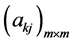 唯一确定,从而
唯一确定,从而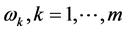 由多维Black-Scholes方程中出现的所有参数
由多维Black-Scholes方程中出现的所有参数 ,
, ,
, 唯一确定。定理证毕。
唯一确定。定理证毕。
3. 结论
指数函数向量 为多资产期权的最佳实施边界,满足条件
为多资产期权的最佳实施边界,满足条件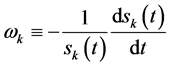 ;且
;且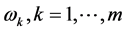 由多维Black-Scholes方程中出现的所有参数
由多维Black-Scholes方程中出现的所有参数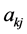 ,
,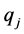 ,
,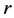 唯一确定。
唯一确定。