1. 引言
机器人行走过程中，可被认为是多自由度的并联系统。足力对机身平衡起着决定性作用，尤其是当机器人在不规则路面及刚度较小路面行走时，足端支撑力的变化会使机器人机身的姿态发生改变，进而影响稳定性。除此之外，足力的变化与机器人腿部运动的柔顺性也密切相关，当足端的运动存在由自由空间到约束空间的转换时，仅采用位置控制将无法满足腿部对运动柔顺性的要求。因此，对足式机器人足力控制的研究必不可少。本文将对四足机器人足力控制方法进行研究，并通过仿真手段进行必要的分析。
2. 基于位置的阻抗控制建模与分析
2.1. 阻抗控制原理
机器人的阻抗控制方法最早由Hogan在1985年提出 [1] 。这种方法的基本思想是，将机器人等效为“质量–弹簧–阻尼”系统，通过此模型建立机器人末端力和末端位置的关系，并通过调节控制器中的惯性、阻尼和刚度参数来调整机器人与环境接触时的动态特性。这种控制方法不是直接地控制机器人末端的接触力，而是通过阻抗模型，间接地通过控制位置来控制末端力。阻抗控制的目的可以表述为参照目标阻抗模型建立机器人末端位置和末端力的动态关系。
机器人末端所受的力与位置偏差之间的关系称为期望阻抗模型，该模型原则上可以是任意函数，但二阶微分方程形式较为常用 [2] 。假定机器人在n(n运6)维空间内操作，X、Xr和F分别为表示末端实际位置、末端期望位置和机器人末端作用力的n × 1维列向量，常用的阻抗模型表达式有如下三种形式：
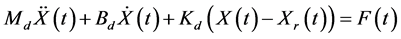(1)
(2)
(3)
其中，Md、Bd和Kd为3 × 3对角阵，分别为期望惯性、期望阻尼和期望刚度值。为实现力跟踪，可将表示力参考值的n × 1维列向量Fr引入阻抗模型，使得目标阻抗演化为力偏差E = Fr− F与X和Xr之间的关系，那么阻抗模型表达式变为
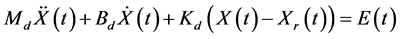(4)
(5)
(6)
阻抗控制按照原理不同分为基于力的阻抗控制和基于位置的阻抗控制。实际应用中，由于难以对机器人的关节力矩进行精确控制，所以应用较为广泛的是基于位置的阻抗控制。这种控制结构由位置控制内环和阻抗控制外环构成，期望位置Xr经过位置闭环后输出末端实际位置，在环境的作用下产生接触力F，这个力经过阻抗控制器后得到位置的修正量∆X，参考轨迹Xr与∆X相加后作为内环的输入，影响机器人末端的实际位置，进而影响接触力。可以看出，位置控制器的响应速度和控制精度将对力控制效果有显著的影响。因此，对位置控制内环进行分析非常必要。
2.2. 机器人腿部关节位置控制建模
随着电力电子技术和计算机技术的发展进步，交流伺服系统已经在高精度速度与位置控制场合占据相当的比例。在几种执行元件中，永磁同步电机(PMSM, Permanent Magnet Synchronous Motor)由于其具有效率高、结构简单和易于维护等特点得到了广泛应用，其组成的运动控制系统具有稳定裕度高且动态特性较好的特点。本文研究的机器人选用永磁同步电机作为执行元件。
永磁同步电机的运动控制系统是典型的位置、速度和电流三环调节系统。分析永磁同步电机时常采用dq坐标系下的数学模型，这种方法可以兼顾系统的稳态特性和动态特性分析 [3] 。首先，做以下几点假定
(1) 不计铁心饱和及铁耗；
(2) 三相电流对称；
(3) 不计涡流和磁滞损耗；
(4) 转子无阻尼绕组，永磁体不计阻尼作用。可以得到dq坐标系下永磁同步电机的电压方程为：
(7)
磁链方程为
(8)
电磁转矩方程为
(9)
力平衡方程为
(10)
式中：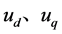
——电机定子d轴、q轴电压；
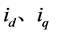——电机定子d轴、q轴电流；
——电机定子直轴、交轴磁链；
——电机定子绕组d轴、q轴电感；
——电机定子绕组电阻；
——永磁体基波磁场在定子绕组中产生的磁链；
——转矩常数；
——电机的电角速度和机械角速度；
——电机的等效惯性负载；
——电机的等效阻尼；
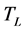——电机的等效负载力矩。
对于面装式永磁同步电机，有：
(11)
其中L为电机定子绕组电感。
在dq坐标系内通过控制矢量电流is的幅值和相位，可以控制电磁转矩，这等同于控制is的两个电流分量iq和id。由电磁转矩方程式(4-9)可以看出，决定电磁转矩的是定子电流的q轴分量即iq。为简化控制方法，若采用d轴电流为零的控制方法，即：
(12)
则定子电流全部用于产生电磁转矩，此时可将面装式永磁同步电机模型等效为他励直流电机模型。由式(7)至式(12)整理并进行Laplace变换可以得出永磁同步电机的数学模型为
(13)
3. 阻抗控制器性能分析
阻抗控制的思想是将机器人等效为具有弹性、阻尼和惯性特性的系统，通过调整这三个特性参数来获得期望的阻抗或导纳特性，影响机器人与环境接触时的动态过程，进而间接地调整机器人与环境的接触力等指标。可以通过分别调整各个参数，获得控制器的输出特性，分析阻抗控制器各参数对机器人动态特性的影响。
3.1. 目标惯性的影响
令Bd= 200 N/(m/s)，Kd= 2500 N/m，Md的值在1 kg~9 kg之间变化，得到位置修正值的响应如图1所示。由图看出，目标惯性仅影响响应的动态过程，而不影响响应的稳态值。在超调产生之前，响应曲线的上升速度随目标惯性的增大略有减小，但调整时间逐渐变小；响应产生超调后，响应曲线的上升速度和调整时间均随着目标惯性的增大而增大。
3.2. 目标阻尼的影响
令Md = 1 kg，Kd = 2500 N/m，Bd的值在30 N/(m/s)~200 N/(m/s)之间变化，得到位置修正值的响应如图2所示。由图看出，显然目标阻尼亦不影响应的稳态值，只对动态响应过程造成影响。随着目标阻尼的减小，响应曲线的上升速度逐渐变快，调整时间逐渐变小，且在阻尼减小到一定程度时产生超调。在实际应用中，应根据机器人工作任务的要求合理地调整目标阻尼值。
3.3. 目标刚度的影响
令Md = 1 kg，Bd = 100 N/(m/s)，Kd的值在50 N/m~2500 N/m之间变化，得到位置修正值的响应如图3所示。可以看出，目标刚度对动态过程影响很微弱，主要影响响应的稳态值。随着Kd的增大，阻抗控制器的稳态输出值越来越小。从物理意义上讲，这相当于两个弹簧串联时相接点的位移随弹簧刚度变
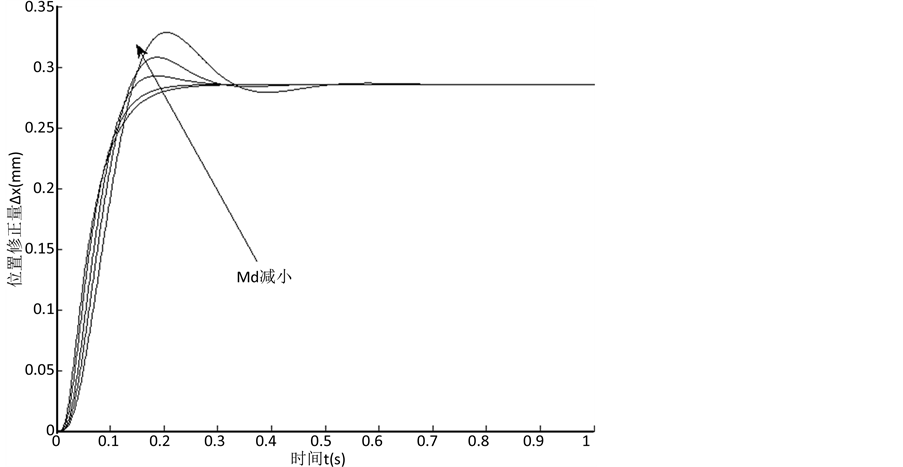
Figure 1. The influence of target inertia
图1. 目标惯性的影响
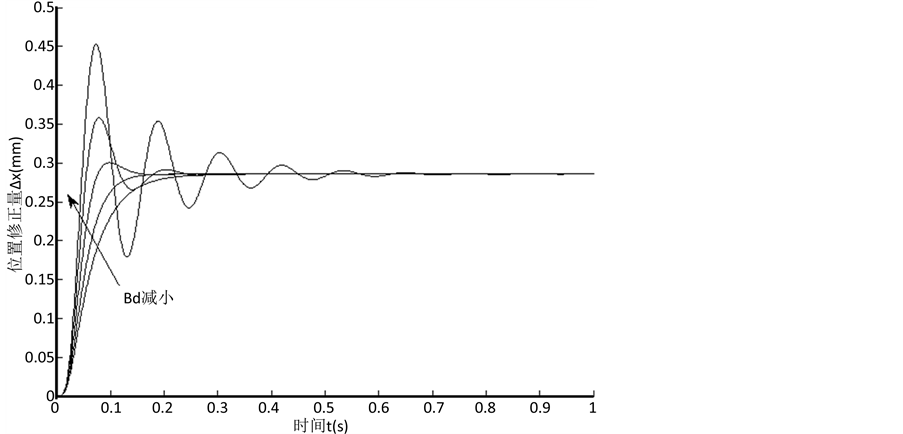
Figure 2. The influence of target damping
图2. 目标阻尼的影响
化而变化的过程，相接点必然向刚度减小的一方移动，以维持力平衡。
4. 基于阻抗控制的足力跟踪
4.1. 机器人腿部与地面接触等效模型
足端进入约束空间，即与地面接触后，足端与地面就组成了一个综合动态系统。本文采用柔性接触模型，将机器人与地面的接触模型简化为弹簧–阻尼系统。若只考虑机器人单腿沿竖直方向受力情况，可得到加入阻抗控制后的机器人单腿与地面的简化接触模型，如图4所示。其中
、
和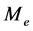
分别为环境的刚度特性、阻尼特性和惯性特性，
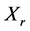为机器人末端的期望位置，
为机器人末端的实际位置，
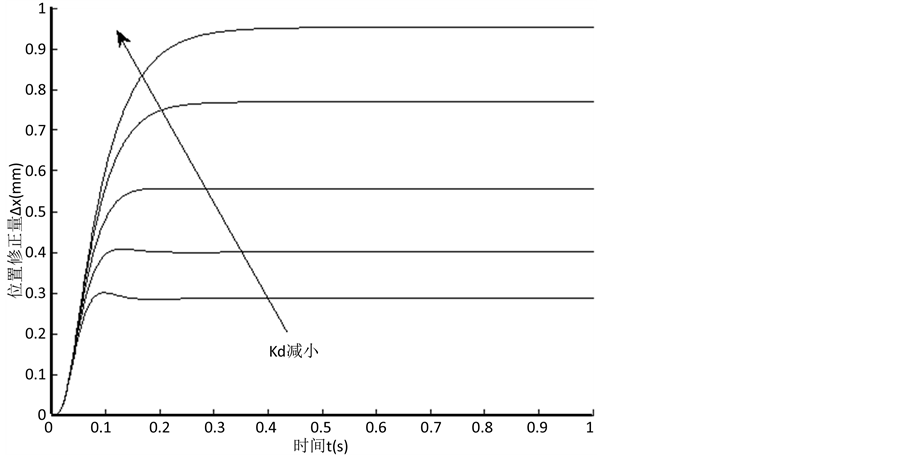
Figure 3. The influence of Target stiffness
图3. 目标刚度的影响
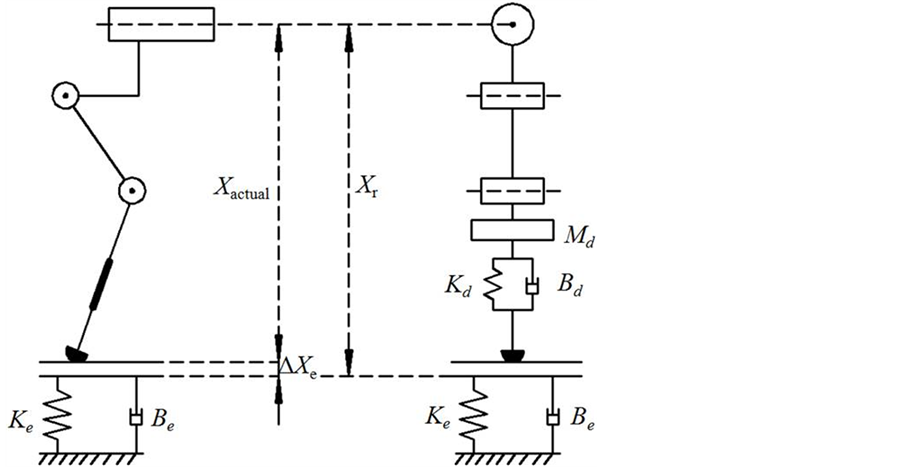
Figure 4. Simplified model of contact between leg and environmental
图4. 简化的腿与环境接触模型
为由于环境位置和机器人末端期望位置不同而产生的位置干扰，或理解为环境的微小形变量。
机器人末端与地面间的相互作用力可以用如下关系表示：
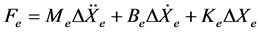(14)
式中，
机器人末端与地面之间的接触力。实际运动时，由于机器人足端的运动速度和加速度都比较小，故可以认为
，那么足端与环境的接触力模型可简化为:
(15)
其中，X为机器人足端在全局坐标系下的位置，Xe 为全局坐标系下环境的位置。
4.2. 阻抗控制下足力跟踪仿真研究
在该仿真模型的基础上，向机器人单腿运动控制系统中加入阻抗控制模型，即引入力闭环，可以实现对足力控制过程的仿真研究。控制系统中，选用如下阻抗模型：
(16)
对本文研究的四足机器人而言，基于位置的单腿阻抗控制结构框图如图5所示。按图搭建机器人单腿阻抗控制仿真模型，并给定环境刚度为Ke= 50 N/mm，环境干扰为∆Xe= 1 mm，期望力为Fr= 100 N。可以得出在阻抗控制下两个步态周期内足端与地面接触力的变化情况，如图6所示。图中，实线为阻抗控制策略下足端接触力的变化情况，点划线为不采用控制策略时足端接触力的变化情况，虚线为接触力的参考值。机器人单腿在第6秒时开始摆动，在约第7秒时与地面产生接触，应用阻抗控制策略后，足端与地面接触力的峰值下降至不采用控制策略时足端接触力的90%，且在单腿支撑地面的过程中，接触力值逐渐
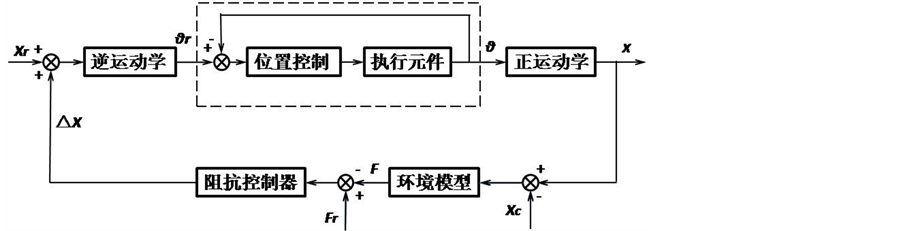
Figure 5. Block diagram of impedance control
图5. 阻抗控制框图
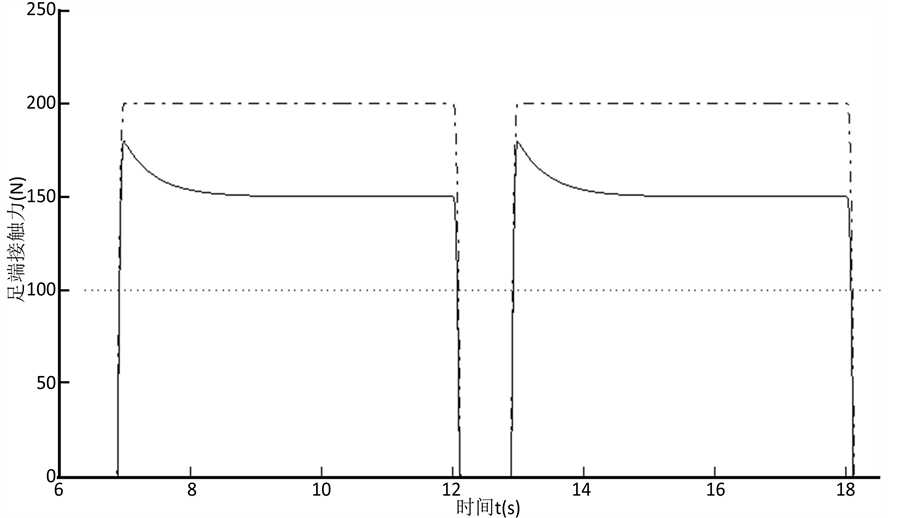
Figure 6. Changing of contact force at the foot end under impedance control
图6. 阻抗控制下足端接触力变化
减小，并逐渐稳定在150 N，该稳态值约为无控制策略时的75%。接触力的稳态误差为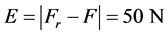
。
上述现象说明，通过选用合适的目标阻抗模型，基于位置的阻抗控制的确能够对参考力进行跟踪，并有效地减弱足端与环境接触时的力冲击。但是，单纯采用阻抗控制进行足力跟踪的控制系统存在稳态误差。
5. 结论
本文建立了基于位置的机器人单腿阻抗控制模型，完成了腿部关节的位置控制建模，并对阻抗控制器性能进行了分析。在建立了机器人腿部与地面接触等效模型的基础上，采用阻抗控制方法对机器人行走过程中足力进行控制，还完成了仿真分析。
基金项目
国家科技支撑计划, 2013BAH57F00。