1. 引言
微分求积法(differential quadrature method，简称DQM)最初由Richard Bellman等学者 [1] 提出，用于求解线性微分方程(组)的一种数值方法。该方法属于强离散形式的数值计算方法，计算逻辑简明，由于是全域高阶插值，所需节点数较少，计算效率较高。因此DQM在工程科学中得到广泛发展与应用。
微分求积法应用于求解全域连续性问题时高效准确，但实际中常常出现具有局域特殊性的问题，包括物理局域性(如集中或局域载荷等)和几何局域性(圆弧过度部位或不同材料界面等)问题。DQM和一般的数值计算方法相似，对于这类局域问题往往难于得到较好的计算效率和准确度。
一般来说，将全域划分为若干部分的单元化方式是处理局域问题行之有效的数值计算模式。这种方式虽然同样适用于微分求积法，但却明显的降低了后者高阶插值的计算效率。因此，本文基于作者对局域问题的研究 [2] ，提出了若干应用DQM处理局域问题的模式，进一步改善了DQM的应用性，丰富了DQM的应用模式。
2. 原理简介
2.1. 微分求积法
微分求积法的基本原理如下：若函数
在区间[a,b]上连续可微，则其在给定节点处的导数值可以表示为全域节点上的函数值的加权和。以光滑的一维函数
为例，函数的高阶导数可表示为
(1)
式中，
和
为域内节点，
为k阶导数的加权系数。
若基函数采用拉格朗日插值多项式，则一阶导数的权系数表达式如下：
(2)
其中，
。已知一阶权系数，各高阶权系数
可由下式推出：
(3)
综上所述，利用微分求积法可将函数各阶导数用域内各节点函数值的加权和表示，进而将描述物理问题的偏微分方程转化为以节点函数值为未知数的代数方程(组)求解。
2.2. 针对局域问题的改进型微分求积法——节点分布调节
由于微分求积法广泛采用拉格朗日插值函数，其阶次随节点数增多而升高，当节点数较多时计算稳定性降低乃至发散。另一方面，大量研究表明余弦节点分布因为更符合工程问题的物理性质，有助于求解的收敛和准确。因此，DQM有别于有限元法，增多节点数不一定是必要的，而调节节点分布使其符合具体问题的具体特征，才是节点分布合理性的关键。合理的节点分布有助于改善DQM求解局域问题时的收敛性和计算精度。
工程梁的局域问题(如多跨梁、弹簧约束等)并不罕见，在局部区域梁的变形(相比于其它部分)具有特殊性。基于文献 [2] 的研究，即以节点余弦分布为基础，靠近局部特殊区域的节点分布较密集，远离局部特殊区域的节点分布较稀疏，使节点有效分布更好的反映问题的局域特性 [3] 。依据上述原则，本节将梁分为两个大小不同的域，每个域的节点数相同，从而实现对局域节点分布的调整。
如图1所示，两端简支梁承受均布载荷q = 3 kN/m，材料弹性模量E = 100 GPa，泊松比
，梁长l = 1 m，梁横截面高b = 0.02 m，坐标轴x以梁的左端为原点，梁右端受弹簧约束，单位弹性约束刚度
，表1表示简支梁右端承受的不同弹簧约束刚度。
图2表示在不同弹簧约束刚度的情况下，随着节点数增多，利用调节节点分布的微分求积法计算梁最大挠度值的收敛过程以及与有限元值的对比。图中“0.575-0.425”表示梁非弹簧约束端区域长为0.575 m，弹簧约束端区域长0.425 m，其他类似。根据结果可以发现，除“0.6-0.4”情况之外，对于其他各种节点分布模式，改进的微分求积法计算得到的最大挠度值随着节点数的增加均表现出较好的收敛性。
2.3. 结合势能原理的微分求积法
为改善微分求积法处理局域问题所存在的一些缺陷，和势能原理相结合是一种显见的途径。这种结合依然在很大程度上保持了前者计算逻辑的简明，而嵌入势能原理后，原始问题本身所存在的物理/几何的局域性在一定程度上被“磨平”，其控制方程的微分阶次也降低了一阶，对数值计算也是有利的一面。因此，势能原理与微分求积法结合，有助于改善传统DQM的计算稳定性，扩大其应用范围以及提高计算准确性。
下面，以经典梁为例介绍DQM和势能原理结合的具体作法。
一般梁的总势能泛函 [4] 可表示为：
(4)
其中，EI为弯曲刚度，q为横向分布载荷密度。根据DQM原理 [5] ，可将总势能泛函离散成如下表达形式：
(5)
式中，
为[0,L]区间的高斯积分系数。最小势能原理可以表达为：
(6)
Figure 1. Simply supported beam with spring restraint on right
图1. 简支梁右端弹簧约束
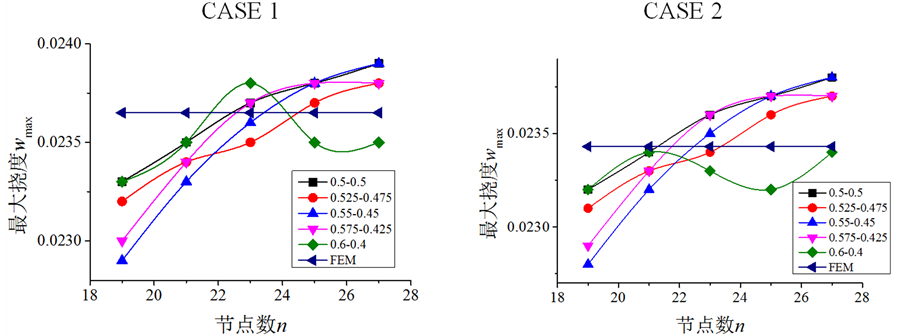
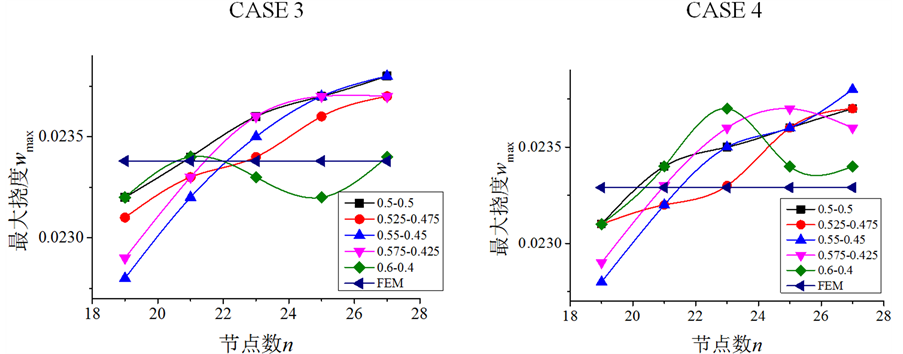
Figure 2. Curve: maximum deflection of beam
图2. 梁最大挠度收敛情况
Table 1. The spring’s stiffness value (unit: N∙m2)
表1. 弹簧刚度大小(单位：N∙m2)
进一步将边界条件利用方程替代法加到式(6)中，求解此线性方程组，可得问题解答。
2.3.1. 势能原理框架下的小波微分求积法
常规的微分求积法采用拉格朗日插值，由于全域插值，节点数增多插值阶次也随之增高，不利于数值计算的稳定和效率；不仅如此，即便是高阶的拉格朗日插值，对解决局域问题也难说是有力的方式。因此，本文采用具有良好局域近似特性的高斯小波尺度函数做为DQM的插值方式，并结合势能原理进行数值计算。
以图3所示简支梁为例，梁长l = 1 m，梁横截面高b = 0.02 m，梁由三段均质材料组成，各段材料弹性模量分别为
，
，
，泊松比
，q = 3 kN/m，坐标轴x以梁的左端为原点。
图4表示将势能原理与小波-DQM结合后，计算的变弹性模量梁的最大挠度收敛情况以及与有限元结果的对比。图4表明本文所采用的方法收敛较快，并且与有限元结果十分接近。有限元处理此类问题时通常要建立三种不同的单元，需要考虑内部连续条件，但利用DQM求解此类问题并不需要。
2.3.2. 非贯穿线载荷作用下的对边简–固支撑板
如图5所示，工程板一对边简支、另一对边固支，材料弹性模量E = 100 GPa，泊松比
，板厚度h = 0.005 m，板长a = 1 m，宽b = 1 m，线载荷q = 396.8 N/m。表2列举了工程板的边界条件和载荷作用位置的不同情况，其中，边界条件“x”表示固支位置选取在x = 0与x = 1的位置，“y”亦类似。线载荷位置标识参看图5。
计算结果如图6所示，图中红线表示采用拉格朗日插值的微分求积法所得到的数值计算收敛情况；蓝线表示选取高斯小波尺度函数作为微分求积法的插值函数并结合势能原理计算得到的结果。通过观察发现在收敛速度与准确性上，选取高斯小波尺度函数作为插值函数并结合势能原理的微分求积法取得了较好的计算效果。
3. 与势能原理相结合的微分求积法求解压电智能梁问题的应用
压电材料作为一种智能材料应用较为广泛，将压电材料膜片粘附在结构表面或者嵌入结构内部，利用材料正、逆压电效应作为感应器和驱动器，与外界控制电路一起来贯彻变形与实施变形控制，是压电材料应用的主要形式。
3.1. 压电材料及其本构关系简介
压电材料受到外力作用会发生变形，即压电材料的力学行为，还会在压电材料表面产生电荷形成电
Figure 3. Schematic diagram of variable elastic modulus beam
图3. 变弹性模量梁示意图
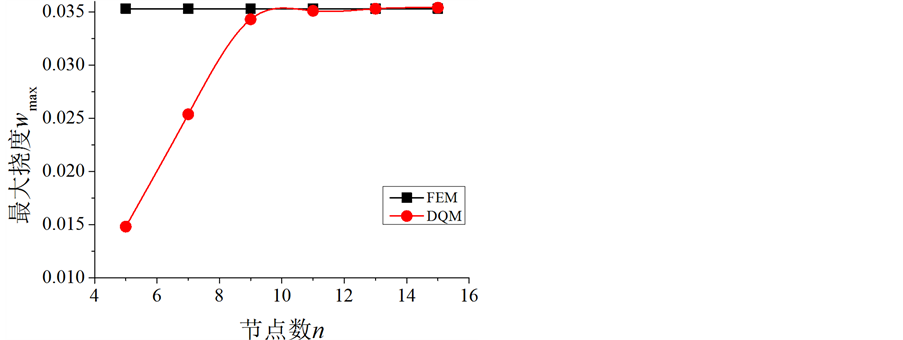
Figure 4. Curve: maximum deflection of beam
图4. 梁最大挠度收敛情况
Table 2. The boundary condition and the location of non-through linear load
表2. 边界条件及线载荷作用位置
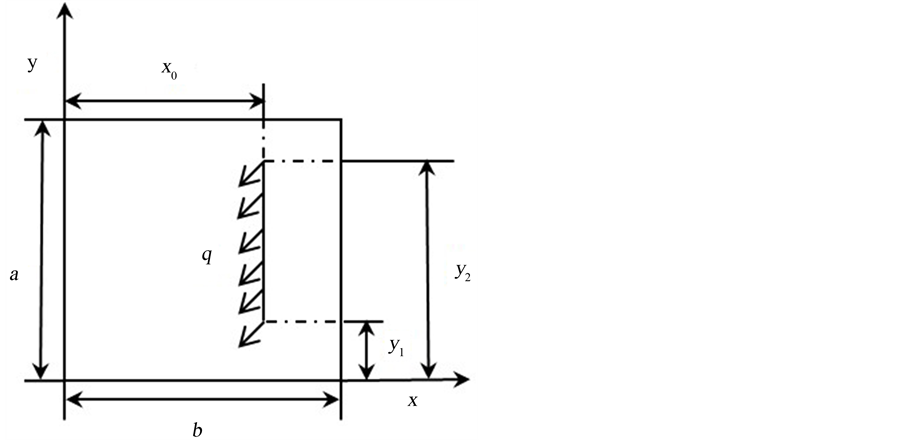
Figure 5. Plate of non-through liner load
图5. 非贯穿线载荷作用板
位移，即压电材料的电学行为；压电材料在外加电场中也会发生机械变形，进而产生电应变。综合压电材料的力学行为和电学行为即可得到压电材料本构关系表达式。
3.1.1. 压电材料的正压电效应
(7)
式中，D是压电材料的电位移；
是压电应变常数，第一个下标表示所产生的电位移方向，第二个下标表示所受应力的方向；
是介电常数，单位为N/m，第一个下标表示电位移的方向，第二个下标表示电场强度的方向，上标
表示材料应力为常数时的介电常数。式(7)表明压电材料的电位移由施加给压电材料的应力与电场强度两部分的影响组成，反映的是压电材料将机械能转换为电能的关系。
3.1.2. 压电材料的逆压电效应
(8)
式中，E为外加电场；
称为柔度系数，单位为N/m2，第一个下标表示压材料产生应变的方向，第二个下标表示所受应力的方向，其上标E表示外加电场为常数时的柔度系数；
也称为压电应变常数，但含义有所不同：第一个下标表示外加电场的方向，第二个下标表示由其产生的应变的方向。式(8)表明压电材料的应变是由其所受到的应力产生的应变和施加给压电材料的电场导致其产生的应变之和，反映了压电材料将电能转换为机械能的关系。
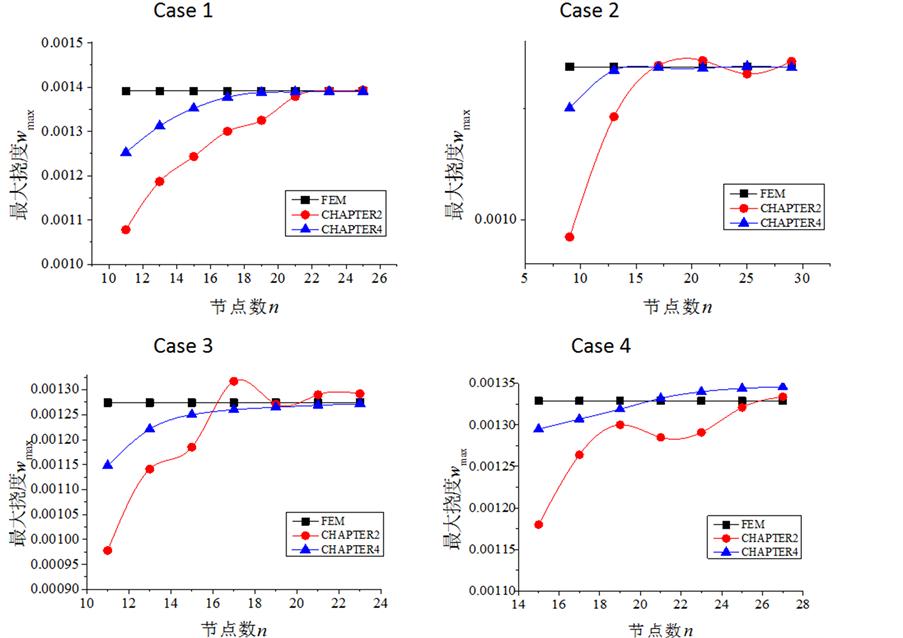
Figure 6. Curve: maximum deflection of plate
图6. 板最大挠度收敛情况
3.1.3. 极化处理后的压电材料
实际使用的压电材料在生产过程中必须对其进行极化处理才会具有压电特性。极化方向为x轴(参见图7)的压电材料极化处理后，其压电应力常数矩阵中的元素除
，
以及
三个独立的压电应力常数外，其他常数均为0；介电常数也只剩下
和
两个独立的介电常数，其它分量均为0。
尽管压电材料的压电应变关系是三维的，压电常数很多，但通常情况下只是使用其中一个方向上的压电应变关系。本文使用的压电材料，其长度方向为其极化方向，左右表面分别为其正负电极，利用压电材料的逆压电效应，即向压电材料输入电压后产生力的作用，假设不计压电作动元件的应力效应，简化了的逆压电方程为：
(9)
则压电智能梁弯曲问题的力电耦合本构方程(9)用矩阵表达如下
(10)
3.2. 弯曲作用下的压电智能梁
考虑两端简支压电智能梁 [6] ，坐标轴x以梁的左端为原点，如图7所示，承受均布载荷q = 1 kN/m，梁长l = 1 m，高
，宽b = 0.01 m，梁的材料弹性模量为E = 100 GPa，泊松比
；其上表面粘贴作为作动器的矩形压电片，厚为
，长为
(参见表3)，厚度均匀且压电片与梁等宽度；
Table 3. Number of nodes of simply supported beam and the location of piezoelectric patch
表3. 两端简支压电智能梁的结点个数及压电片位置
Figure 7. Piezoelectric smart beam of uniform load
图7. 均布载荷压电智能梁
压电片与梁粘贴良好，忽略其对梁弯曲的影响，并假设压电片轴向应力随厚度不变，即对梁的作用可以等效为在梁上下表面处的一对平衡力偶。
在输入电压作用下，根据逆压电效应，压电驱动器的输入电场强度、等效应力、端点等效力矩分别为：
(11)
(12)
(13)
结合式(11)~(13)可得影响梁弯曲挠度的等效力矩表达式为：
(14)
式中，U为输入电压；Ka为压电耦合系数，表达式为：
(15)
3.3. 压电梁具体实例计算结果与ABAQUS仿真分析
本文采用的压电材料为PZT-4(锆钛酸铅固溶体),其材料参数为：
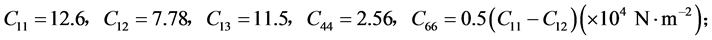
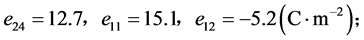
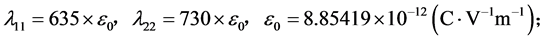
压电片位置
和
情况及计算结果如表3所示。
压电作动器在输入电压的作用下对梁产生的力矩可由式(14)求得，由结合变分原理的微分求积法，可求得压电智能梁在均布载荷下的挠度，计算结果与有限元结果对比，准确性较好。上述方式进一步拓展了DQM的应用范围。
4. 结论
本文针对工程问题中的一些局域问题，在应用微分求积法时，结合了具体的节点分布改进方式、插值方式以及势能原理的计算模式，改进后的DQM不仅能够保证计算结果的收敛性与精确性，还能够降低DQM的插值阶次，对于改进DQM具有重要的意义，也有助于提高DQM的计算效率，拓展了微分求积法在具有局域特殊性问题上的适用性。