1. 引言
碰撞是物体间相互作用的一种形式。接触碰撞动力学是研究在碰撞作用下，物体间相互作用规律和物质运动规律的科学。如何建立正确有效的接触碰撞模型是解决接触碰撞动力学问题的关键，国内外学者对于接触碰撞问题做了一系列研究，目前接触碰撞动力学分析方法一般分为三种 [1] [2] [3] ：碰撞瞬态模型方法、连续接触力方法、有限元方法。碰撞瞬态模型方法属于离散方法，假定接触碰撞时间非常短且刚体构型未发生改变，忽略碰撞过程，仅研究碰撞前和碰撞后两个阶段。连续接触力方法和有限元方法属于连续接触方法，三种方法各有特点。
碰撞瞬态模型方法是基于经典碰撞模型 [4] 的，经典的碰撞理论包含一系列简化假定，这一系列假定是否可用，还需要根据具体情况分析。这些假定有：碰撞瞬态假定、局部性假定、法向碰撞规律不受切向运动的影响等，研究这些假定的适用范围有重要意义。这些假定在探究球状近刚性物体碰撞时是比较适用的，但是推广到研究含摩擦的多刚体系统碰撞问题就必须进行修正 [5] 。
连续接触力模型，将碰撞过程看成是一个有限时间的接触碰撞力的作用过程，利用连续力与位移的关系模型来处理碰撞物体之间的关系，当实际物体形状复杂时，很难得到连续力与位移的关系 [6] 。
有限元柔性模型，此种方法更接近于实际的碰撞接触过程，但是其计算过程很耗时间。有限元方法具有通用性，但是碰撞的物体的形状比较复杂和个数比较多时，用有限元方法计算耗时将是巨大的 [7] 。
本文基于连续接触力方法建立接触碰撞模型，针对均质杆与地面斜碰撞的经典例子，对碰撞过程进行动力学模拟。研究不同的初始位形、初始速度及摩擦系数下系统运动的变化规律及相应的滑动模式，并通过该模型，展示了碰撞过程中复杂的切向滑动模式，为碰撞模型的正确选择提供参考依据。
2. 刚体平面运动接触碰撞模型
2.1. 法向接触力模型
当接触点的相对距离
时(
为物体之间相互嵌入的深度，
为相对速度)，碰撞将会发生，进入碰撞计算，计算方程中力的一项需要增加接触力。
取法向接触力模型 [1] 为：
(1)
公式(1)对弹性碰撞是成立的，但是对于非弹性碰撞，由于能量的耗损，碰撞后变形不能够恢复，在恢复阶段会出现
时
，该模型体现了碰撞过程中弹性压缩、恢复及能量损耗的特征。
2.2. 切向摩擦模型
在接触碰撞的过程中如果两个接触物体有相对滑动，在接触点会有切向速度，切线方向会受到摩擦力的作用。
当没有相对运动时，如果有相对运动趋势，此时物体所受的是静摩擦力。一般当沿接触面切向外力小于最大静摩擦力时，静摩擦力大小等于这个切向外力，方向相反。当外力大于或等于最大静摩擦力时，物体发生相对运动此时受到的是动摩擦即Coulomb摩擦，方向与运动方向相反，取下列的切向摩擦模型：
(2)
其中，
是沿接触面切线方向的外力，
是最大静摩擦力，
是摩擦力，
是相对滑动速度，
是库仑摩擦力，
，
是摩擦系数，
是法向力，
是符号函数。
3. 匀质杆件与地面接触碰撞模型
如图1，匀质细杆
长
，质量为
与地面夹角为
，以平行于自身的速度
与地面发生接触碰撞,接触点为
，假设绕质心
的转角为
，角速度为
，以顺时针旋转为正。碰撞前匀质细杆只受重力。
由细杆几何关系可知两个端点与质心的关系为：
(3)
(4)
在匀质细杆与地面接触碰撞的过程中，接触点在法向的变形为
：
(5)
依据对匀质细杆与地面进行接触识别，此处我们假设接触点就是
，当杆与地面发生碰撞时
，且此时
，到变形最大时，
，这一过程是压缩阶段；在碰撞即将结束时
，
，法向速度由0逐渐增大的阶段是接触碰撞的恢复阶段。对于碰撞结束时的判断条件只适用于弹性碰撞，如果接触碰撞不是弹性的，那么接触点的变形不能恢复到碰撞前的状态，此时判断碰撞是否完成的依据是接触力是否为零。
在碰撞过程中，匀质细杆受到重力、摩擦力和接触力，当接触碰撞开始时，杆件质心的平衡微分方程为：
(6)
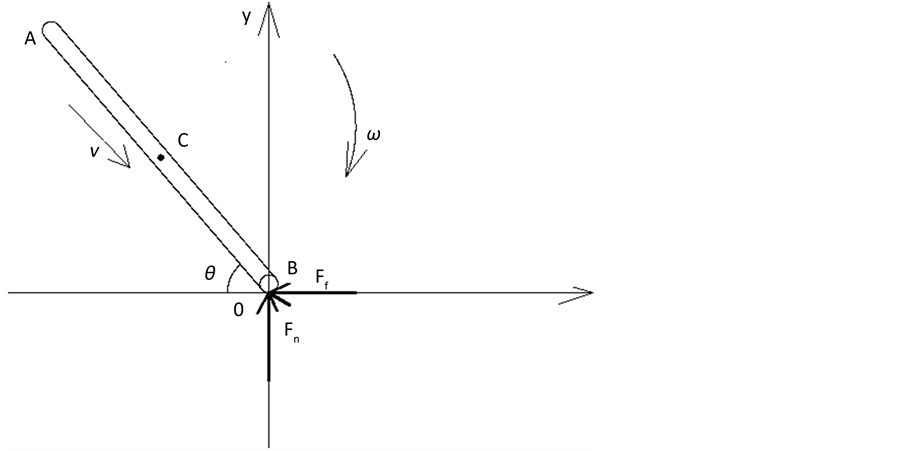
Figure 1. Sketch map of the collision between the uniform thin rod and the ground
图1. 匀质细杆与地面碰撞示意图
当
时
1) 假设
，则摩擦力可能为静摩擦力，切向的运动微分方程不满足，则得到新的平衡微分方程：
(7)
通过计算可以得出受到摩擦力大小，如果实际摩擦力始终小于最大静摩擦力，碰撞结束前接触点处于粘滞状态。若求得实际摩擦力大于最大静摩擦力，则接触点继续滑动。如果接触点继续滑动，则摩擦力变为滑动摩擦力，重新建立新的运动微分方程开始下一步的计算。
2) 当
时，根据加速度的方向，可以判断摩擦力的方向，此时运动微分方程依然满足公式（6），但是其摩擦力的方向随速度的改变发生改变。
4. 数值算例
匀质细杆长度
，底面半径
，质量为
，杆件与接触地面的弹性模量和泊松比相同，弹性模量
，泊松比
，摩擦系数
，假设碰撞时接触点的坐标
，平行与匀质细杆的初始速度为
，接触点对质心的转动惯量
，以绕质心顺时针转动为正。
4.1. 初始位形及切向摩擦对法向接触力的影响
图2是在杆件初始位形不同时，接触力随时间的变化曲线。初始夹角的改变会引起质心初始坐标以及质心在坐标轴方向的初始速度分量的改变。从图线中可以看出，碰撞开始时，杆件和地面的夹角越大，接触力的峰值越大，接触力单位时间的变化速度越快，接触碰撞的作用时间越短。
图3是不同摩擦系数下法向接触力的变化曲线，由图可以看出，随着摩擦系数的不断增大，相同时
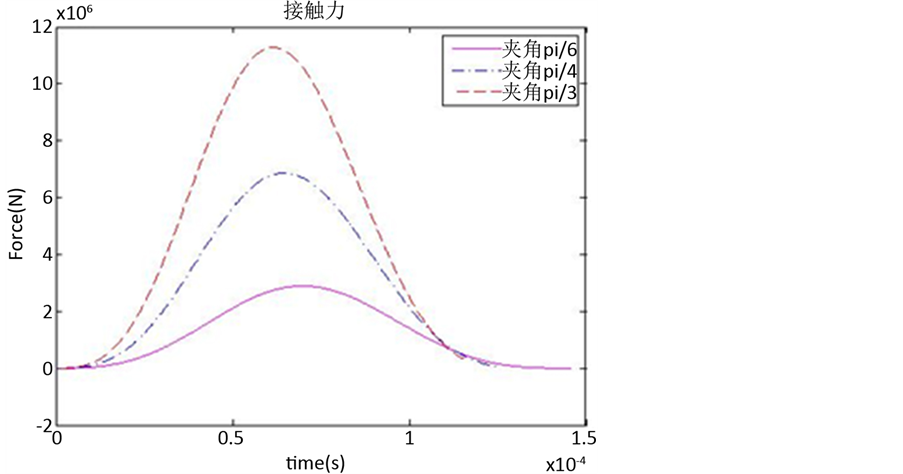
Figure 2. Curves of normal contact force under different initial configurations
图2. 不同初始位形下的法向接触力变化曲线
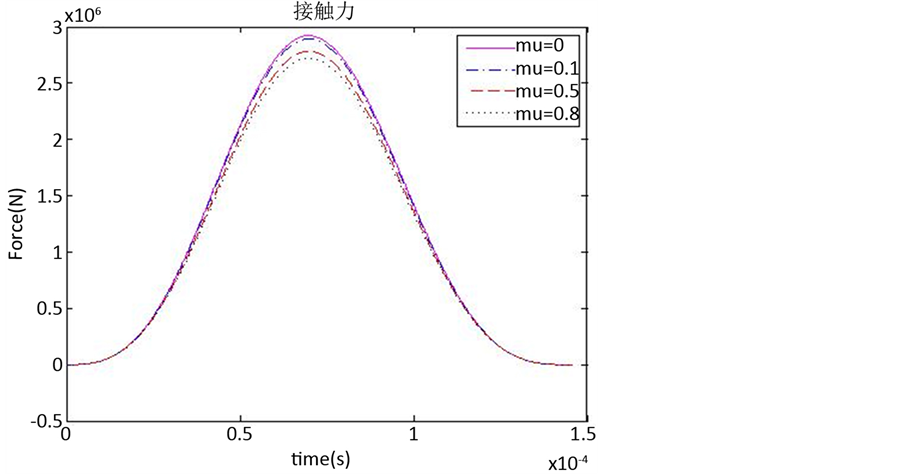
Figure 3. Normal contact force curve of different friction coefficient method
图3. 不同摩擦系数下法向接触力变化曲线
刻，接触力的值是在逐渐减小的，且摩擦系数越大，接触力的峰值会越小。因此可以通过增大摩擦力来减小法向的接触力。
通过计算可以得到：
时，碰撞时间为
；
，碰撞时间为
；
，碰撞时间为
；
，碰撞时间为
。接触力的作用时间会随着摩擦系数的增大而变长。
由于初始条件的设置，接触点的切向速度在碰撞过程中未减小到0，因此不会出现粘滞或者反向滑动的情况，但可以计算得到，随着摩擦系数的增大，碰撞结束时接触点的切向速度是减小的。
4.2. 碰撞过程中切向滑动模式的验证
取下列参数：质心
，杆与地面的夹角
，初始角速度
，以顺时针转动为正。
通过计算可以得到接触点切向速度如图4示，当
时，接触点的切向速度变为0，此时法向碰撞力不为零，处于恢复阶段，碰撞并没有结束。
继续计算可以得到每一时刻实际受到的摩擦力与最大摩擦力的关系，如图5所示，到碰撞结束，杆件受到实际的摩擦力始终小于最大静摩擦力，因此碰撞结束前杆件一直处于粘滞状态。
算例很好地验证了在所设定的初始条件下，碰撞过程中滑动模式的变化情况：开始滑动而后在恢复阶段发生粘滞一直到碰撞结束。
5. 数值算例
本文采用连续接触力的方法建立接触碰撞模型。针对均质杆与地面斜碰撞的经典例子，对碰撞过程进行动力学模拟。研究不同的初始位形、初始速度及摩擦系数下系统运动的变化规律及相应的滑动模式，得到以下结论：
初始位形不同，法向接触力会有不同的变化规律，通常的碰撞恢复系数常数型假设在此种情况下并不成立；
摩擦系数不同，法向接触力会受到影响，体现了切向运动对法向运动的影响，该影响在瞬时碰撞模型中被忽略；
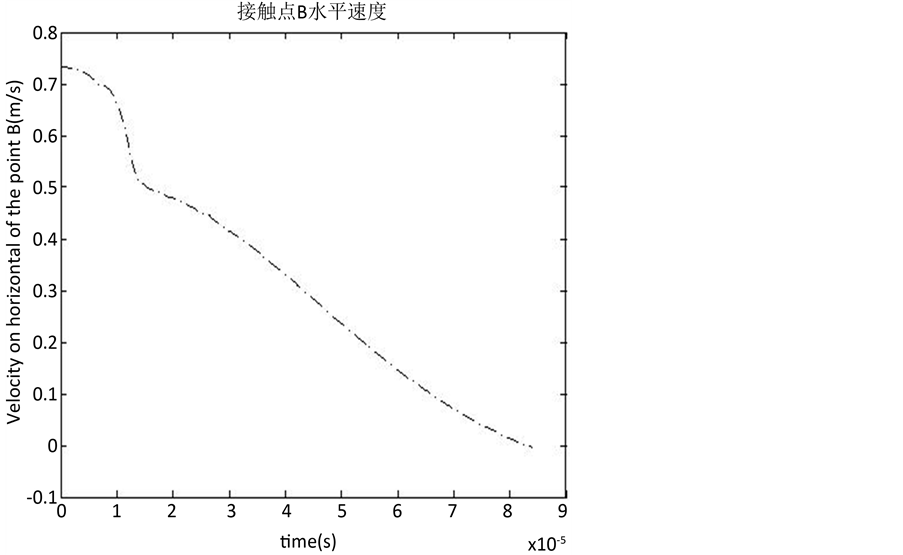
Figure 4. Tangential velocity of contact point in contact impact process
图4. 接触碰撞过程接触点的切向速度
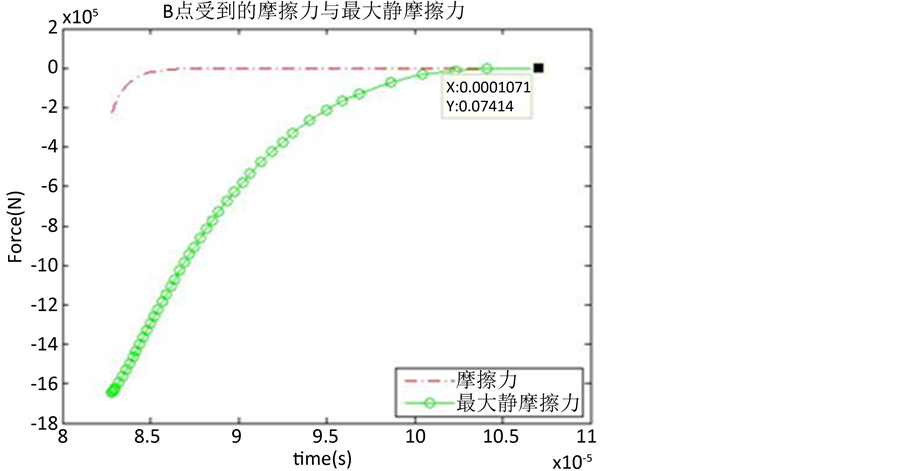
Figure 5. Actual friction and maximum static friction
图5. 实际受到摩擦力与最大静摩擦力
验证了碰撞过程中复杂的切向滑动模式的存在。
碰撞瞬态模型方法因其模型简单，计算方便在目前多体系统的动力学与控制问题中仍然得到广泛的应用，但其经典模型的合理性及精确性也一直是人们关注的热点，本文基于连续接触力的方法所得到的结论有助于碰撞模型的选择及建立。
基金项目
国家自然科学基金(11272167)。