摘要:
设Bm 是m维复欧式空间Cm的单位球,本文利用Bm×Bn的Bergman度量方阵和实多项式1-||z||2 的不可约性,重新得到了单位球的乘积Bm×Bn的全纯自同构群Aut(Bm×Bn)。
Abstract:
Let Bm be the unit ball in the m dimensional complex Euclidean space Cm, in this paper using the Bergman metric of Bm×Bn and irreducibility of a polynomial 1-||z||2 , we obtain the holo-morphic automorphism group of a product Bm×Bn of the unit balls again.
1. 引言
设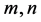 为正整数,
为正整数, 维复欧氏空间
维复欧氏空间 的单位球
的单位球 和单位球
和单位球 与
与 的乘积分别定义为
的乘积分别定义为
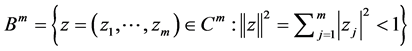 , (1.1)
, (1.1)
 , (1.2)
, (1.2)
这里 为域
为域 的全纯自同构群,即
的全纯自同构群,即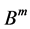 的双全纯自映射按映射符合运算构成的群,同样
的双全纯自映射按映射符合运算构成的群,同样 表示域
表示域 的全纯自同构群。
的全纯自同构群。
对 的自同构群,有以下熟知的结果,其证明细节可参考 [1] 和 [2] 。
的自同构群,有以下熟知的结果,其证明细节可参考 [1] 和 [2] 。
引理1.1设 ,则存在唯一的
,则存在唯一的 和唯一的
和唯一的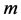 阶酉矩阵
阶酉矩阵 ,使得
,使得
 (1.3)
(1.3)
其中
 , (1.4)
, (1.4)
这里符号 表示
表示 阶单位矩阵,
阶单位矩阵,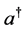 表示
表示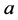 的共轭转置。
的共轭转置。
对单位球的乘积的自同构群有许多研究,如 [3] 和 [4] ,在本文中我们使用 [5] 和 [6] 的方法,即用Bergman核和Bergman度量方阵在全纯自同构下的变换公式重新证明了以下定理1.2,在证明中还使用了实多项式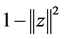 在实数域上的多元多项式环上是不可约这一性质。
在实数域上的多元多项式环上是不可约这一性质。
定理1.2设 ,则存在
,则存在 ,
, ,使得
,使得
i) 当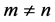 时,有
时,有
 , (1.5)
, (1.5)
即
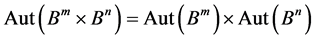 .
.
ii) 当 时,有
时,有
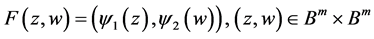 , (1.6)
, (1.6)
或
 , (1.7)
, (1.7)
即
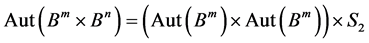 ,
,
这里 表示二阶置换群。
表示二阶置换群。
2. 定理1.2的证明
在定理1.2的证明过程中,我们要用到 的Bergman核以及Bergman度量方阵,为方便我们先叙述这些结论,其证明细节可参考 [2] , [7] 和 [8] 。
的Bergman核以及Bergman度量方阵,为方便我们先叙述这些结论,其证明细节可参考 [2] , [7] 和 [8] 。
引理2.1单位球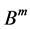 的Bergman核可表示为
的Bergman核可表示为
 ,
,
于是Bergman度量方阵为
 ,
,
这里符号 表示矩阵
表示矩阵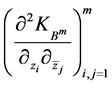 。
。
定理1.2的证明
令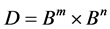 ,设
,设 是
是 到
到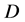 的全纯自同构,则
的全纯自同构,则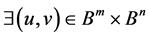 ,使得
,使得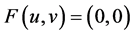 。仿(1.4)构造
。仿(1.4)构造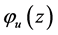 和
和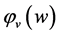 ,则
,则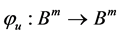 是
是 的自同构,
的自同构, 是
是 的自同构。定义
的自同构。定义
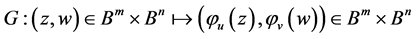 ,
,
则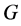 为
为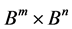 的自同构,且
的自同构,且 。
。
定义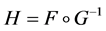 ,则
,则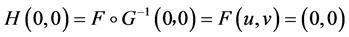 ,这表明
,这表明 是把
是把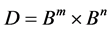 的原点映为原点的自同构。
的原点映为原点的自同构。
由Cartan定理得 为线性可逆映射,即
为线性可逆映射,即
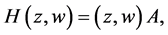
其中
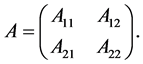
又由Bergman核变换公式 [8]
 ,
,
以及 得
得
 .
.
这表明 ,这里
,这里 表示A的行列式,于是
表示A的行列式,于是
 , (2.1)
, (2.1)
这里 。
。
令 ,因
,因 的Bergman核为
的Bergman核为
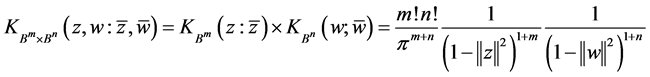 . (2.2)
. (2.2)
于是得
 . (2.3)
. (2.3)
由(2.2)有
 ,
,
又因
 ,
,
以及由引理2.1得
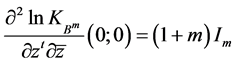 ,
,
这里 表示矩阵
表示矩阵 的共轭转置。
的共轭转置。
所以当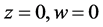 时,有
时,有
 . (2.4)
. (2.4)
根据(2.3)得
 . (2.5)
. (2.5)
现对等式(2.5)分三种情形讨论。
i) 设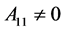 ,令
,令 ,则
,则
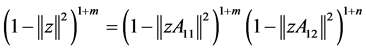 。
。
因 是不可约实多项式,而
是不可约实多项式,而 为非平凡多项式,以及实数域上多项式环为唯一因子整环,故
为非平凡多项式,以及实数域上多项式环为唯一因子整环,故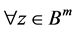 有
有 ,即
,即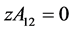 ,因此有
,因此有 。
。
又由

得
 ,
,
即
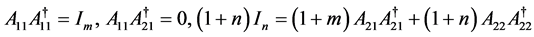 .
.
这表明 为
为 阶酉矩阵,并且
阶酉矩阵,并且
 .
.
此时
 ,
,
其中 为酉矩阵。
为酉矩阵。
ii) 当 时,仿i)讨论仍有
时,仿i)讨论仍有

其中 为酉矩阵。
为酉矩阵。
iii) 当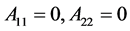 时,有
时,有

根据(2.4)式得
 ,
,
即
 .
.
因 分别
分别 型矩阵,由上式有
型矩阵,由上式有 且
且 ,得
,得 ,于是
,于是
 ,
,
这表明 为同阶酉矩阵。
为同阶酉矩阵。
综上所述,有以下结论。
1) 当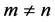 时,
时,
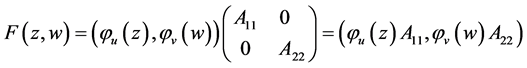 ,
,
这里 ,
, 分别为
分别为 阶,
阶, 阶酉矩阵,令
阶酉矩阵,令

则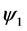 为
为 到
到 的自同构,
的自同构,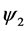 为
为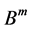 到
到 的自同构,并且
的自同构,并且

这表明
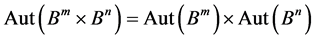
2) 当 时,
时,

或
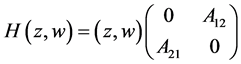
这里 为
为 阶酉矩阵,此时
阶酉矩阵,此时
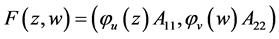
或
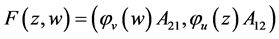
这表明

并且

基金项目
国家大学生创新创业训练计划项目(No: 201610649047);乐山师范学院科研项目(No: Z1513)。
*通讯作者。